Содержание
- 2. Любое целое n >1 может быть представлено единственным образом с точностью до порядка сомножителей как произведение
- 3. Наибольший общий делитель чисел a и b, обозначаемый как НОД (a,b) или просто (a,b), – это
- 4. Опишем алгоритм Евклида для нахождения НОД (a,b). Введем обозначения: qi – частное; ri – остаток. Тогда
- 5. Остановка гарантируется, поскольку остатки ri от делений образуют строго убывающую последовательность натуральных чисел. Таким образом, rn
- 6. Алгоритм Евклида для вычисления наибольшего общего делителя begin g[0]: = b; g[1]: = a; i :
- 7. Вычисление обратного элемента по заданному модулю Если целые числа а и n взаимно просты, то существует
- 8. Расширенный алгоритм Евклида При заданных неотрицательных целых числах a и b этот алгоритм определяет вектор (u1,
- 9. Для вычисления обратной величины a–1 (mod n) используется частный режим работы расширенного алгоритма Евклида, при котором
- 10. Шаги алгоритма: 1. Начальная установка. Установить (u1, u2, u3) : = (0, 1, n), (v1, v2,
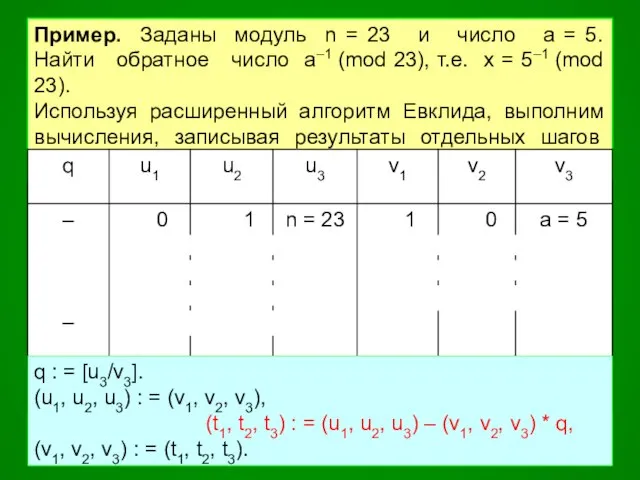
- 11. Пример. Заданы модуль n = 23 и число a = 5. Найти обратное число a–1 (mod
- 12. При u3 =1, u1 = –9, u2 = 2 (a * u1 + n * u2
- 13. Малая теорема Ферма Если m – простое число, и a не кратно m ,то малая теорема
- 14. Функция Эйлера Приведенной системой вычетов по модулю п называют подмножество полной системы вычетов, члены которого взаимно
- 15. Функция Эйлера, которую иногда называют функцией «фи» Эйлера и записывают как φ(п), указывает число элементов в
- 16. В соответствии с обобщением Эйлера малой теоремы Ферма, если НОД(а,п) = 1,то: Теперь нетрудно вычислить а-1
- 17. Основные способы нахождения обратных величин a–1 (mod n). Проверить поочередно значения 1, 2, ..., n –
- 18. 2. Если известна функция Эйлера ϕ(n), то можно вычислить a–1 (mod n) ≡ aϕ(n)–1 (mod n),
- 19. Если функция Эйлера ϕ(n) не известна, можно использовать расширенный алгоритм Евклида. n=23 a=5 ExtendedGCD[n,a] {1,{2,-9}} u3
- 20. Для решения более сложных сравнений a * x ≡ b (mod n), т.е. b ≠1, x
- 22. Теория сложности Теория сложности обеспечивает методологию анализа вычислительной сложности различных криптографических методов и алгоритмов. Она сравнивает
- 23. Большие числа
- 24. Большие числа
- 25. Большие числа
- 26. Большие числа
- 27. Большие числа
- 28. Проблемы начнутся, когда мы учтём квантовые явления. Главный результат применения квантовой теории к чёрной дыре состоит
- 29. В рамках классической (неквантовой) теории гравитации чёрная дыра — объект неуничтожимый. Она может только расти, но
- 30. Рисунок художника: аккреционный диск горячей постоянной плазмы, вращающийся вокруг чёрной дыры
- 31. Сложность алгоритмов Сложность алгоритма определяется вычислительными мощностями, необходимыми для его выполнения. Вычислительная сложность алгоритма часто измеряется
- 32. Вычислительная сложность алгоритма выражается с помощью нотации "О большого", т.е описывается порядком величины вычислительной сложности. Это
- 33. Алгоритмы классифицируются в соответствии с их временной или пространственной сложностью. Алгоритм называют постоянным, если его сложность
- 34. Алгоритмы, сложность которых равна О(t f(n)), где t - константа, большая, чем 1, a f(n) -
- 35. На практике, самые сильные утверждения, которые могут быть сделаны при текущем состоянии теории вычислительной сложности, имеют
- 36. При условии, что единицей времени для нашего компьютера является микросекунда, компьютер может выполнить постоянный алгоритм за
- 37. Взглянем на проблему вскрытия алгоритма шифрования грубой силой. Временная сложность такого вскрытия пропорциональна количеству возможных ключей,
- 38. Сложность проблем Теория сложности также классифицирует и сложность самих проблем, а не только сложность конкретных алгоритмов
- 39. В нашем варианте машина Тьюринга состоит из управляющего устройства с конечным числам состояний (finite-state control unit),
- 40. Каждая головка имеет доступ к своей ленте и может перемещаться вдоль нее влево и вправо. Каждая
- 41. Каждый символ занимает одну ячейку, а оставшиеся ячейки ленты, расположенные справа, остаются пустыми (blank). Описанная выше
- 42. В каждый момент времени только одна из головок имеет доступ к своей ленте. Операция доступа головки
- 43. Если машина начинает работу с начального состояния, последовательно выполняет такты, сканирует исходную строку и завершает работу,
- 44. Исходные данные, распознаваемые машиной Тьюринга, называются предложением (instance) распознаваемого языка (language). Для каждой конкретной задачи машину
- 45. Количество тактов Тм, которые машина Тьюринга М должна выполнить при распознавании исходной строки, называется продолжительностью работы
- 46. Легко видеть, что Тм(п) ≥ п. Кроме временных ограничений, машина М имеет ограничения памяти SM, представляющие
- 47. Если машина начинает работу с начального состояния, последовательно выполняет такты, сканирует исходную строку и завершает работу,
- 48. Детерминированное полиномиальное время Функция р(п) является полиномиальной по целому аргументу п, если она имеет вид: где
- 49. Определение : Класс . Символом обозначается класс языков, имеющих следующие характеристики. Язык L принадлежит классу
- 50. Языки, распознаваемые за полиномиальное время, считаются "всегда простыми", а полиномиальные машины Тьюринга — "всегда эффективными". Рассмотрим
- 51. В работах, посвященных теории вычислительной сложности, задача считается решенной, только если любой экземпляр данной задачи можно
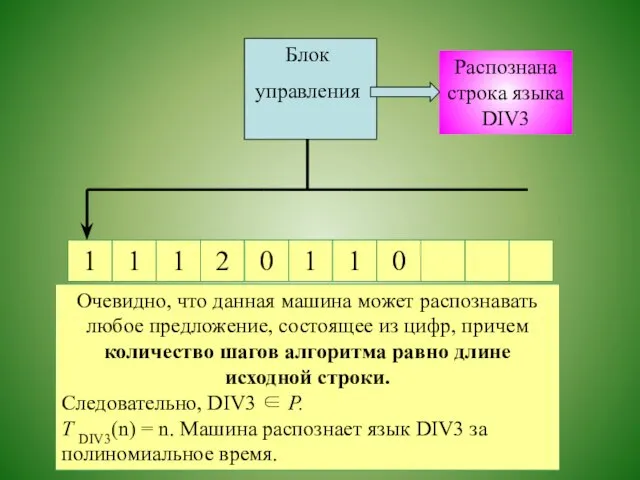
- 52. Пример - язык DIV3 Пусть DIV3 — множество неотрицательных целых чисел, кратных трем. Покажем, что DIV3
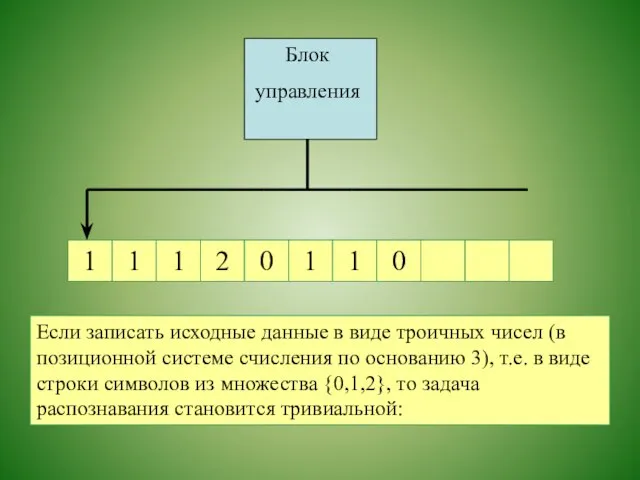
- 53. 1 1 1 1 1 2 0 0 Блок управления Если записать исходные данные в виде
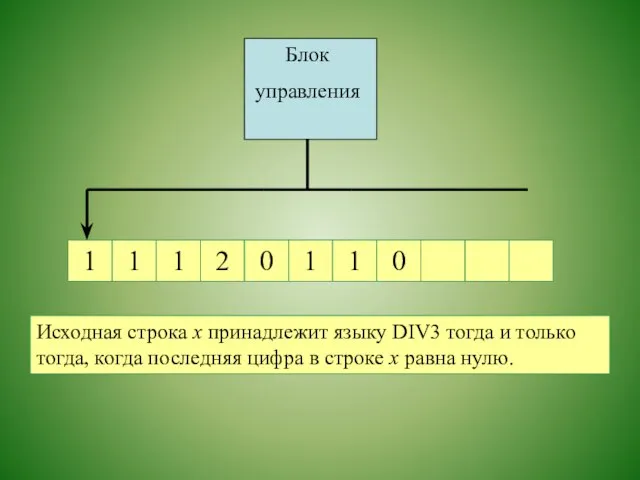
- 54. 1 1 1 1 1 2 0 0 Блок управления Исходная строка х принадлежит языку DIV3
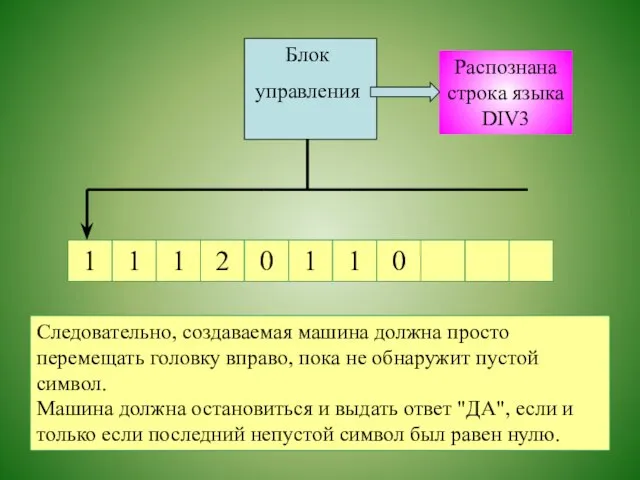
- 55. 1 1 1 1 1 2 0 0 Блок управления Распознана строка языка DIV3 Следовательно, создаваемая
- 56. 1 1 1 1 1 2 0 0 Блок управления Распознана строка языка DIV3 Очевидно, что
- 57. Полиномиальные вычислительные задачи По определению класс является классом языков, распознаваемых за полиномиальное время. Задача распознавания
- 58. Вычислительное устройство, имеющее неймановскую архитектуру (иначе говоря, всем известную современную компьютерную архитектуру), состоит из счетчика, памяти
- 59. Можно доказать ,что каждую микрокоманду из указанного выше набора, можно имитировать на машине Тьюринга за полиномиальное
- 60. -символика (order notation) Символом (f(n)) обозначается функция g(п), для которой существует константа с > 0 и
- 61. Теорема. Наибольший общий делитель gcd(a, b) можно вычислить с помощью не более чем 2mах(|а|, |b|) операций
- 62. Таким образом, временная сложность алгоритма вычисления наибольшего общего делителя ( при условии a > b )
- 63. В рамках модели поразрядных вычислений на сложение и вычитание двух целых чисел i и j затрачиваются
- 64. Поразрядные оценки сложности основных операций в модулярной арифметике
- 65. Недетерминированное полиномиальное время Недетерминированной машиной Тьюринга (non-deterministic Turing machine) называется устройство, на каждом такте работы которого
- 66. Работу недетерминированной машины Тьюринга можно представить в виде серии догадок. В этом случае последовательность распознавания представляет
- 67. Размер (количество узлов) этого дерева экспоненциально зависит от размера входа. Однако, поскольку количество тактов в последовательности
- 68. Итак, временная сложность распознавания строки с помощью серии правильных догадок полиномиально зависит от размера исходных данных.
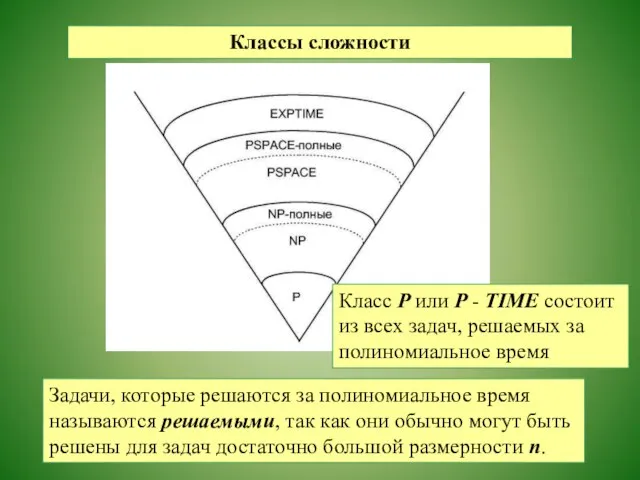
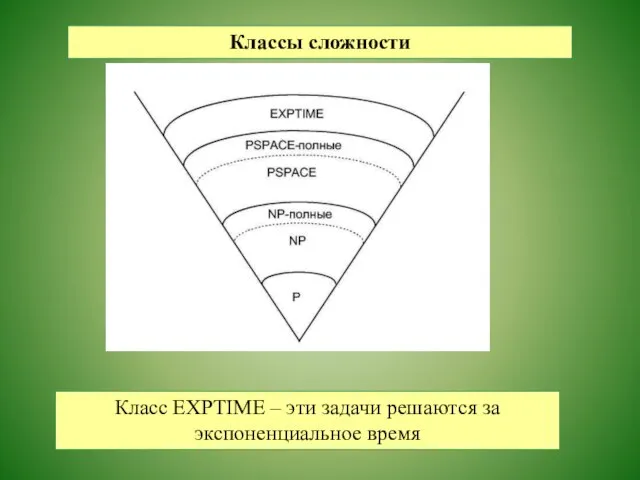
- 69. Классы сложности Задачи, которые решаются за полиномиальное время называются решаемыми, так как они обычно могут быть
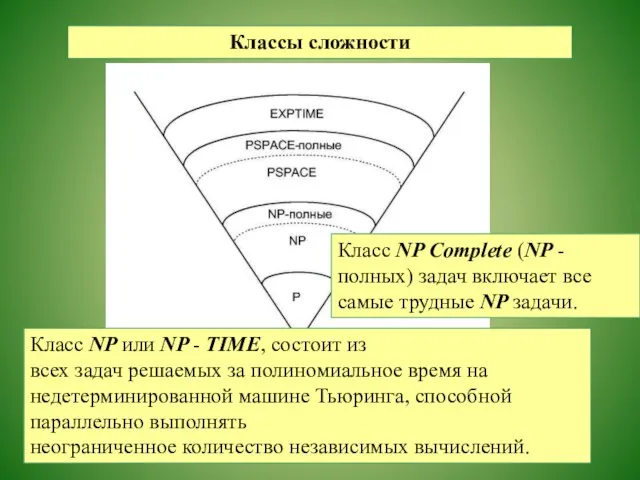
- 70. Классы сложности Класс NP или NP - TIME, состоит из всех задач решаемых за полиномиальное время
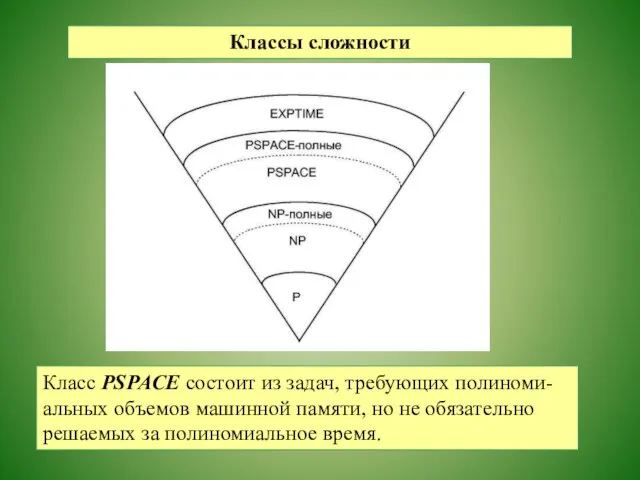
- 71. Классы сложности Класс PSPACE состоит из задач, требующих полиноми- альных объемов машинной памяти, но не обязательно
- 72. Классы сложности Класс EXPTIME – эти задачи решаются за экспоненциальное время
- 74. Скачать презентацию




![Алгоритм Евклида для вычисления наибольшего общего делителя begin g[0]: = b;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/544538/slide-5.jpg)

























































 Биостатистика. Сравнение выборок
Биостатистика. Сравнение выборок Презентация на тему: Длина
Презентация на тему: Длина Параллельный перенос
Параллельный перенос Нахождение дроби и процентов от числа
Нахождение дроби и процентов от числа Геометрические характеристики плоских сечений
Геометрические характеристики плоских сечений Презентация по математике Отношения и пропорции
Презентация по математике Отношения и пропорции  Статистический анализ данных
Статистический анализ данных Аттестационная работа. Создание творческого проекта «Задачи на движение»
Аттестационная работа. Создание творческого проекта «Задачи на движение» Окружность вписанная и описанная
Окружность вписанная и описанная Презентация по математике "Прямая и обратная пропорциональные зависимости" - скачать бесплатно
Презентация по математике "Прямая и обратная пропорциональные зависимости" - скачать бесплатно Многоугольники. Пентамино
Многоугольники. Пентамино Подготовка к ОГЭ. Методы, способствующие решению геометрических задач
Подготовка к ОГЭ. Методы, способствующие решению геометрических задач Уравнение окружности и прямой
Уравнение окружности и прямой Графики линейной функции, содержащей модуль
Графики линейной функции, содержащей модуль Треугольник и его виды
Треугольник и его виды Подготовка к ВПР (№1). Математика 6 класс
Подготовка к ВПР (№1). Математика 6 класс Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Презентация на тему Математический диктант 1 класс
Презентация на тему Математический диктант 1 класс  «Золотое сечение» (виртуальный факультатив)
«Золотое сечение» (виртуальный факультатив) Стереометрия 2 часть. Подготовка к ЕГЭ по математике 2019
Стереометрия 2 часть. Подготовка к ЕГЭ по математике 2019 Буквенная запись свойств сложения и вычитания
Буквенная запись свойств сложения и вычитания Вычислительные навыки на уроках математики
Вычислительные навыки на уроках математики Из истории возникновения теории вероятностей
Из истории возникновения теории вероятностей Лабиринты Выполнили: Трунцова Кристина и Морозова Мария Руководитель проекта: Кондрашова Елена Анатольевна
Лабиринты Выполнили: Трунцова Кристина и Морозова Мария Руководитель проекта: Кондрашова Елена Анатольевна  Наибольший общий делитель. Нахождение НОД. учитель математики Фролова Мария Викторовна МКОУ СОШ № 26 с. Мельничное Красноарм
Наибольший общий делитель. Нахождение НОД. учитель математики Фролова Мария Викторовна МКОУ СОШ № 26 с. Мельничное Красноарм Применение интегралов в решении задач
Применение интегралов в решении задач Расстояние между точками
Расстояние между точками Определение арифметической прогрессии
Определение арифметической прогрессии