Содержание
- 2. Постановка задачи Простейшая задача: в дискретные моменты времени наблюдаются значения функции ; требуется восстановить её значения
- 3. 2. Для функции известно её аналитическое представление, но вычисление каждого значения сопряжено с большим объёмом вычислений.
- 4. 3. Функция задаётся своими значениями в узлах , из интервала . В вычислительном процессе используется эта
- 5. 4. Задача численного решения определённого интеграла или дифференциального уравнения. 26.09.2014
- 6. Области использования аппроксимации : моделирование; планирование и статистическая обработка данных; определение значений функции при аргументах отсутствующих
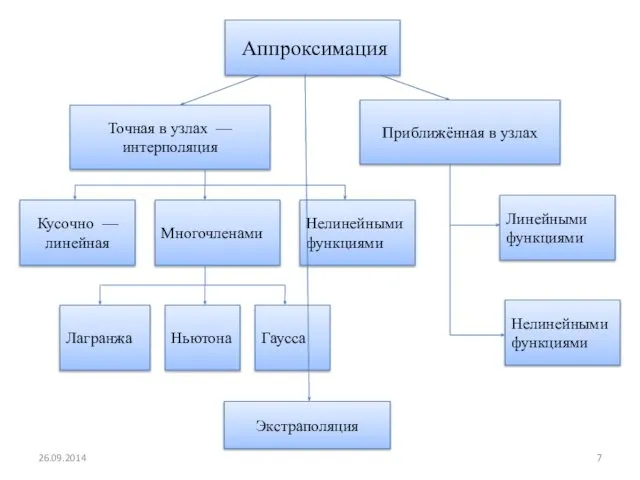
- 7. Аппроксимация Точная в узлах — интерполяция Приближённая в узлах Кусочно — линейная Многочленами Нелинейными функциями Гаусса
- 8. Аппроксимация 26.09.2014
- 9. Если аппроксимация функции происходит в промежуточных узлах, т.е. , причём тогда говорят о точной интерполяции. Интер
- 10. Интерполирование 26.09.2014
- 11. Если аппроксимация функции происходит вне рассматриваемого отрезка , тогда говорят об экстраполяции. экстра – вне. 26.09.2014
- 12. ИНТЕРПОЛИРОВАНИЕ Основные понятия. Задано множество точек , принадлежащих отрезку и значения функции в этих точках. Требуется
- 13. ОБОБЩЁННЫЙ ПОЛИНОМ – числовые коэффициенты, – множество функций, определённых на рассматриваемом отрезке и линейно независимых на
- 14. 1. Последовательность степеней . 2. Последовательность тригонометрических функций . 3. Последовательность экспонент . 4. Последовательность дробно-рациональных
- 15. Многочлен Тейлора m-ой степени: Для можно использовать известные разложения функций. 26.09.2014
- 16. Погрешность метода — остаточный член формулы Тейлора в форме Лагранжа: где c лежит между x и
- 17. Существование и единственность интерполяционного многочлена 26.09.2014 Теорема. Для таблично заданной функции на множестве узлов существует единственный
- 18. Будем искать многочлен Нужно найти коэффициенты a0, a1, ..., an. Они должны удовлетворять СЛУ В системе
- 19. Если система крамеровская, то решение СУЩЕСТВУЕТ и ЕДИНСТВЕННОЕ. Пусть m+1 = n+1, т.е. m = n.
- 20. Метод нахождения коэффициентов, используемый при доказательстве теоремы, называется методом неопределённых коэффициентов. 26.09.2014
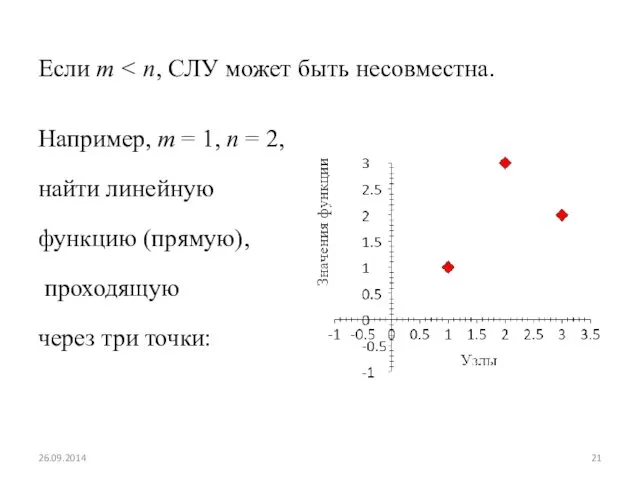
- 21. Если m Например, m = 1, n = 2, найти линейную функцию (прямую), проходящую через три
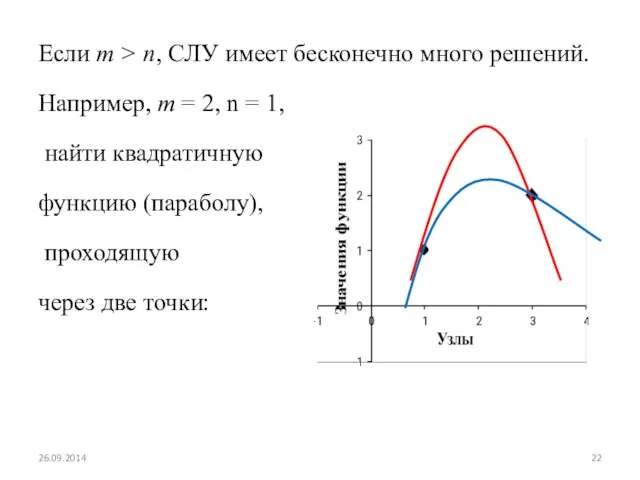
- 22. Если m > n, СЛУ имеет бесконечно много решений. Например, m = 2, n = 1,
- 23. Интерполяционный многочлен Лагранжа Выразим многочлен Ln(x) как линейную комбинацию значений f0, f1, ..., fn: 26.09.2014
- 24. Рассмотрим в качестве подсказки частные случаи. 1) n = 1: x0, x1 — узлы, f0, f1
- 25. 2) n=2: x0, x1, x2 — узлы, f0, f1 , f2— значения в узлах Найти при
- 26. Опр. Интерполяционным многочленом Лагранжа называется полином . Опр. Лагранжевы коэффициенты — Замечание: Лагранжевы коэффициенты удовлетворяют тождеству
- 27. Пример 1. Построить интерполяционный полином Лагранжа для функции, заданной таблицей Так как задано 4 узла интерполяции,
- 28. 26.09.2014 Можно вычислить приближённое значение в точке .
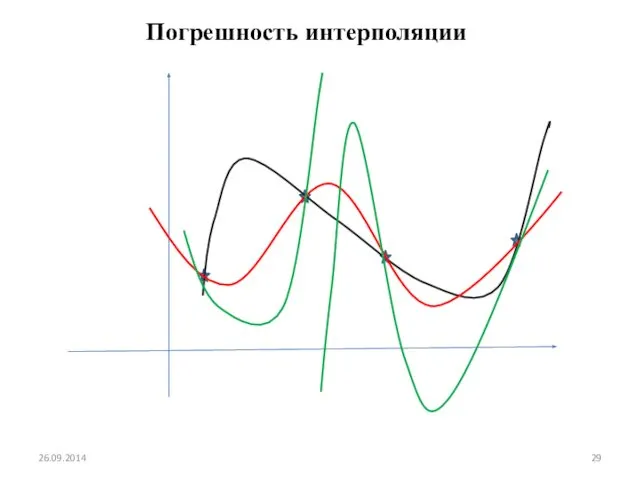
- 29. 26.09.2014 Погрешность интерполяции
- 30. Погрешность интерполяционного многочлена Лагранжа Предполагаем, что . Ln(x) — многочлен Лагранжа: для всех i=0,...,n [a,b] —
- 31. Запишем равенство где – многочлен определённый через узлы x0, x1, ..., xn С – некоторая постоянная
- 32. Введём в рассмотрение функцию 26.09.2014
- 33. Итак, существует : . Тогда и , т. к. получаем Отсюда 26.09.2014
- 34. Для остаточного члена получаем выражение 26.09.2014
- 35. Точное представление f (x) через её интерполяционный многочлен Лагранжа : где и зависит от x. Можно
- 37. Скачать презентацию




















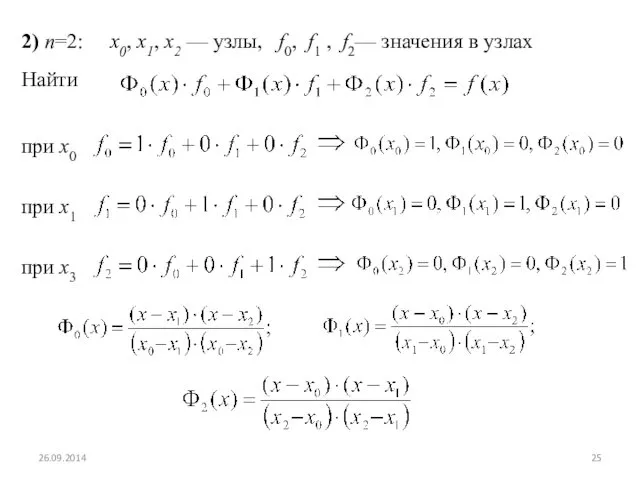









 Центральные и вписанные углы. Подготовка к ОГЭ
Центральные и вписанные углы. Подготовка к ОГЭ Решение математических задач прикладной направленности
Решение математических задач прикладной направленности Применение интеграла к решению физических задач
Применение интеграла к решению физических задач Деление десятичной дроби на натуральное число. 5 класс
Деление десятичной дроби на натуральное число. 5 класс Методические рекомендации по изложению темы «Площади плоских фигур» по геометрии в 7 - 9 классах
Методические рекомендации по изложению темы «Площади плоских фигур» по геометрии в 7 - 9 классах Математическая сказка на новый лад
Математическая сказка на новый лад Определение и основные свойства множеств
Определение и основные свойства множеств Урок алгебры в 7 классе По теме: «Степень числа»
Урок алгебры в 7 классе По теме: «Степень числа» Презентация по математике "Математика – гимнастика ума" - скачать бесплатно
Презентация по математике "Математика – гимнастика ума" - скачать бесплатно Противоположные числа Какие числа называют противоположными? Как на координатной прямой располагаются точки, соответствующие п
Противоположные числа Какие числа называют противоположными? Как на координатной прямой располагаются точки, соответствующие п Площадь криволинейной трапеции
Площадь криволинейной трапеции Понятие алгоритма. Свойства алгоритмов. Формы записей алгоритмов. Общие принципы построения алгоритмов
Понятие алгоритма. Свойства алгоритмов. Формы записей алгоритмов. Общие принципы построения алгоритмов Свойства умножения
Свойства умножения Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Исследовательская работа Арифметика Л.Ф. Магницкого – «врата учёности» М.В. Ломоносова Работу выполнила: ученица 10«Б» класса
Исследовательская работа Арифметика Л.Ф. Магницкого – «врата учёности» М.В. Ломоносова Работу выполнила: ученица 10«Б» класса  Спираль Архимеда
Спираль Архимеда Модуль числа. Противоположные числа
Модуль числа. Противоположные числа Замена переменной в двойном интеграле
Замена переменной в двойном интеграле Степень числа. Квадрат и куб числа. Математика, 5 класс
Степень числа. Квадрат и куб числа. Математика, 5 класс Презентация по математике "Решение задач по комбинаторике" - скачать
Презентация по математике "Решение задач по комбинаторике" - скачать  Решение уравнений
Решение уравнений Сложение смешанных дробей
Сложение смешанных дробей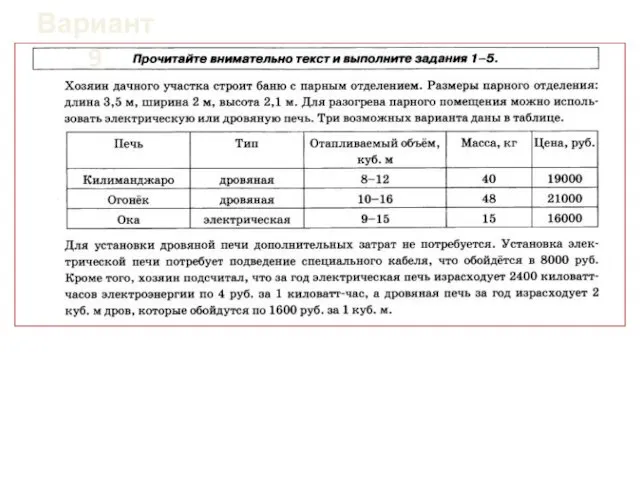 Варианты решения задач по строительству бани с парным отделением
Варианты решения задач по строительству бани с парным отделением Квадратичная функция, её график и свойства
Квадратичная функция, её график и свойства Построение графиков функций с помощью производных
Построение графиков функций с помощью производных Аттестационная работа. Методическая разработка по теме: «Теория графов»
Аттестационная работа. Методическая разработка по теме: «Теория графов» Повторение курса математики начальной школы
Повторение курса математики начальной школы Делители и кратные
Делители и кратные