Содержание
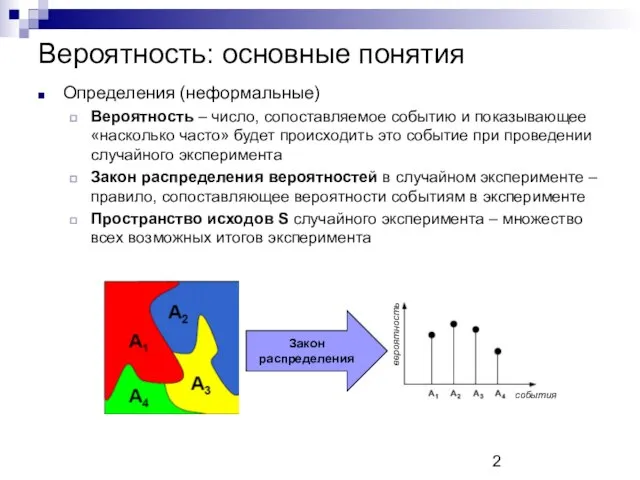
- 2. Вероятность: основные понятия Определения (неформальные) Вероятность – число, сопоставляемое событию и показывающее «насколько часто» будет происходить
- 3. Вероятность: свойства Свойство 1: Свойство 2: Свойство 3: Свойство 4: Для если ,то Свойство 5: Свойство
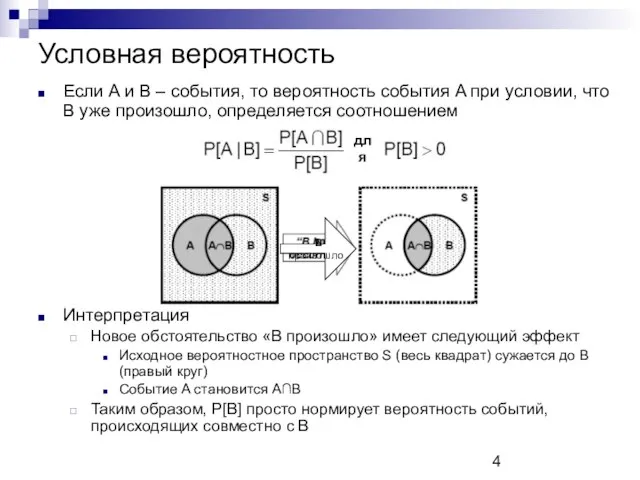
- 4. Условная вероятность Если A и B – события, то вероятность события A при условии, что B
- 5. Формула полной вероятности Пусть B1, B2, …, BN, – взаимоисключающие события, которые в объединении дают пространство
- 6. Формула Байеса Пусть B1, B2, …, BN дают разбиение S. Предположим, что произошло A. Какова вероятность
- 7. Формула Байеса и статистическое распознавание образов Для решения задачи классификации формула Байеса может быть переписана следующим
- 8. Простой пример Диагностическая задача: необходимо решить, болен ли пациент, основываясь на несовершенном тесте заболевания Некоторые больные
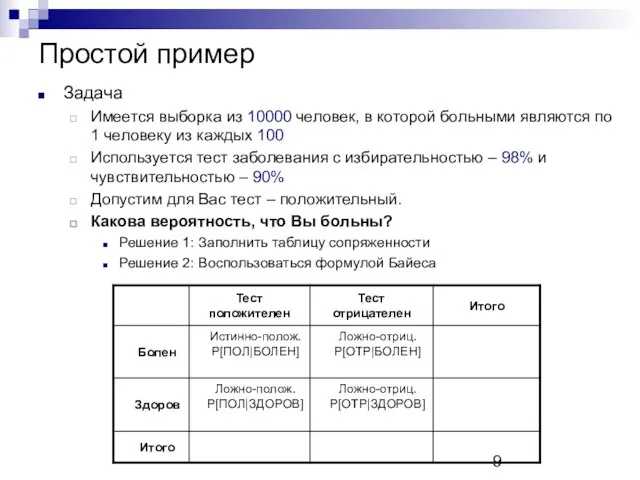
- 9. Простой пример Задача Имеется выборка из 10000 человек, в которой больными являются по 1 человеку из
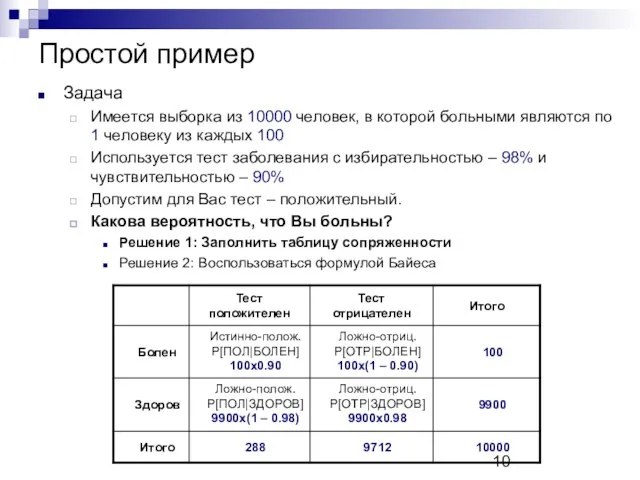
- 10. Простой пример Задача Имеется выборка из 10000 человек, в которой больными являются по 1 человеку из
- 11. Простой пример Задача Имеется выборка из 10000 человек, в которой больными являются по 1 человеку из
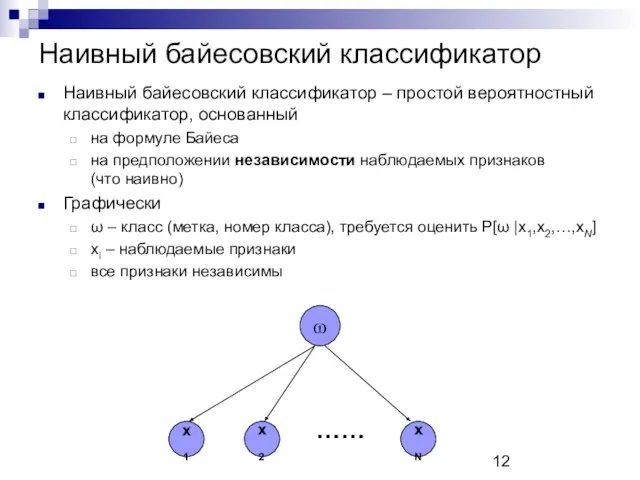
- 12. Наивный байесовский классификатор Наивный байесовский классификатор – простой вероятностный классификатор, основанный на формуле Байеса на предположении
- 13. Наивный байесовский классификатор Вероятностная модель наивного байесовского классификатора Строго говоря, Но в виду условной независимости признаков
- 14. Наивный байесовский классификатор Наивный байесовский классификатор – комбинация вероятностной модели и решающего правила «максимум апостериорной вероятности»
- 15. Наивный байесовский классификатор Задача. Отнести текстовые документы к одному из предопределенных классов (спорт, политика, экономика,…) Дано.
- 16. Наивный байесовский классификатор Задача. Отнести текстовые документы к одному из предопределенных классов (спорт, политика, экономика,…) Дано.
- 17. Наивный байесовский классификатор Задача. Отнести текстовые документы к одному из предопределенных классов (спорт, политика, экономика,…) Дано.
- 18. Наивный байесовский классификатор Задача. Отнести текстовые документы к одному из предопределенных классов (спорт, политика, экономика,…) Дано.
- 19. Критерий отношения правдоподобия Пусть объект классифицируется на основании измерения (вектора характеристик) x Разумное решающее правило: «Выбрать
- 20. Критерий отношения правдоподобия В случае 2-классовой задачи классификации: Если P(ω1 |x) > P(ω2 |x), выбрать ω1,
- 21. Критерий отношения правдоподобия: пример Используя критерий отношения правдоподобия, построить решающее правило для следующих условных плотностей классов
- 22. Критерий отношения правдоподобия: пример Предыдущий пример понятен с интуитивной точки зрения, т.к. правдоподобия идентичны и отличаются
- 23. Вероятность ошибки Мерой качества любого решающего правила может выступать с вероятность ошибки P[error] В соответствии с
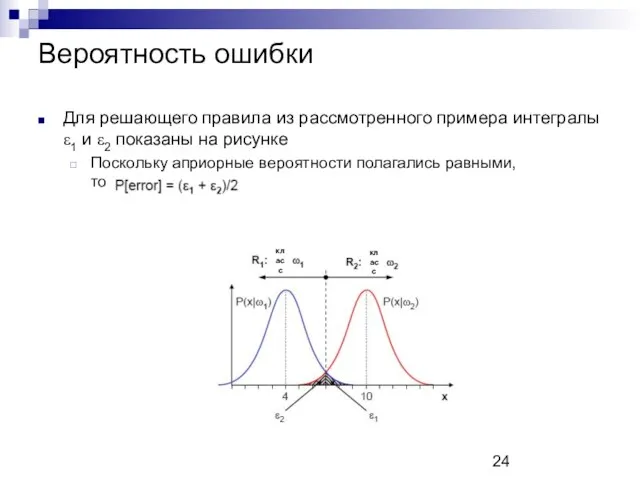
- 24. Вероятность ошибки Для решающего правила из рассмотренного примера интегралы ε1 и ε2 показаны на рисунке Поскольку
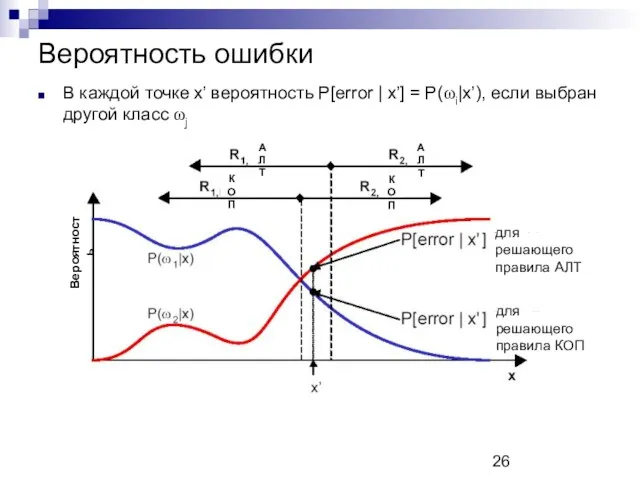
- 25. Вероятность ошибки Выясним, насколько хорош критерий отношения правдоподобия в смысле вероятности ошибки Для этого удобно выразить
- 26. Вероятность ошибки АЛТ Вероятность для решающего правила АЛТ АЛТ КОП КОП для решающего правила КОП В
- 27. Вероятность ошибки Для любой задачи минимальная вероятность ошибки достигается, если в качестве решающего правила используется критерий
- 28. Байесовский риск До сих пор полагалось, что цена ошибочного отнесения к классу ω1 образца, принадлежащего классу
- 29. Байесовский риск Какое решающее правило минимизирует байесовский риск? Заметим, что Байесовский риск выражается как Для любого
- 30. Байесовский риск Подставим последнее уравнение в выражение байесовского риска Избавимся от интегралов по R2 Т.к. первые
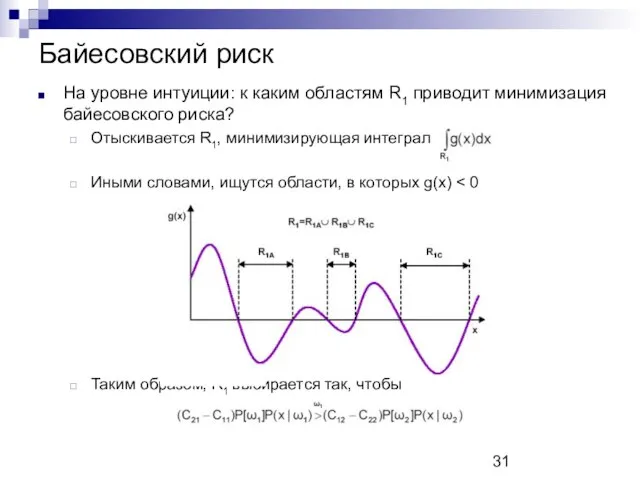
- 31. Байесовский риск На уровне интуиции: к каким областям R1 приводит минимизация байесовского риска? Отыскивается R1, минимизирующая
- 32. Байесовский риск На уровне интуиции: к каким областям R1 приводит минимизация байесовского риска? Отыскивается R1, минимизирующая
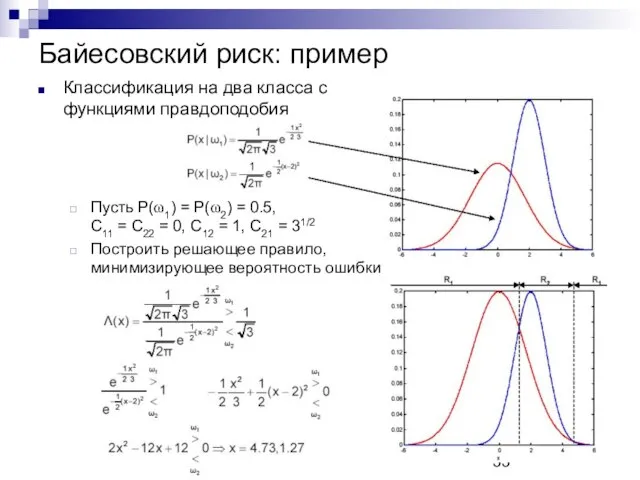
- 33. Байесовский риск: пример Классификация на два класса с функциями правдоподобия Пусть P(ω1) = P(ω2) = 0.5,
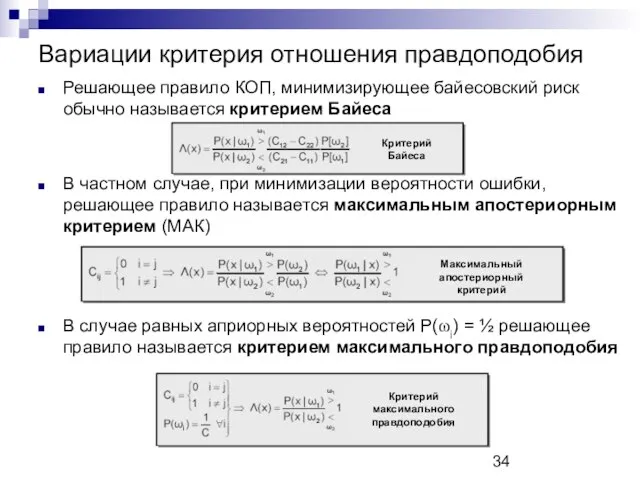
- 34. Вариации критерия отношения правдоподобия Решающее правило КОП, минимизирующее байесовский риск обычно называется критерием Байеса В частном
- 35. Правило минимизации P[error] для многоклассовых задач Правило минимизации вероятности ошибки P[error] легко обобщается на случай многих
- 36. Правило минимизации P[error] для многоклассовых задач Правило минимизации вероятности ошибки P[error] легко обобщается на случай многих
- 37. Минимизация байесовского риска для многоклассовых задач Новые обозначения αi – решение о выборе класса ωi α(x)
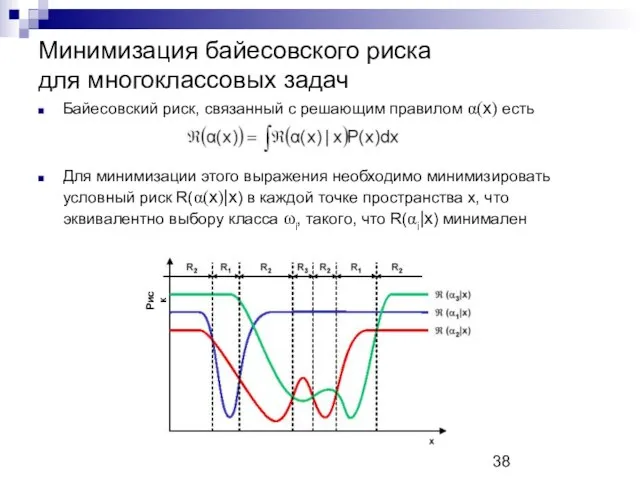
- 38. Минимизация байесовского риска для многоклассовых задач Байесовский риск, связанный с решающим правилом α(x) есть Для минимизации
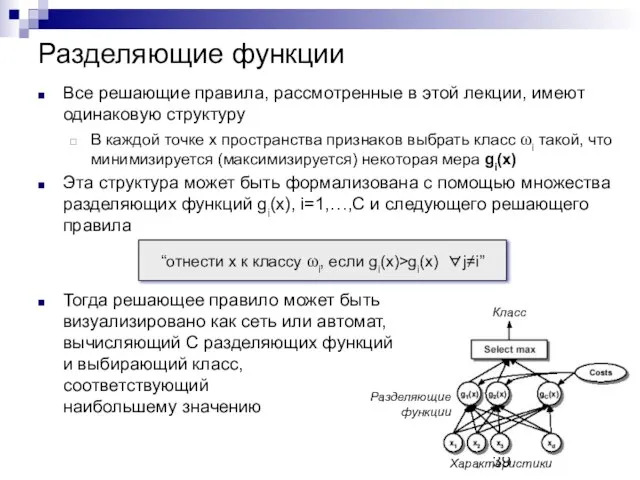
- 39. Разделяющие функции Все решающие правила, рассмотренные в этой лекции, имеют одинаковую структуру В каждой точке x
- 40. Разделяющие функции Основные критерии как разделяющие функции
- 41. Байесовские классификаторы для нормально распределенных классов Для случая нормально распределенных классов критерий минимизации ошибки (максимизации апостериорной
- 42. Байесовские классификаторы для нормально распределенных классов Выражения для гауссовых плотностей в общем виде Плотность многомерного нормального
- 43. Случай 1: Σi = σ2I Случай возникает. когда характеристики образцов статистически независимы и имеют одинаковую вариацию
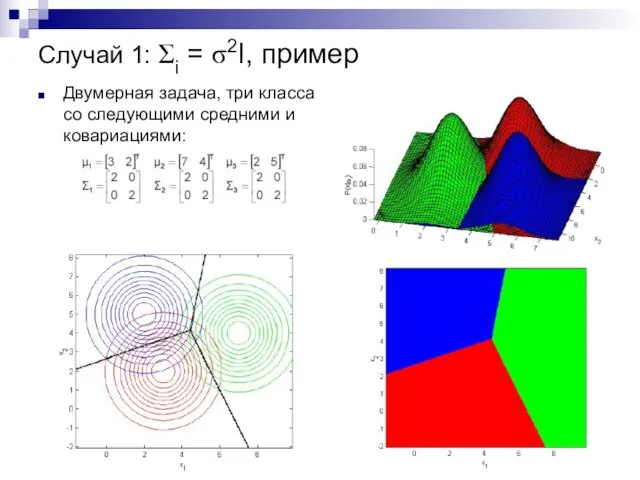
- 44. Случай 1: Σi = σ2I, пример Двумерная задача, три класса со следующими средними и ковариациями:
- 45. Случай 2: Σi = Σ (Σ – диагональная) Классы по-прежнему имеют одинаковую матрицу ковариации, но характеристики
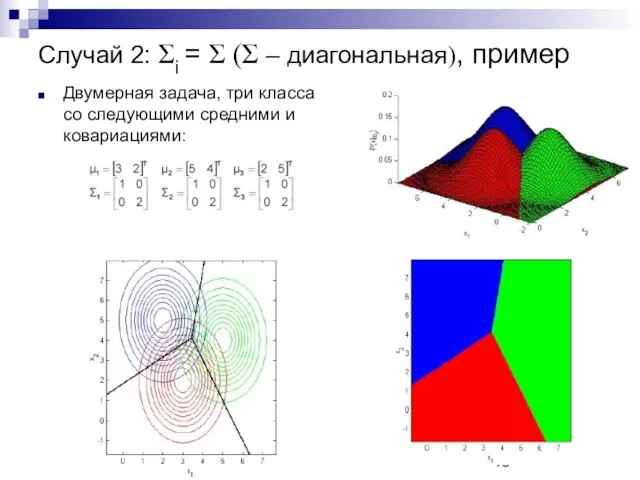
- 46. Случай 2: Σi = Σ (Σ – диагональная), пример Двумерная задача, три класса со следующими средними
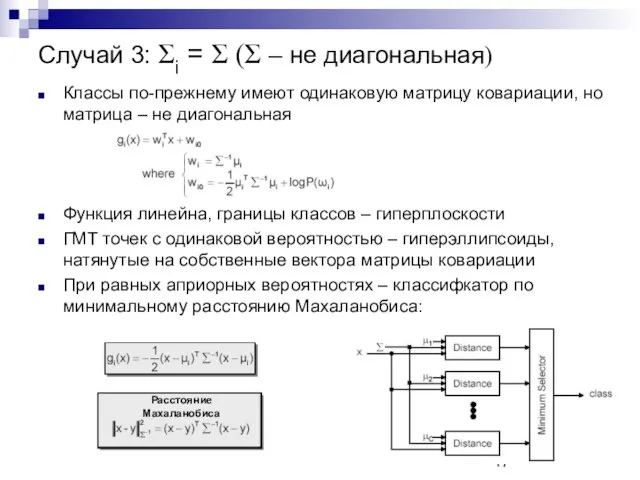
- 47. Случай 3: Σi = Σ (Σ – не диагональная) Классы по-прежнему имеют одинаковую матрицу ковариации, но
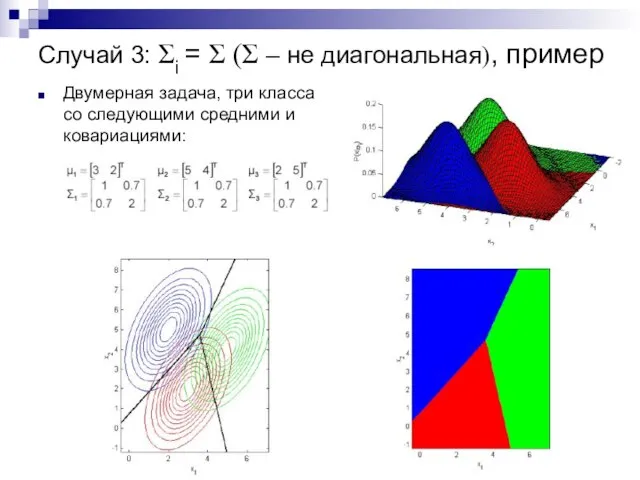
- 48. Случай 3: Σi = Σ (Σ – не диагональная), пример Двумерная задача, три класса со следующими
- 49. Случай 4: Σi = σi2I Классы имеют разные матрицы ковариации, которые пропорциональны единичной матрице Границы классов
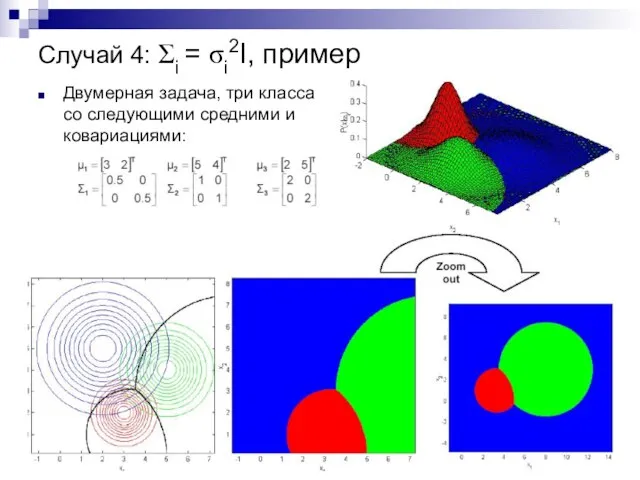
- 50. Случай 4: Σi = σi2I, пример Двумерная задача, три класса со следующими средними и ковариациями:
- 51. Случай 5: Σi ≠ Σj (общий случай) Для общего случая разделяющая функция выглядит так: Или, после
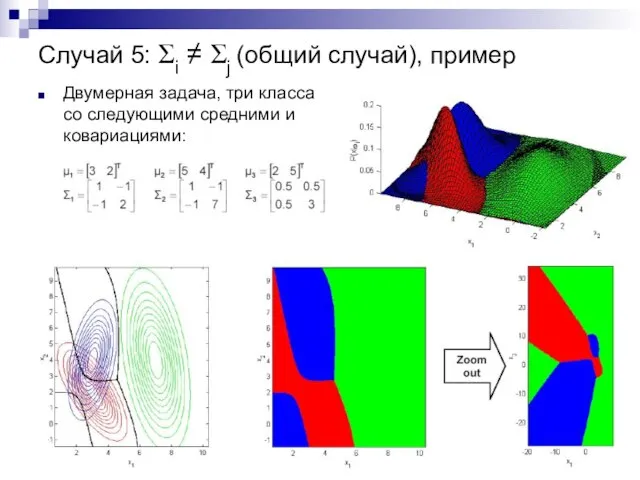
- 52. Случай 5: Σi ≠ Σj (общий случай), пример Двумерная задача, три класса со следующими средними и
- 53. Построить линейную разделяющую функцию для трехмерной двухклассовой задачи распознавания по следующим данным: Решение Классифицировать тестовый образец
- 55. Скачать презентацию























![Правило минимизации P[error] для многоклассовых задач Правило минимизации вероятности ошибки P[error]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/507270/slide-34.jpg)
![Правило минимизации P[error] для многоклассовых задач Правило минимизации вероятности ошибки P[error]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/507270/slide-35.jpg)









 Элементы комбинаторики, статистики и теории вероятностей. Решение заданий В 10 ЕГЭ
Элементы комбинаторики, статистики и теории вероятностей. Решение заданий В 10 ЕГЭ Задачи логического характера
Задачи логического характера Тригонометрические неравенства
Тригонометрические неравенства Microsoft Excel. Анализ данных
Microsoft Excel. Анализ данных задачи по математике (6 класс)
задачи по математике (6 класс) Построение сечений методом следа секущей плоскости
Построение сечений методом следа секущей плоскости Презентация по математике "Число пи" - скачать бесплатно
Презентация по математике "Число пи" - скачать бесплатно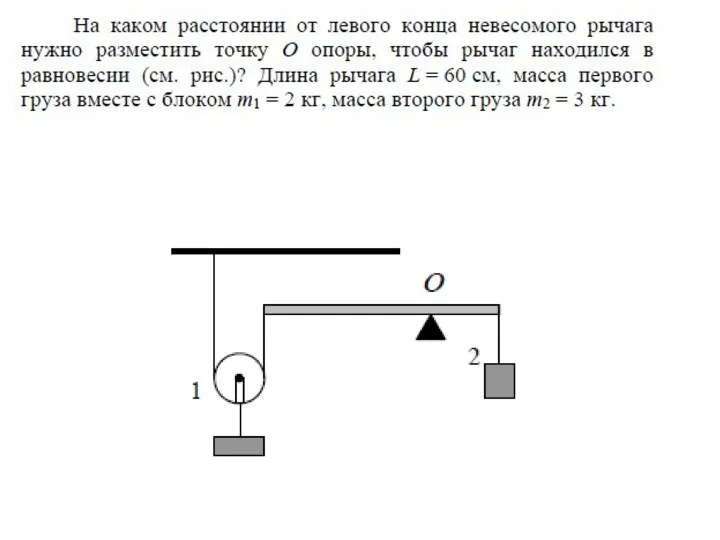 Задачи на расстояние
Задачи на расстояние Аттестационная работа. Доли. Обыкновенные дроби. (5 класс)
Аттестационная работа. Доли. Обыкновенные дроби. (5 класс) Алгебра высказываний. Высказывания и операции над ними
Алгебра высказываний. Высказывания и операции над ними Объем пирамиды
Объем пирамиды Мини-проекты по математике Формирование математической грамотности через составление задач
Мини-проекты по математике Формирование математической грамотности через составление задач Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения Задачи с практическим содержанием по теме: «Арифметическая и геометрическая прогрессии»
Задачи с практическим содержанием по теме: «Арифметическая и геометрическая прогрессии»  Логика. Эквиваленция
Логика. Эквиваленция Проект по математике на тему Симметрия в архитектуре, природе, технике и искусстве
Проект по математике на тему Симметрия в архитектуре, природе, технике и искусстве Корреляция. Показатель корреляции
Корреляция. Показатель корреляции Сумма углов треугольника
Сумма углов треугольника Причинно-следственная диаграмма Исикавы
Причинно-следственная диаграмма Исикавы Понятие вектора. Равенство вектора
Понятие вектора. Равенство вектора Метод интервалов. Решаем неравенства!
Метод интервалов. Решаем неравенства! Современный урок. Математика
Современный урок. Математика Формулы сокращенного умножения. (Найди ошибку) 7 класс
Формулы сокращенного умножения. (Найди ошибку) 7 класс Предел и непрерывность функции
Предел и непрерывность функции Правила сложения и вычитания десятичной дроби
Правила сложения и вычитания десятичной дроби Машины примеры Математический тренажёр
Машины примеры Математический тренажёр  Тақ көрсеткішті функция қасиеттері
Тақ көрсеткішті функция қасиеттері Измерение отрезков
Измерение отрезков