Представление биномиальных куч
Поскольку количество детей у узлов варьируется в широких пределах,
ссылка на детей осуществляется через левого ребенка, а остальные дети образуют односвязный список. Каждый узел в биномиальной куче представляется набором полей:
key — ключ (вес) элемента,
parent — указатель на родителя узла,
child — указатель на левого ребенка узла,
sibling — указатель на правого брата узла,
degree — степень узла (количество дочерних узлов данного узла).
Корни деревьев, из которых состоит куча, содержатся в так называемом списке корней, при проходе по которому степени соответствующих корней находятся в возрастающем порядке. Доступ к куче осуществляется ссылкой на первый корень в списке корней.









 Одночлен и его стандартный вид
Одночлен и его стандартный вид Умножение многозначных чисел
Умножение многозначных чисел Аттестационная работа. Рисуем на координатной плоскости
Аттестационная работа. Рисуем на координатной плоскости Площадь прямоугольника. 8 класс
Площадь прямоугольника. 8 класс Расстояние от точки до фигуры
Расстояние от точки до фигуры Все ли в мире состоит из многогранников
Все ли в мире состоит из многогранников Элементарное введение в метод структурных схем
Элементарное введение в метод структурных схем Урок математики 4 класс «Письменный приём умножения многозначного числа на двузначное» Учитель начальных классов МОУ СОШ №11 г.П
Урок математики 4 класс «Письменный приём умножения многозначного числа на двузначное» Учитель начальных классов МОУ СОШ №11 г.П Биостатистика. Критерии согласия Колмогорова-Смирнова
Биостатистика. Критерии согласия Колмогорова-Смирнова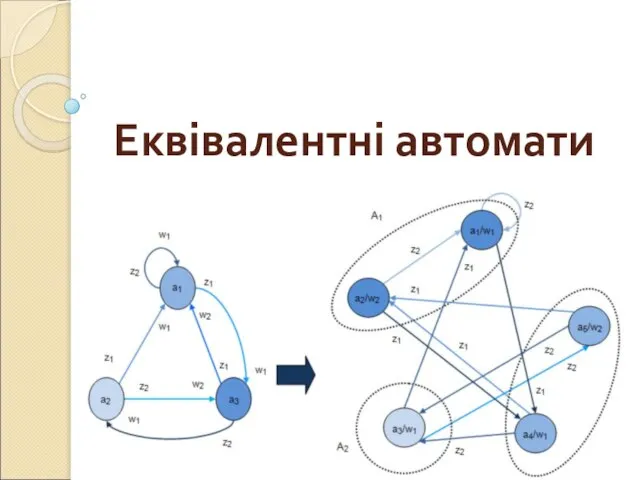 Еквівалентні автомати
Еквівалентні автомати Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Производная интеграла по переменному верхнему пределу
Производная интеграла по переменному верхнему пределу Виды углов. (Задачи, 5 класс)
Виды углов. (Задачи, 5 класс) Многоугольники. Параллелограмм. 8 класс
Многоугольники. Параллелограмм. 8 класс Презентация на тему Числовые и буквенные выражения
Презентация на тему Числовые и буквенные выражения  Вычисление дробей. Устная работа
Вычисление дробей. Устная работа Способы решения задачи на нахождение площади поверхности фигуры, составленной из прямоугольных параллелепипедов
Способы решения задачи на нахождение площади поверхности фигуры, составленной из прямоугольных параллелепипедов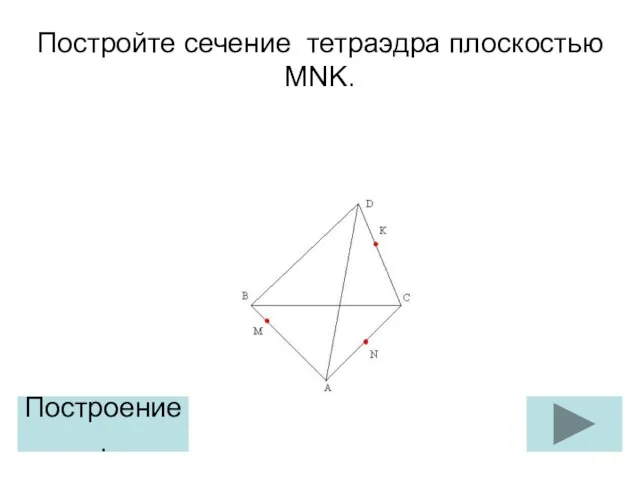 Тетраэдр. Построение сечения (задание 3)
Тетраэдр. Построение сечения (задание 3) Частные производные различных порядков. Производная сложной функции. (Семинар 23)
Частные производные различных порядков. Производная сложной функции. (Семинар 23) Противоположные числа
Противоположные числа Точки на прямой. Вопросы, упражнения
Точки на прямой. Вопросы, упражнения Производная интеграла по переменному верхнему пределу
Производная интеграла по переменному верхнему пределу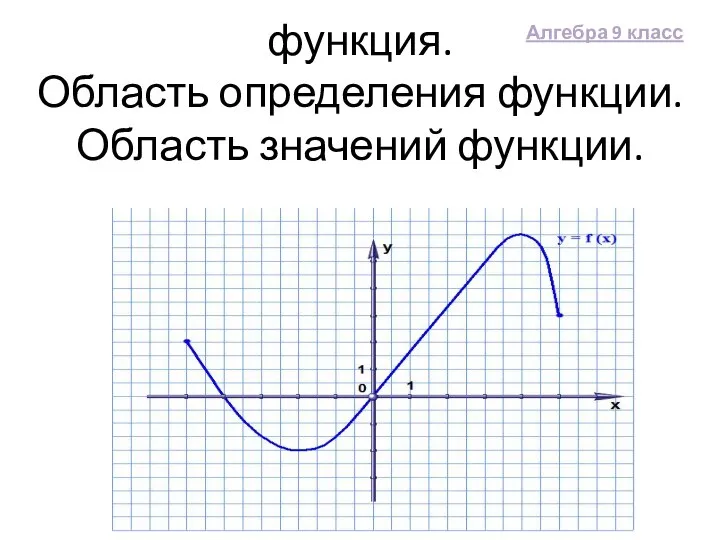 Функция. Область определения функции. Область значений функции. Алгебра 9 класс
Функция. Область определения функции. Область значений функции. Алгебра 9 класс Старинные единицы измерения
Старинные единицы измерения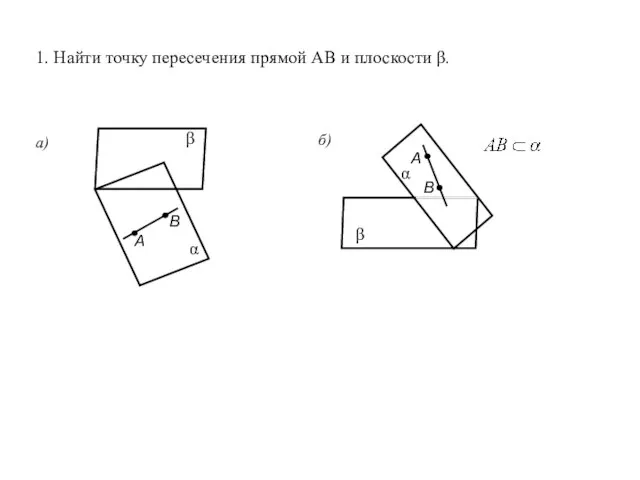 У-21_Построение_сечений[1] (2)
У-21_Построение_сечений[1] (2) Прямая пропорциональность
Прямая пропорциональность Построение диаграмм и графиков в электронных таблицах
Построение диаграмм и графиков в электронных таблицах Саннар. Чама саны приблизительные числительные
Саннар. Чама саны приблизительные числительные