Числа Фибоначчи

Происхождение последовательности:

Последовательность была известна в Древней Индии, но более широко известна

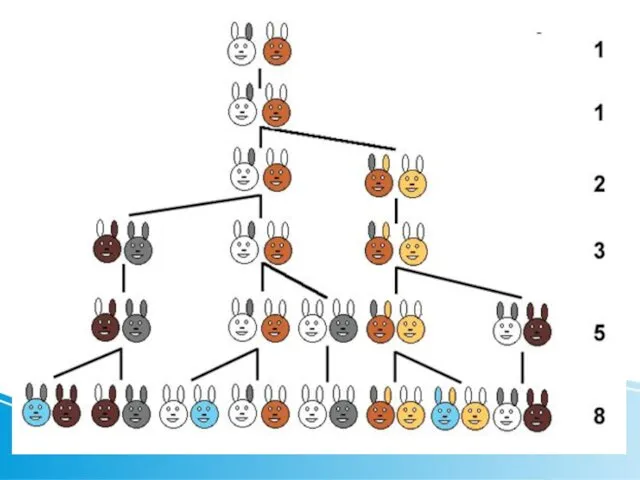
Условие:
Есть пара новорождённых крольчат (самка и самец), отличающихся интересной особенностью –

Задача про кроликов Решение

Решение:
Имеем:
Одну пару кроликов в начале первого месяца, которая

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,

Интересные свойства последовательности чисел Фибоначчи. Символическая запись

Свойства последовательности:

(Fn)2+(Fn+1)2+2(Fn*Fn+1)=____

1 2 3 4 5 6 7 8 9

МУЗЫКАЛЬНАЯ ПАУЗА

ЗАКЛЮЧЕНИЕ
Числа Фибоначчи – простейшая последовательность чисел, однако она имеет множество

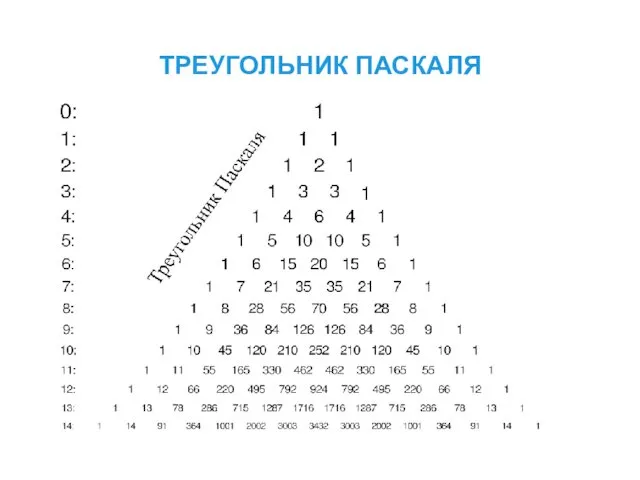
ТРЕУГОЛЬНИК ПАСКАЛЯ

19 июня 1623 г

- 19 августа 1662 г.

математик, физик, писатель

ТРЕУГОЛЬНИК ПАСКАЛЯ

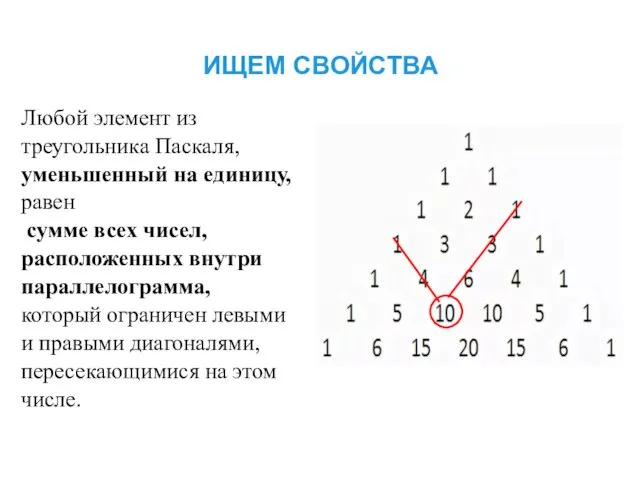
ИЩЕМ СВОЙСТВА

Любой элемент из треугольника Паскаля, уменьшенный на единицу, равен
сумме

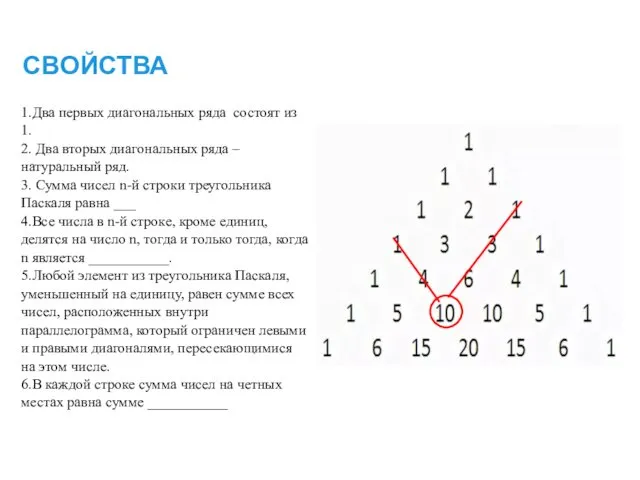
СВОЙСТВА

1.Два первых диагональных ряда состоят из 1.
2. Два вторых диагональных ряда

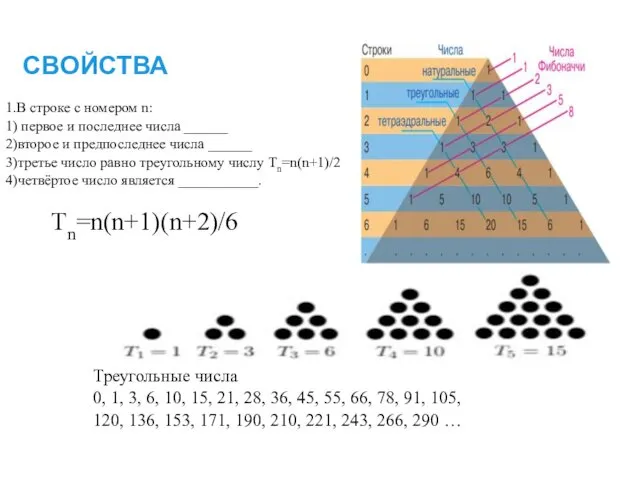
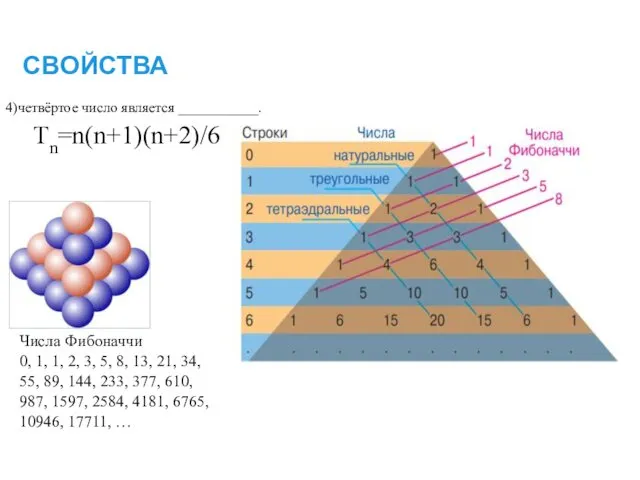
СВОЙСТВА

1.В строке с номером n:
1) первое и последнее числа ______
2)второе

СВОЙСТВА

Числа Фибоначчи
0, 1, 1, 2, 3, 5, 8, 13, 21, 34,

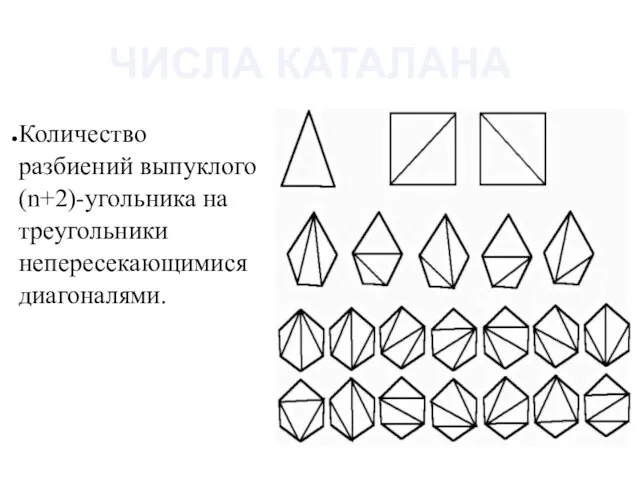
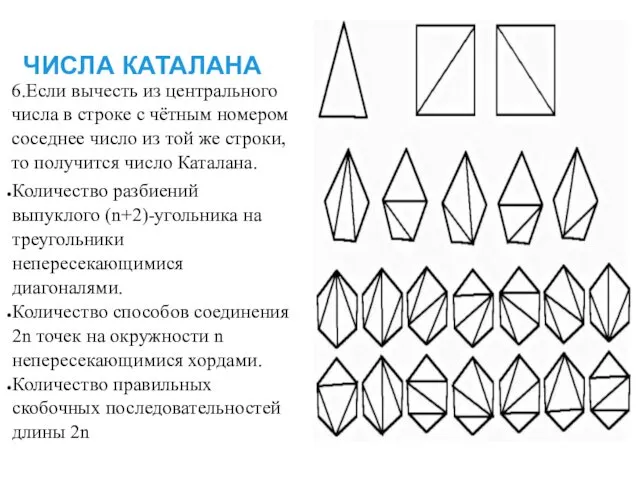
Количество
разбиений выпуклого (n+2)-угольника на треугольники непересекающимися диагоналями.

ЧИСЛА КАТАЛАНА

ЧИСЛА КАТАЛАНА

6.Если вычесть из центрального числа в строке с чётным номером

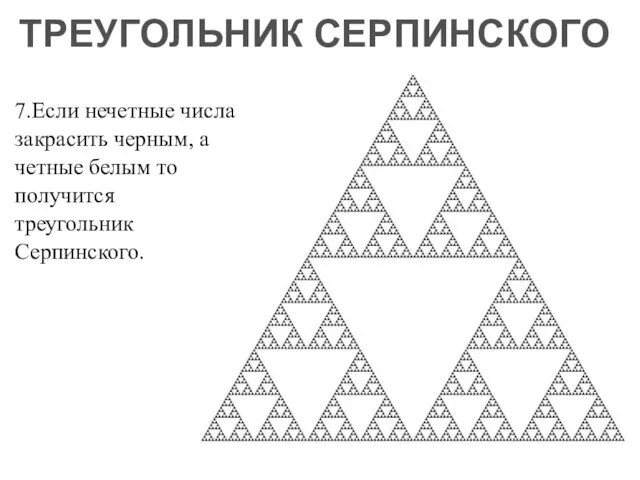
7.Если нечетные числа закрасить черным, а четные белым то получится треугольник

ЗАКЛЮЧЕНИЕ

Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок.