Содержание
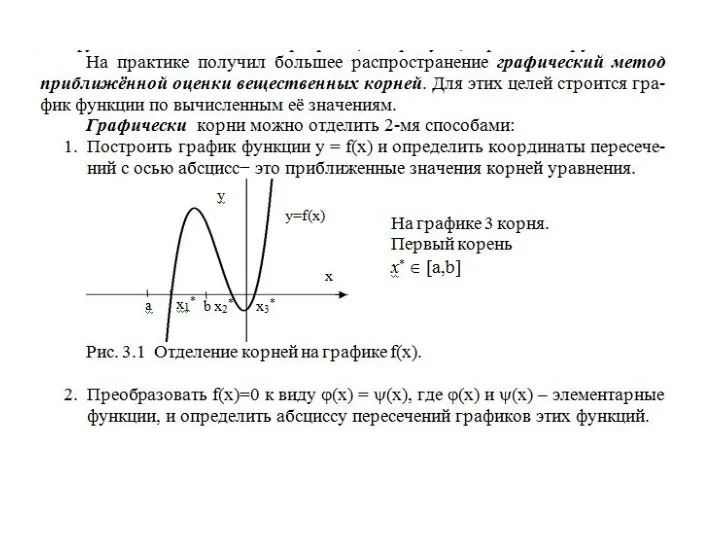
- 5. 3.1. Отделение корней нелинейного уравнения.
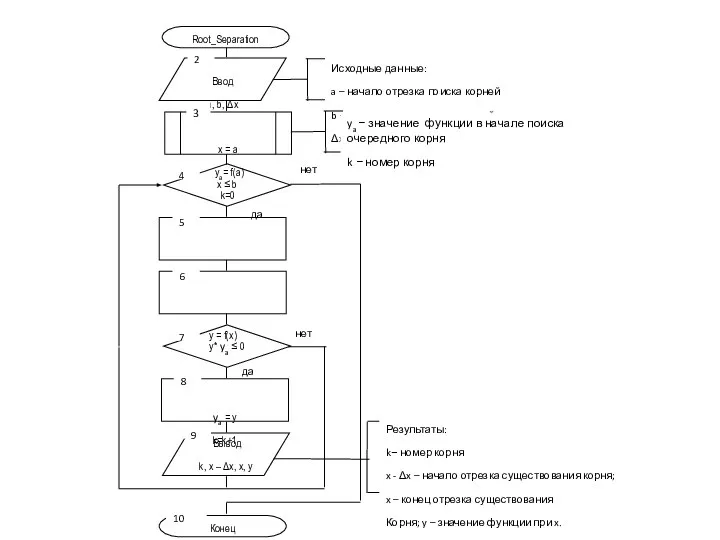
- 13. Рис. 3.3 Схема алгоритма отделения корней.
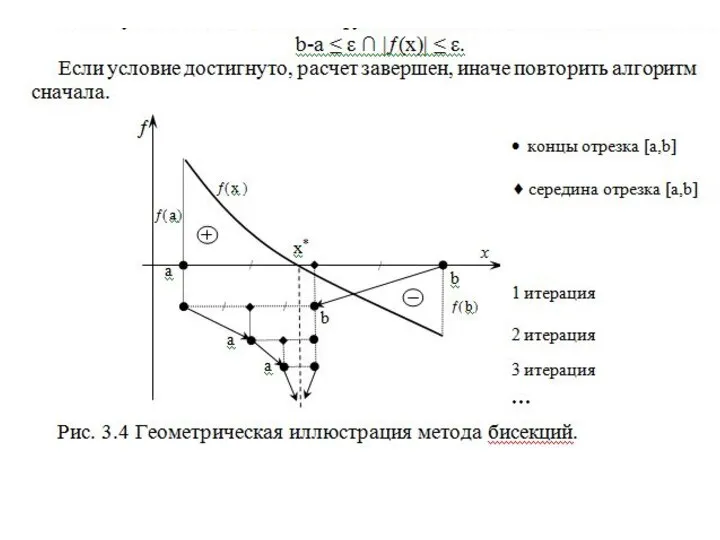
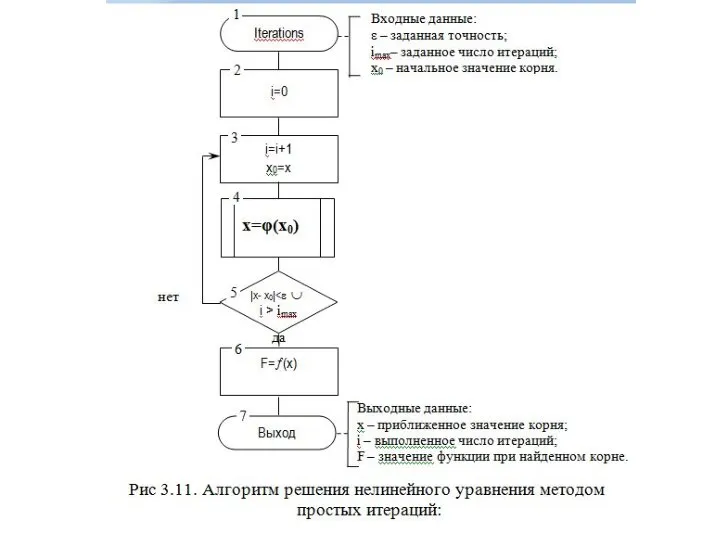
- 15. 3.2. Алгоритмы уточнения корней уравнения.
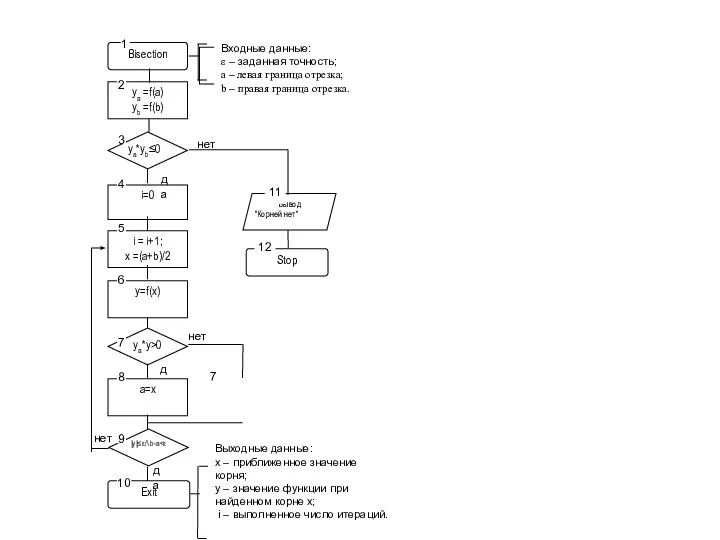
- 18. Рис. 3.5 Схема алгоритма метода бисекций (дихотомии)
- 19. Exit Вывод "Корней нет" да ya =f(a) yb =f(b) i = i+1; x =(a+b)/2 i=0 ya*yb≤0
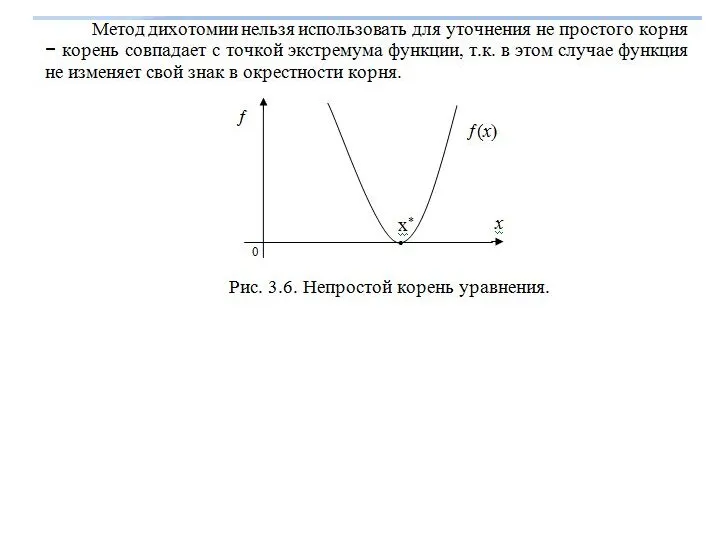
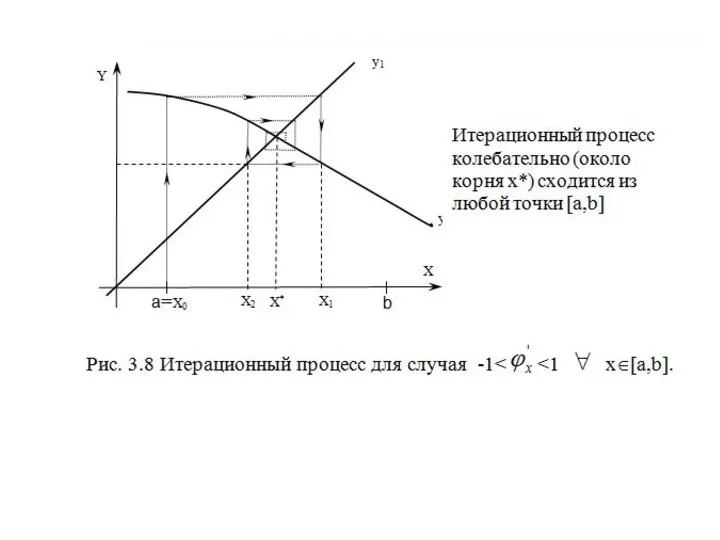
- 26. x∈[a,b]. x∈[a,b].
- 36. Проверим полученное значение, подставив в исходное уравнение: Значение f(x) близко к 0 с точностью, близкой к
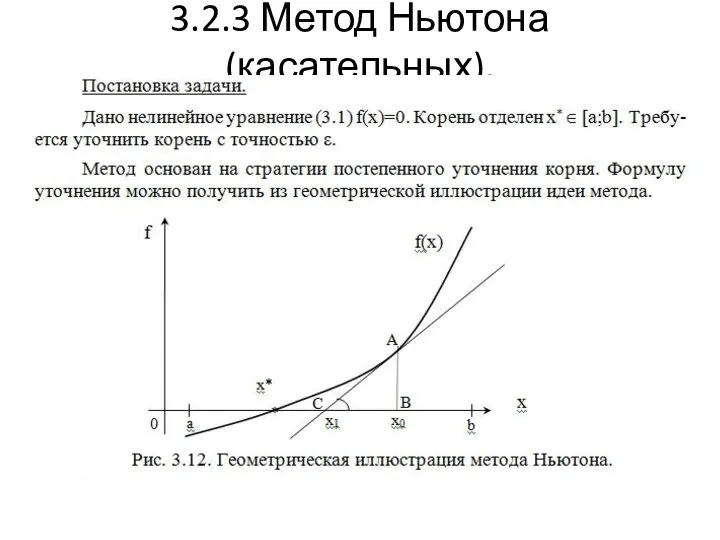
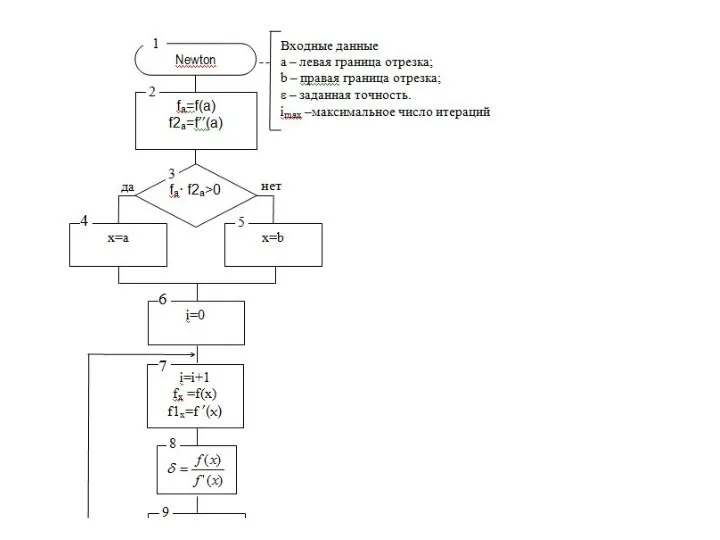
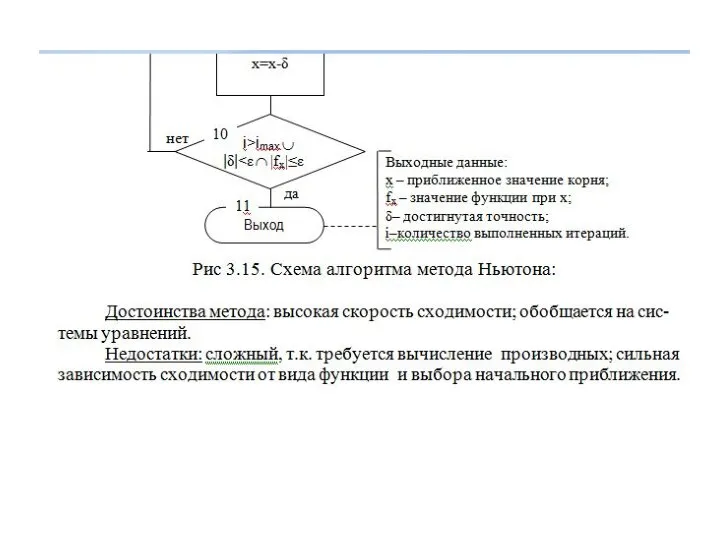
- 37. 3.2.3 Метод Ньютона (касательных).
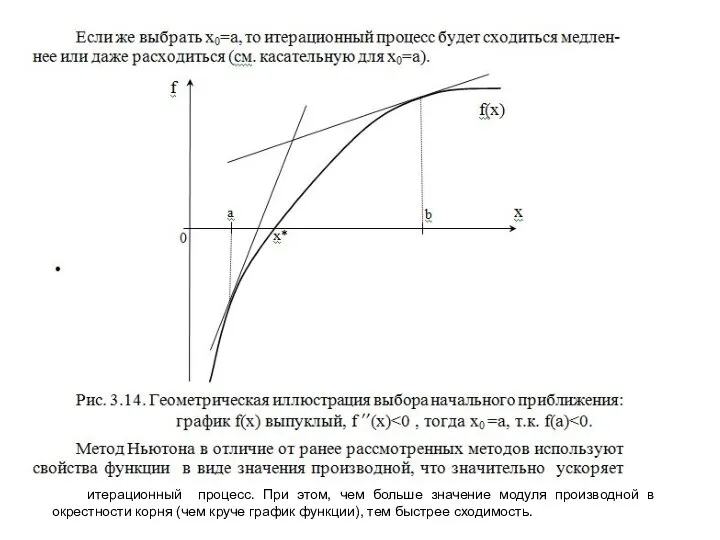
- 41. итерационный процесс. При этом, чем больше значение модуля производной в окрестности корня (чем круче график функции),
- 45. Скачать презентацию



















![x∈[a,b]. x∈[a,b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1466149/slide-25.jpg)








 Презентация на тему Деление на трехзначное число
Презентация на тему Деление на трехзначное число  Преобразование тригонометрических выражений (вывод тригонометрических формул)
Преобразование тригонометрических выражений (вывод тригонометрических формул) Вычисление интегралов
Вычисление интегралов Поиски неизвестного количества
Поиски неизвестного количества Множества. Операции над множествами
Множества. Операции над множествами Применение распределительного свойства умножения
Применение распределительного свойства умножения ЕГЭ. Производная в заданиях уровня В. 2 часть
ЕГЭ. Производная в заданиях уровня В. 2 часть Округление чисел
Округление чисел Алгебра, 7 класс. Автор презентации: учитель математики МОУ «Средняя общеобразовательная школа с углубленным изучением отд
Алгебра, 7 класс. Автор презентации: учитель математики МОУ «Средняя общеобразовательная школа с углубленным изучением отд Способы решения тригонометрических уравнений
Способы решения тригонометрических уравнений Площадь треугольника
Площадь треугольника Геометрия. Планиметрия
Геометрия. Планиметрия Решение логических задач табличным способом
Решение логических задач табличным способом ЕГЭ - 2015. Некоторые задачи, решения, ошибки учеников
ЕГЭ - 2015. Некоторые задачи, решения, ошибки учеников Выполнил ученик 11 класса Юдин Владимир Учитель математики
Выполнил ученик 11 класса Юдин Владимир Учитель математики  Показательная функция. Порядок роста и убывания функции
Показательная функция. Порядок роста и убывания функции Квадратные уравнения
Квадратные уравнения Свойства числовых неравенств
Свойства числовых неравенств Двуполостный гиперболоид
Двуполостный гиперболоид Линейчатые поверхности. (Лекция 6)
Линейчатые поверхности. (Лекция 6) Множества. Операции над множествами. Задачи
Множества. Операции над множествами. Задачи Признаки делимости на 10, на 5, на 2 Автор: Еремеева М.В. Бийск 2010
Признаки делимости на 10, на 5, на 2 Автор: Еремеева М.В. Бийск 2010 Элементы теории ошибок измерений. Лекция №6
Элементы теории ошибок измерений. Лекция №6 Виды симметрии в архитектуре
Виды симметрии в архитектуре Выборочное наблюдение
Выборочное наблюдение Методы решения систем уравнений второй степени. 9 класс
Методы решения систем уравнений второй степени. 9 класс Аксиомы, теоремы и формулы теории вероятностей
Аксиомы, теоремы и формулы теории вероятностей Решение задач с помощью систем уравнений второй степени
Решение задач с помощью систем уравнений второй степени