Содержание
- 2. Понятие иррационального числа Построение отрезка заданной длины Понятие положительного действительного числа Действия над действительными числами Геометрическая
- 3. При измерении длины отрезка а при единичном отрезке е могут возникнуть следующие ситуации: 1. Единичный отрезок
- 5. 3. Единичный отрезок е и любая его часть не укладывается в отрезке а целое число раз,
- 6. Рассмотрим процесс измерения длины отрезка nе n и n+1 есть приближенные значения длины отрезка а при
- 7. Будем укладывать е1 в отрезке а1
- 10. Бесконечные десятичные периодические дроби являются рациональными числами (они могут быть представлены в виде обыкновенных дробей)
- 11. В VI в. до н.э. в школе Пифагора, где была поставлена и решена задача: существует ли
- 12. Доказательство («от противного») m – четно, т. е. m = 2k, k ∈ N ⇒ 4k2
- 13. Доказательство аналогично Иррациональным числом называется бесконечная десятичная непериодическая дробь n,n1n2 … nк… Множество положительных иррациональных чисел
- 14. К понятию иррационального числа можно прийти не только через процесс десятичного измерения длин отрезков, но при
- 15. 12 1,42 1,412 1,4142 и т. д.
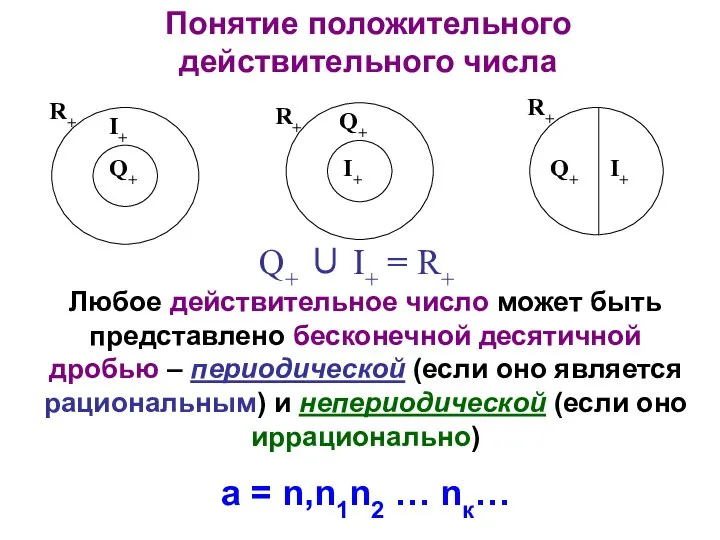
- 16. Понятие положительного действительного числа Q+ ∪ I+ = R+ Любое действительное число может быть представлено бесконечной
- 17. х = n,n1n2 … nк… у = m,m1m2 … mк… ОТНОШЕНИЕ ПОРЯДКА НА МНОЖЕСТВЕ R+ х
- 19. а1 = 1,4 а'1 = 1,5 а2 = а‘2 = 1,41 1,42 а3 = а‘3 =
- 20. (∀ а ∈ R) ак ≤ а Любое действительное число разбивает множество рациональных чисел на два
- 21. ак = НГа – нижняя граница числа а а'к = ВГа – верхняя граница числа а
- 22. ДЕЙСТВИЯ НАД ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ Пусть даны действительные числа а и b ак и bк – их
- 23. Суммой положительных действительных чисел а и b называется такое число а + b, которое удовлетворяет следующему
- 24. а = 0,33333… а4 = 0,3333; а4' = 0,3334 b4 = 1,5707; b4' = 1,5708 а4+
- 25. ЗАКОНЫ СЛОЖЕНИЯ Сложение во множестве R+ коммутативно: (∀ а, b ∈ R+) а + b =
- 26. Ассоциативный закон сложения (∀ а, b, с ∈ R+) (а + b) + с = а
- 27. Произведением положительных действительных чисел а и b называется такое число а · b, которое удовлетворяет следующему
- 28. 3,14 ≤ π
- 29. ЗАКОНЫ УМНОЖЕНИЯ 1) коммутативность: (∀ а, b ∈ R+) а · b = b · а
- 30. Дистрибутивный закон умножения относительно сложения (∀ а, b, с ∈ R+) (а + b) · с
- 31. {(ак + bк)· ск} ≤ (а + b) · с {ак·ск + bк·ск} ≤ а·с +
- 32. Разностью двух положительных действительных чисел а и b называется действительное число с = а – b,
- 33. Геометрическая интерпретация действительного числа
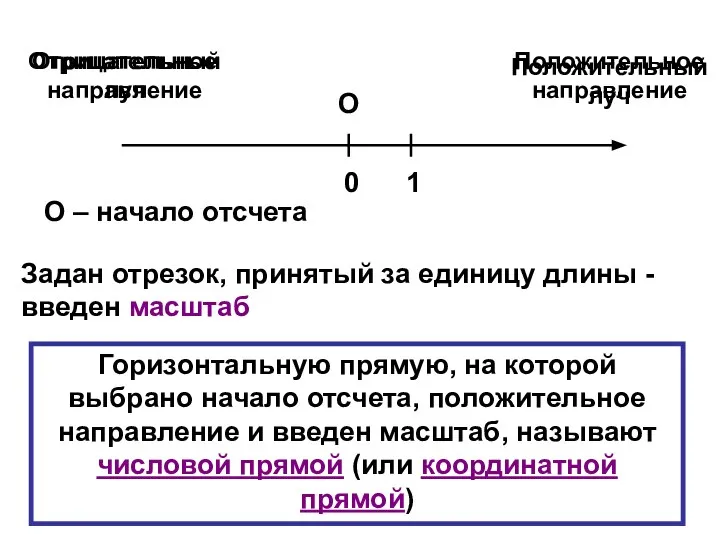
- 34. Отрицательное направление Положительное направление О О – начало отсчета Положительный луч Отрицательный луч Задан отрезок, принятый
- 35. Все точки, изображающие положительные действительные числа, располагаются справа от точки О Числа, расположенные на координатной прямой
- 36. Множество отрицательных действительных чисел обозначают R- R- ∪ R+ ∪ {0} = R Расстояние от начала
- 37. Каждой точке числовой прямой можно поставить в соответствие действительное число по следующему правилу: 1) выбранной точке
- 38. Разным точкам числовой прямой поставлены в соответствие разные числа. Нет ни одного действительного числа, которое не
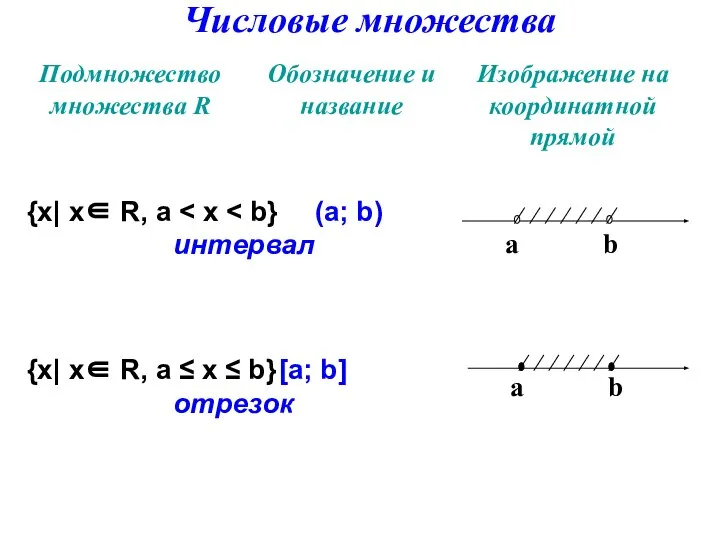
- 39. Числовые множества {х| х∈ R, а интервал {х| х∈ R, а ≤ х ≤ b} [а;
- 40. {х| х∈ R, а полуинтервал {х| х∈ R, а ≤ х полуинтервал
- 41. {х| х∈ R, х ≥ а} [а; +∞) луч {х| х∈ R, х > а} (а;
- 42. {х| х∈ R, х ≤ а} (- ∞; а] луч {х| х∈ R, х луч
- 43. При любом расположении на координатной прямой двух разных точек А(а) и В(b) расстояние d между этими
- 44. Действия над действительными числами Суммой двух действительных чисел называется число, удовлетворяющее условиям: - сумма двух положительных
- 45. Произведением двух действительных чисел называется число, удовлетворяющее условиям: - произведение положительных чисел есть число положительное и
- 46. Вычитание и деление действительных чисел определяется как действия, обратные соответственно сложению и умножению. Вычитание во множестве
- 48. Скачать презентацию





































![{х| х∈ R, х ≤ а} (- ∞; а] луч {х| х∈ R, х луч](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1465798/slide-41.jpg)




 Сформулировать результат выполнения фрагмента (функции) и определить роль переменной – счетчика
Сформулировать результат выполнения фрагмента (функции) и определить роль переменной – счетчика Теория графов
Теория графов Интерактивный плакат: Объём пирамиды
Интерактивный плакат: Объём пирамиды Сложение двузначных чисел урок - сказка
Сложение двузначных чисел урок - сказка  Тригонометрические функции. Тангенс и котангенс
Тригонометрические функции. Тангенс и котангенс Устный счёт
Устный счёт Устные задачи на готовых чертежах. Смежные и вертикальные углы
Устные задачи на готовых чертежах. Смежные и вертикальные углы Вычисление интегралов
Вычисление интегралов Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии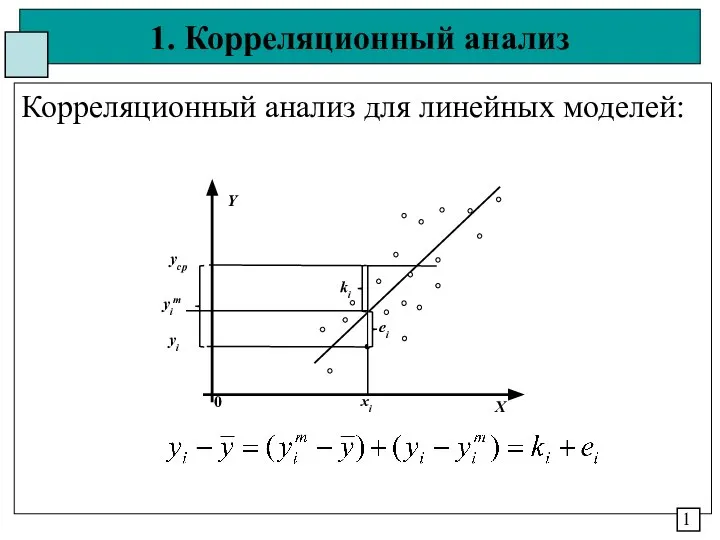 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Аттестационная работа. Эссе. Проектно-исследовательская деятельность на уроках математики в условиях реализации ФГОС
Аттестационная работа. Эссе. Проектно-исследовательская деятельность на уроках математики в условиях реализации ФГОС Одночлены и их свойства
Одночлены и их свойства Квадрат одночлена
Квадрат одночлена Тождества. Переместительное свойство
Тождества. Переместительное свойство Условная оптимизация. Лекция 11
Условная оптимизация. Лекция 11 Адаптивные фильтры. Практическое применение (3)
Адаптивные фильтры. Практическое применение (3) Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Оценки рисков
Оценки рисков Прямоугольный параллелепипед
Прямоугольный параллелепипед Итоговый контрольный тест по геометрии, 7 класс
Итоговый контрольный тест по геометрии, 7 класс Делители и кратные
Делители и кратные Основы математического моделирования в землеустройстве
Основы математического моделирования в землеустройстве Смежные и вертикальные углы
Смежные и вертикальные углы Формализованные методы прогнозирования
Формализованные методы прогнозирования Математичні моделі та методи теорії портфеля
Математичні моделі та методи теорії портфеля Пентамино. Игра-головоломка
Пентамино. Игра-головоломка Обобщающий урок по теме «Соотношения между сторонами и углами треугольника»
Обобщающий урок по теме «Соотношения между сторонами и углами треугольника» Цилиндр
Цилиндр