Дифференциальное исчисление

b).

Аргументу x придадим некоторое приращение :

х 0

f(x 0 )

x 0 +Δx

f(x0+ Δx )

Найдем соответствующее приращение функции:

Если существует предел

то его называют производной функции y = f(x) и обозначают одним из символов:

каждой точке интервала (a; b), называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.

Значение производно функции y = f(x) в точке x0 обозначается одним из символов:

Если функция y = f(x) описывает какой – либо физический процесс, то f ’(x) есть скорость протекания этого процесса – физический смысл производной.

Производной функции в точке  x0 называется предел отношения приращения функции  ∆y к вызвавшему его приращению аргумента ∆x в этой точке при  ∆x→0.

)

x0+Δx

М

М1

f(x0+ Δx )

Через точки М и М1 проведем секущую и обозначим через φ угол наклона секущей.

функции y = f(x) в точке, абсцисса которой равна x.

Если точка касания М имеет координаты (x0; y0 ), угловой коэффициент касательной есть k = f ’(x0 ).

Уравнение прямой с угловым коэффициентом:

Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.

Уравнение касательной

Уравнение нормали

задан закон движения точки: координата x движущейся точки – это известная функция времени x(t).
В течение интервала времени от t0 до t0+∆t точка перемещается на расстояние  

Средняя скорость точки находится по формуле:   
При  ∆t→0 значение средней скорости стремится к определённой величине, которая в физике называется мгновенной скоростью  материальной точки в момент времени  .
Следовательно, для мгновенной скорости можно записать формулу 
Если сравнить эту формулу с формулой производной, то можно сделать вывод, что cкорость – это производная координаты по времени 

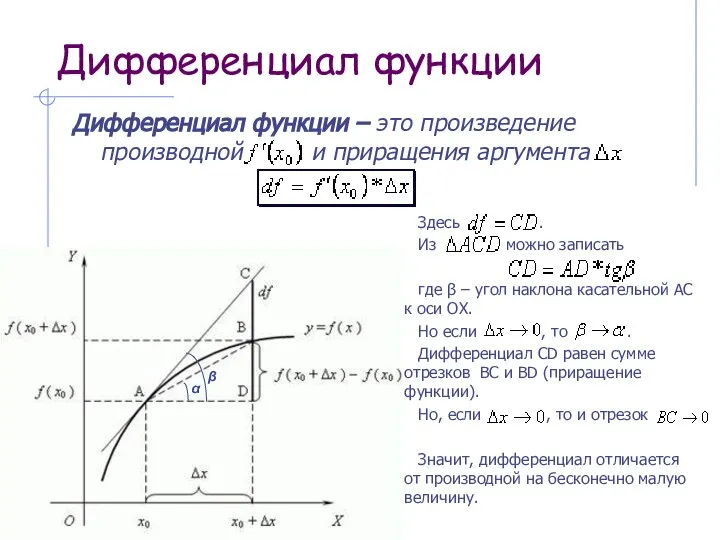
Механический смысл производной

АС к оси ОХ.
Но если  , то  .
Дифференциал CD равен сумме отрезков  BС и BD (приращение функции).
Но, если , то и отрезок
Значит, дифференциал отличается от производной на бесконечно малую величину.

Дифференциал функции – это произведение производной  и приращения аргумента

β

α

интервале (a; b) функции, С – постоянная.

тогда y = f(φ(x)) – сложная функция с промежуточным аргументом u и независимым аргументом x.

Теорема

Это правило остается в силе, если промежуточных аргументов несколько: