Содержание
- 2. § 1. Понятие функции двух переменных.
- 3. Пусть x, y – две независимые друг от друга переменные. Графически пару независимых переменных (x, y)
- 4. Опр. Если каждой точке M(x, y) из множества D по некоторому закону f ставится в соответ-ствие
- 5. Геометрическим изображением функции двух переменных является некоторая поверхность в трехмерном пространстве.
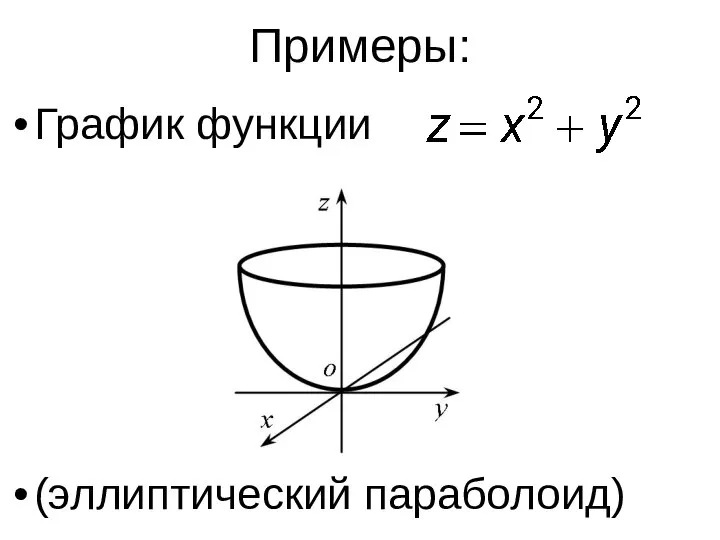
- 6. Примеры: График функции (эллиптический параболоид)
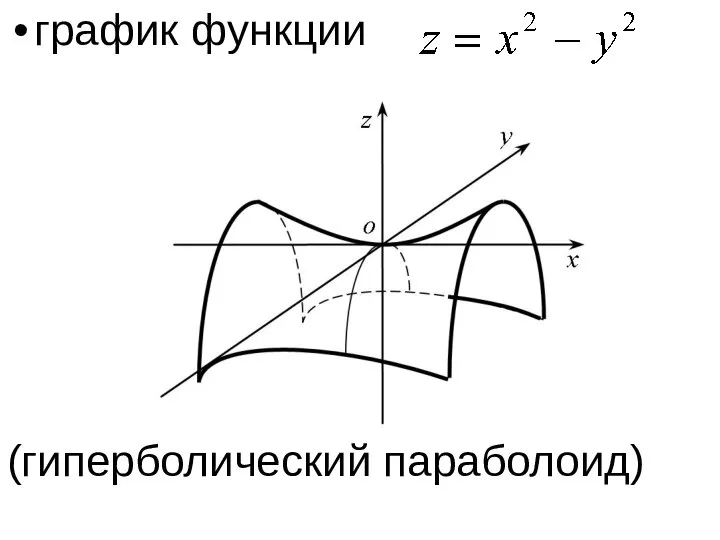
- 7. график функции (гиперболический параболоид)
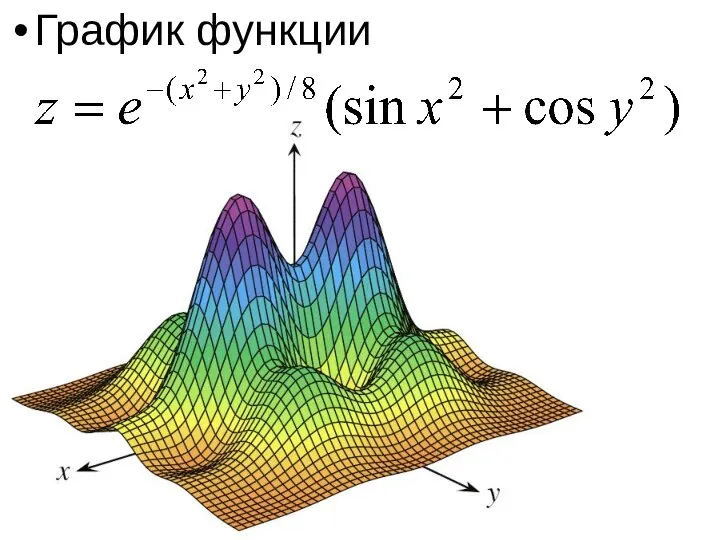
- 8. График функции
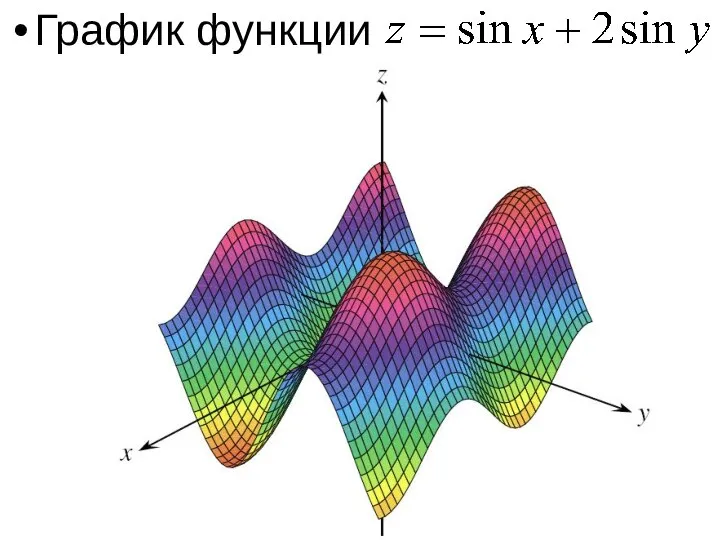
- 9. График функции
- 10. Опр. Областью определения функции z = f(x, y) называется множество D точек M(x, y), в которых
- 11. Примеры
- 12. Графическое изображение области определения функции. Пример. Построим область определения функции
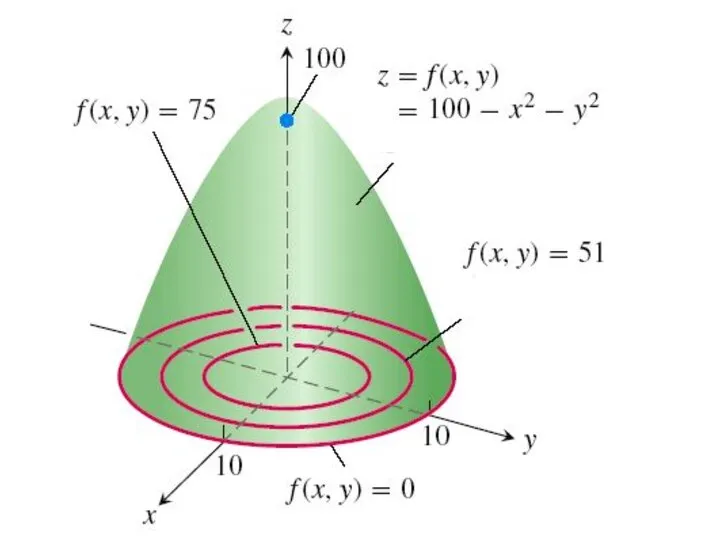
- 14. Линии уровня Опр. Множество точек плоскости таких, что функция f(x, y) принимает в них одно и
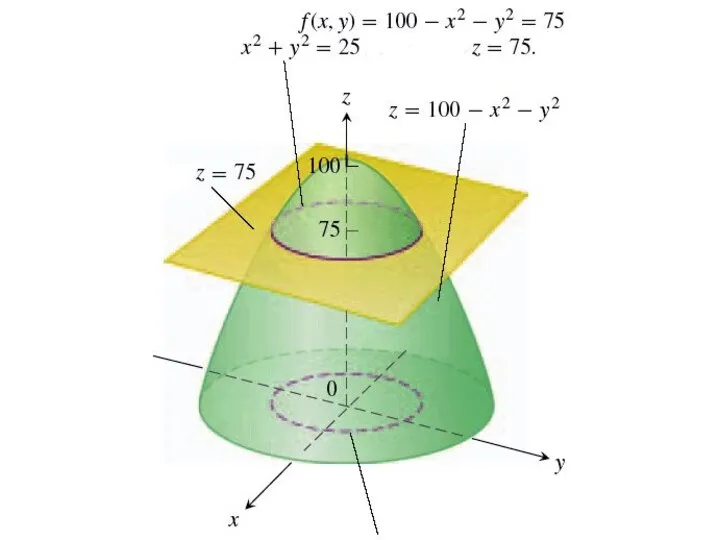
- 19. Построение графика функции двух переменных Рассмотрим пример построения графика функции
- 20. Зафиксируем какое-нибудь значение этой функции, например, z = 75. Тем самым мы определили в пространстве плоскость
- 22. Находя множество линий уровня, строим весь график.
- 24. § 2. Понятие функции трех и более переменных. Всякая упорядоченная совокупность действительных чисел (x1, x2, …,
- 25. Опр. Если каждой точке M(x1, x2, …, xn) из области D по некоторому закону f ставится
- 26. Примеры
- 27. Опр. Множество точек пространства, в которых функция трех переменных f(x, y, z) принимает одно и то
- 29. § 3. Предел и непрерывность функции нескольких переменных
- 30. Опр. Число A называется пределом функции z = f(x, y) в точке M0(x0, y0), если для
- 31. Опр. Функция z = f(x, y) называется непрерывной в точке M0(x0, y0), если функция z =
- 32. Аналогичные определения имеют место и для функции u = f(x1, x2, …, xn) в случае произвольного
- 33. Если в какой – либо точке условие непрерывности не выполняется, то эта точка называется точкой разрыва
- 34. 1. Функция z = f(x, y) не определена в точке M0(x0, y0). 2. Не существует предел
- 35. § 4. Частные производные функции нескольких переменных
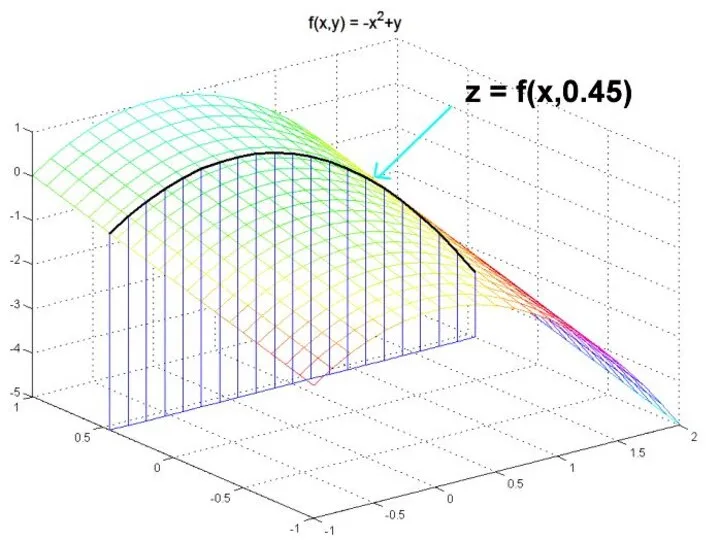
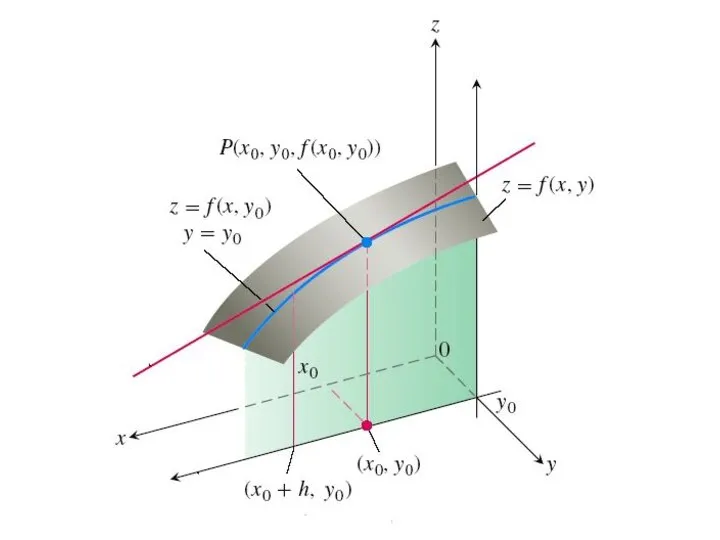
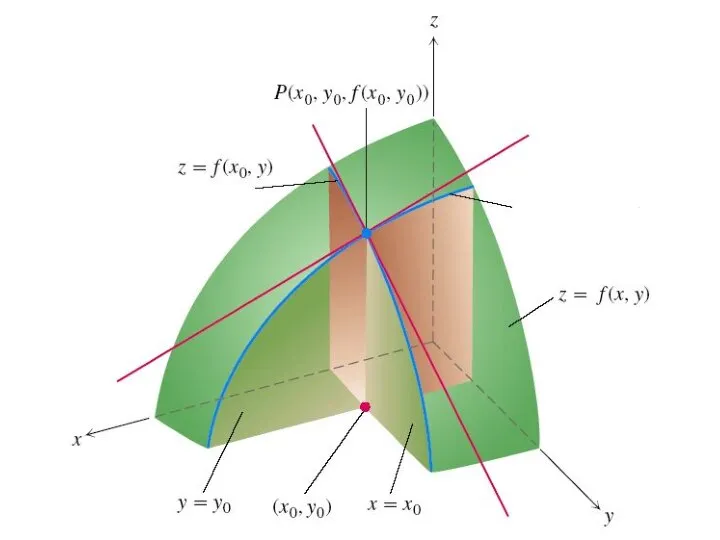
- 45. Пусть z = f(x, y) – функция двух переменных. Дадим независимой переменной x приращение Δx, оставляя
- 46. Аналогично, если независимой переменной y дадим приращение Δy, оставляя при этом неизменной переменную x, то функция
- 47. Опр. Частной производной по x от функции z называется предел отношения частного приращения Δxz к приращению
- 48. Таким образом, по определению,
- 49. Аналогично определяется частная производная от функ-ции z = f(x, y) по переменной y : Обозначается одним
- 50. В общем случае частной производной первого порядка функции u = f(x1, x2, …, xn) по переменной
- 51. Т.к. при вычислении частных производных все переменные, кроме одной, считают постоянными, то для частных производных сохранаяются
- 52. Пример. Найти частные производные функции
- 53. Решение. Полагая y = const, находим
- 54. Полагая x = const, находим
- 55. Пример. Найти значения частных производных функции в точке M(1, –1, 0).
- 56. Решение. Полагая y = const, z = const, находим
- 57. Аналогично находим
- 58. Предположим, что функция z = f(x, y) имеет непрерывные частные производные
- 59. Эти производные в свою очередь являются функциями независимых переменных x и y. Будем называть и частными
- 60. Частными производными 2-го порядка называются частные производные от частных производных 1-го порядка. Для функции z =
- 62. В общем случае смешанные частные производные могут не совпадать, однако для них справедлива теорема: Теорема. Если
- 63. Частными производными n–го порядка называются частные производные от частных производных (n – 1)–го порядка. Их обозначают
- 64. Частные производные любого порядка, взятые по различным переменным, называются смешанными.
- 65. Пример. Найти частные производные 2-го порядка функции
- 66. Решение. Последовательно находим
- 73. Скачать презентацию










































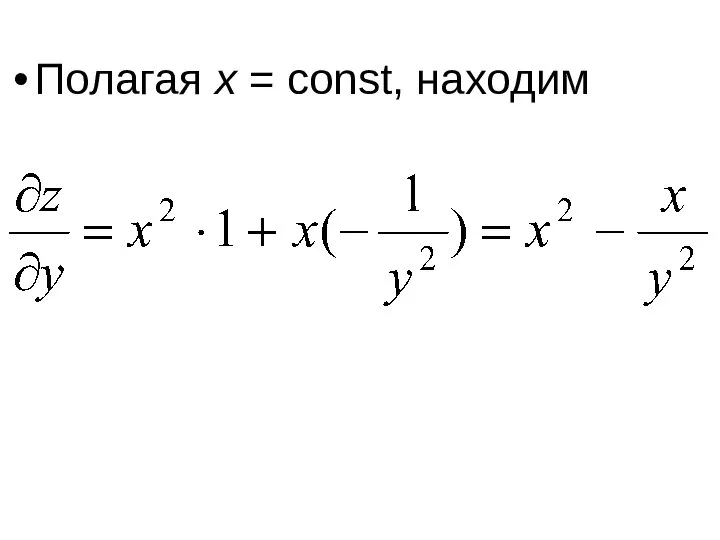


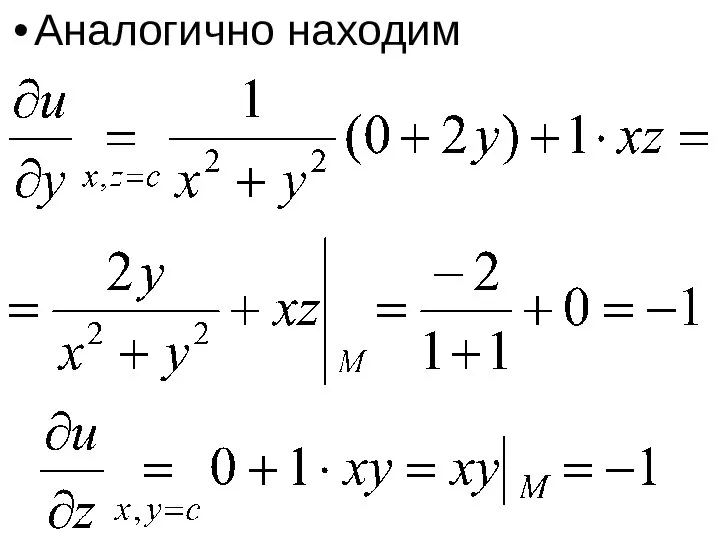









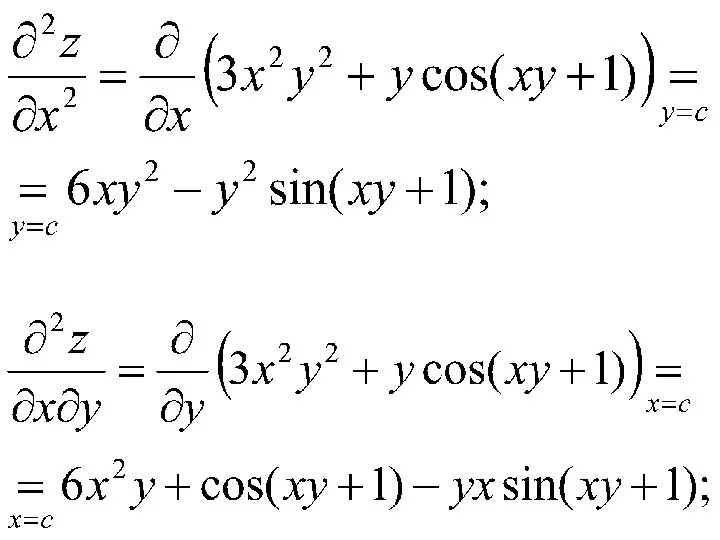




 Кто хочет стать математиком
Кто хочет стать математиком Закон больших чисел и центральная предельная теорема
Закон больших чисел и центральная предельная теорема Углы и диагонали многоугольников. 5 класс
Углы и диагонали многоугольников. 5 класс Формулы середины отрезка и расстояния между двумя точками
Формулы середины отрезка и расстояния между двумя точками Площадь криволинейной трапеции
Площадь криволинейной трапеции Схема Бернулли
Схема Бернулли Основні види моделювання. Формальні методи побудови моделей
Основні види моделювання. Формальні методи побудови моделей Теорема Виета
Теорема Виета Функциональное зонирование
Функциональное зонирование Решение систем уравнений методом введения новой переменной (9 класс)
Решение систем уравнений методом введения новой переменной (9 класс) Фунцияның туындысы мен дифференциалын қолдану
Фунцияның туындысы мен дифференциалын қолдану Теорема Пифагора
Теорема Пифагора Определение высоты здания
Определение высоты здания Число π (пи)
Число π (пи) Случаи вычитания 14 -
Случаи вычитания 14 - Натуральные числа
Натуральные числа Теорема Пифагора и ее применение при решении различных задач
Теорема Пифагора и ее применение при решении различных задач Признаки равенства треугольников
Признаки равенства треугольников Презентация по математике "Сложение дробей с одинаковыми знаменателями (5 класс)" - скачать
Презентация по математике "Сложение дробей с одинаковыми знаменателями (5 класс)" - скачать  Деление дробей. 8 класс
Деление дробей. 8 класс Третий признак равенства треугольников
Третий признак равенства треугольников Математика. Что такое периметр?
Математика. Что такое периметр? Ловушка фиктивных переменных
Ловушка фиктивных переменных Архитектура и геометрия
Архитектура и геометрия Презентация по математике "Нахождение наибольшего общего делителя чисел" - скачать
Презентация по математике "Нахождение наибольшего общего делителя чисел" - скачать  Пустыня ошибок
Пустыня ошибок Связь между суммой и слагаемыми
Связь между суммой и слагаемыми Использование ИКТ в обучении геометрии
Использование ИКТ в обучении геометрии