Содержание
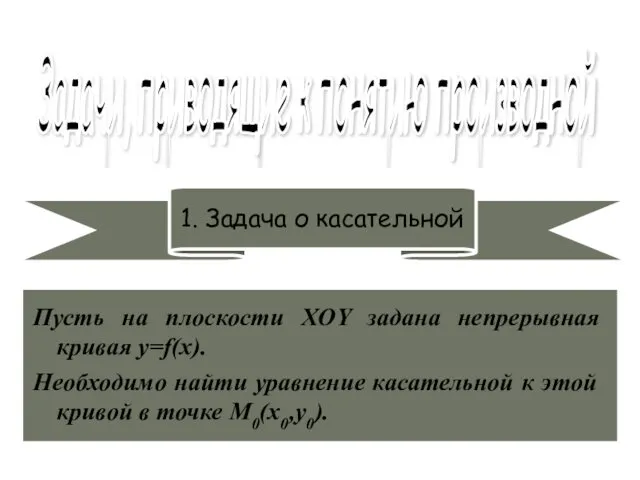
- 2. Задачи, приводящие к понятию производной 1. Задача о касательной Пусть на плоскости XOY задана непрерывная кривая
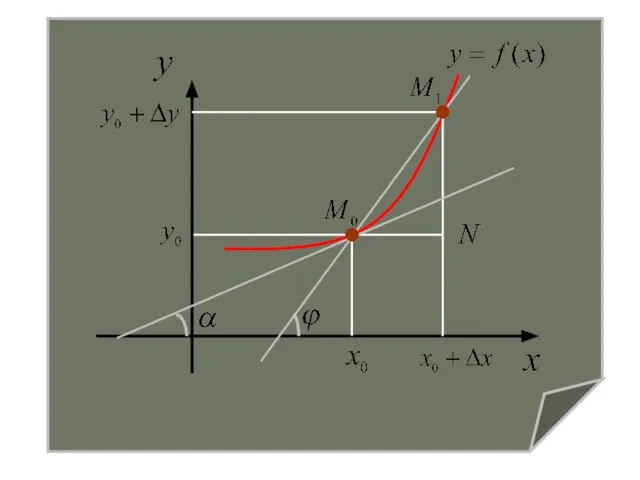
- 3. Дадим аргументу x0 приращение Δx и перейдем на кривой от точки M0(x0, f(x0)) к точке M1(x0+Δx,
- 5. Уравнение прямой, проходящей через точку M0 имеет вид: Рассмотрим прямоугольный треугольник M0M1N: - угловой коэффициент секущей
- 6. Тогда угловой коэффициент касательной к кривой в точке M0 :
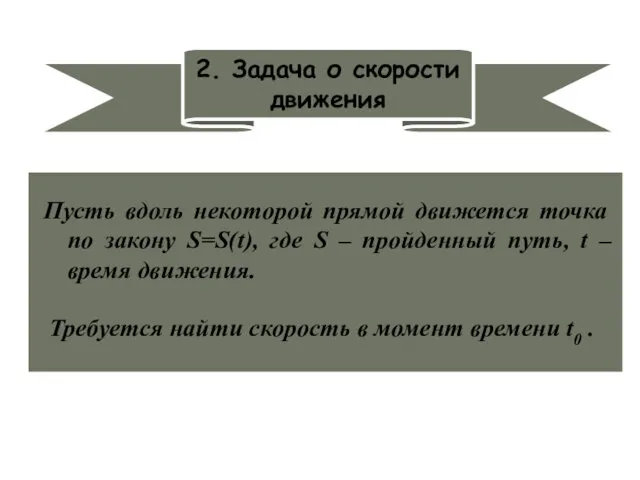
- 7. 2. Задача о скорости движения Пусть вдоль некоторой прямой движется точка по закону S=S(t), где S
- 8. Тогда за промежуток времени Δt средняя скорость составит: Чем меньше Δt, тем лучше средняя скорость характеризует
- 9. Поэтому под скоростью точки в момент времени t0 понимают:
- 10. Определение производной Пусть функция y=f(x) определена на промежутке Х. Выберем точку Дадим аргументу x приращение Δx,
- 11. Производной функции y=f(x) называется предел отношения приращения функции к приращению независимого аргумента, когда приращение аргумента стремится
- 12. Обозначения производной: Нахождение производной функции называется дифференцированием. Если функция имеет конечную производную в некоторой точке, то
- 13. Вернемся к рассматриваемым задачам. Из задачи о касательной вытекает Производная f / (x0) есть угловой коэффициент
- 14. Тогда уравнение касательной к кривой в данной точке будет иметь вид:
- 15. Из задачи о скорости движения вытекает Производная пути по времени S / (t0) есть скорость точки
- 16. ТЕОРЕМА Если функция y=f(x) дифференцируема в точке x0, то она непрерывна в этой точке.
- 17. Непрерывность функции является необходимым, но не достаточным условием дифференцируемости функции. Если функция имеет непрерывную производную на
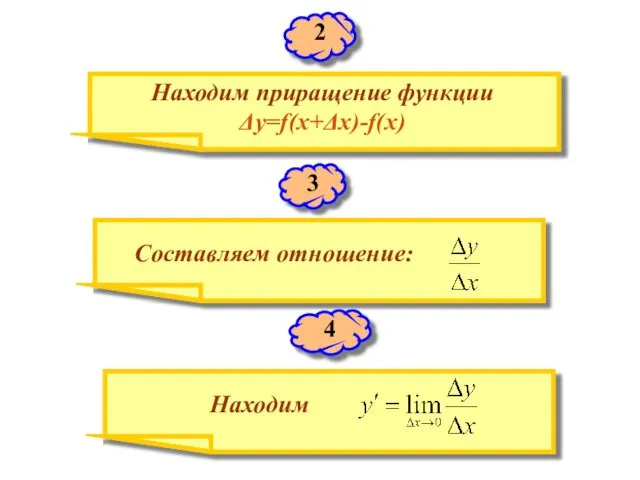
- 18. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Производная функции может быть найдена по схеме: Дадим аргументу х приращение Δх и
- 19. Находим приращение функции Δy=f(x+Δx)-f(x) 2 3 Составляем отношение: 4 Находим
- 20. ПРИМЕР. Найдем производную функции Дадим аргументу х приращение Δх и найдем значение функции y+Δy: 1 2
- 21. 3 Составляем отношение
- 22. Находим 4 Полученный результат является частным случаем производной от степенной функции Можно показать, что в общем
- 23. производная степенной функции
- 24. Таблица производных основных элементарных функций. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
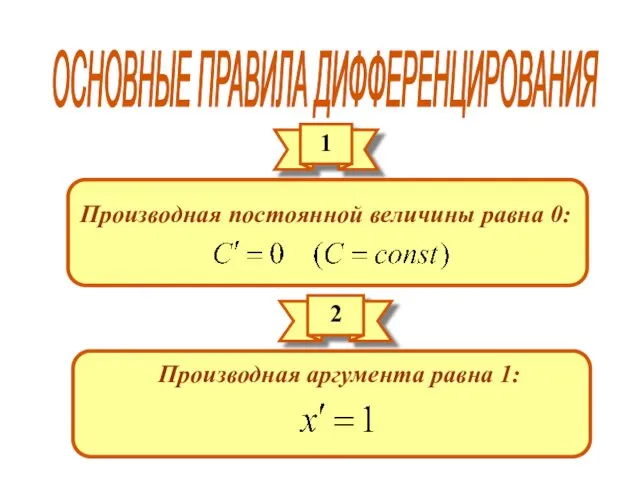
- 25. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ 1 Производная постоянной величины равна 0: 2 Производная аргумента равна 1:
- 26. 3 Производная алгебраической суммы (разности) конечного числа дифференцируемых функций равна сумме (разности) производных этих функций:
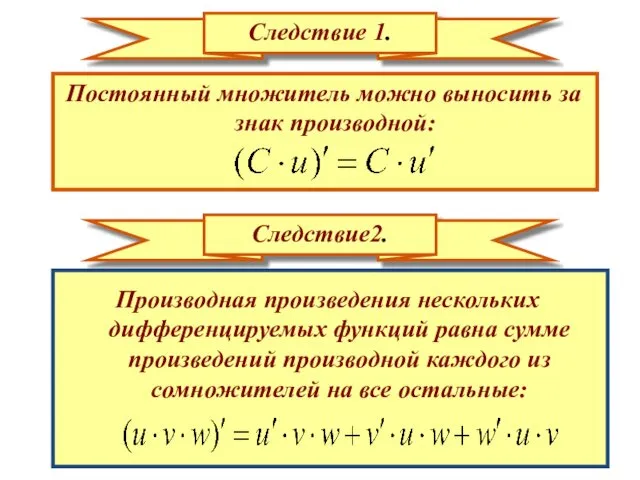
- 27. Следствие 1. Постоянный множитель можно выносить за знак производной: Следствие2. Производная произведения нескольких дифференцируемых функций равна
- 28. 5 Производная частного двух дифференцируемых функций находится по формуле:
- 29. ПРИМЕРЫ. 1 Найти производную функции и вычислить ее значение в точке х=1.
- 30. Решение. Находим значение производной в точке х=1:
- 31. 2 Найти производную функции и вычислить ее значение в точке х=1.
- 32. Решение. Находим значение производной в точке х=1:
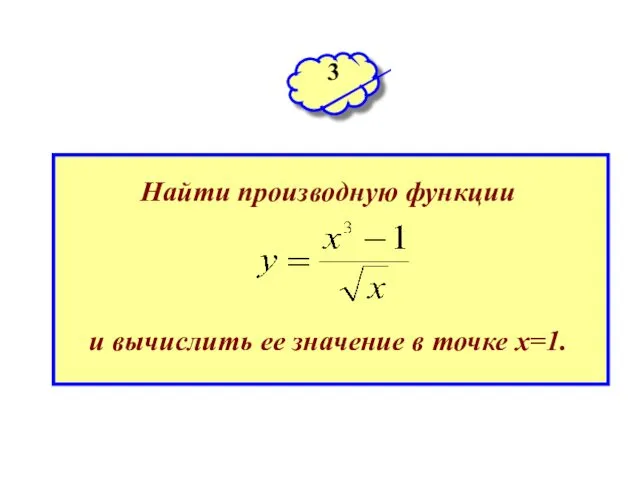
- 33. 3 Найти производную функции и вычислить ее значение в точке х=1.
- 34. Решение. Находим значение производной в точке х=1:
- 35. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ Пусть переменная y есть функция от переменной u, y=f(u). И пусть переменная u
- 36. ТЕОРЕМА Если y=f(u), u=φ(x) – дифференцируемые функции своих аргументов, то производная сложной функции существует и равна
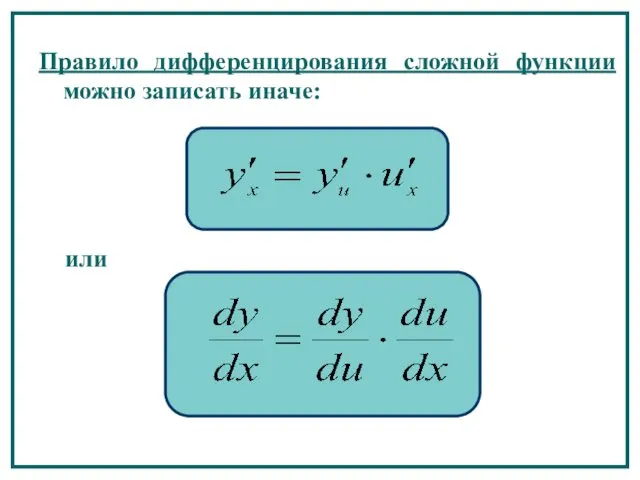
- 37. Правило дифференцирования сложной функции можно записать иначе: или
- 38. Примеры. 1 Найти производные сложных функций:
- 39. Решение:
- 40. 2
- 41. Решение:
- 43. ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ Пусть y=f(x) – дифференцируемая и монотонная функция на промежутке Х. Если переменную y
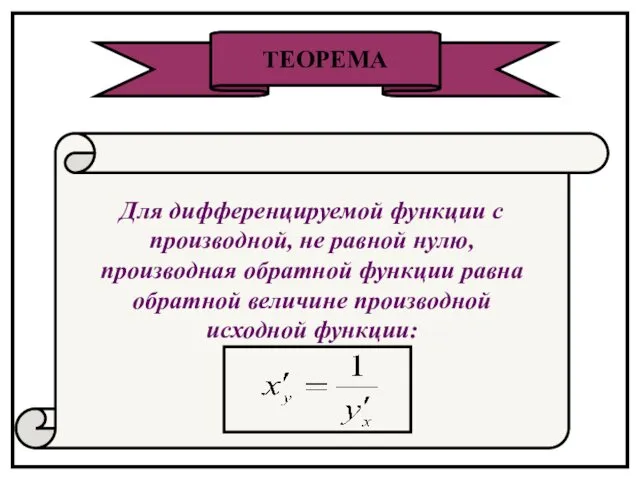
- 44. ТЕОРЕМА Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной
- 45. ПОНЯТИЕ ДИФФЕРЕНЦИАЛА ФУНКЦИИ Пусть функция y=f(x) определена на промежутке Х и дифференцируема в некоторой окрестности точки
- 46. Где - бесконечно малая величина при Следовательно, Таким образом, приращение функции состоит из двух слагаемых: 1.
- 47. Дифференциалом функции называется главная, линейная относительно Δх, часть приращения функции, равная произведению производной на приращение независимой
- 48. Пример. Найти приращение и дифференциал функции при х=10 и Δх=0.1
- 49. Решение: при х=10 и Δх=0.1
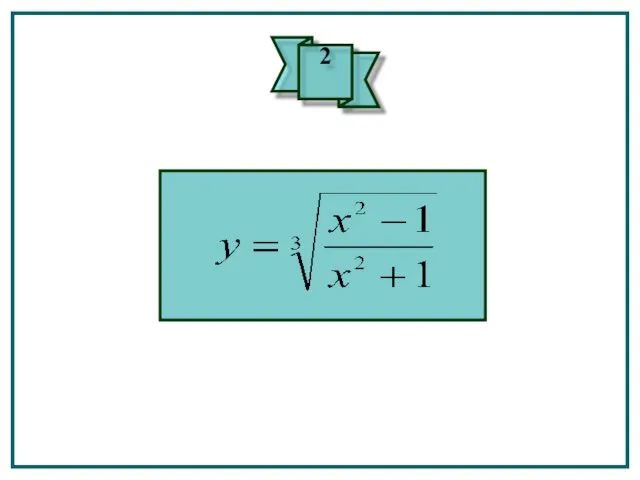
- 50. Пример. Найти дифференциал функции
- 51. Решение: Следовательно, дифференциал независимой переменной равен приращению этой переменной:
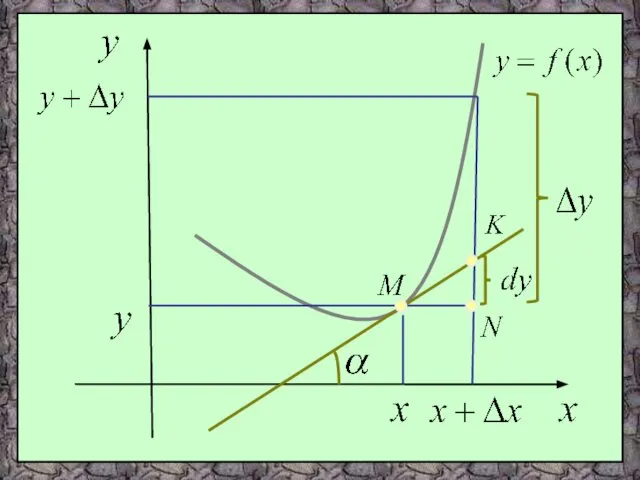
- 52. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА Выберем на графике функции y=f(x) произвольную точку М(x,y). Дадим аргументу х приращение Δх.
- 55. Скачать презентацию





































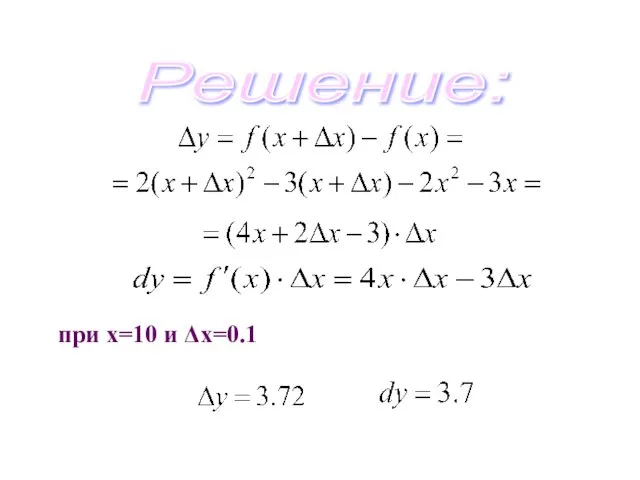



 Презентация на тему Число 4 цифра 4
Презентация на тему Число 4 цифра 4 Операция факториалов и история появления его в положительных рядах Выполнил: Павлов В. А. Проверила: Хлынова Т. В.
Операция факториалов и история появления его в положительных рядах Выполнил: Павлов В. А. Проверила: Хлынова Т. В. Решение логических задач для 5-9 классов
Решение логических задач для 5-9 классов Линейное уравнение с одной переменной. Урок алгебры с применением ИКТ. 7 класс
Линейное уравнение с одной переменной. Урок алгебры с применением ИКТ. 7 класс Назначение и описание критерия Фишера
Назначение и описание критерия Фишера «Забавная арифметика» Выполнил Новиков Антон, 5 класс школы № 96 города Краснодара Руководитель Сосна Ольга Александровна
«Забавная арифметика» Выполнил Новиков Антон, 5 класс школы № 96 города Краснодара Руководитель Сосна Ольга Александровна Аттестационная работа. Методическая разработка по выполнению проекта по математике «Некоторые замечательные кривые»
Аттестационная работа. Методическая разработка по выполнению проекта по математике «Некоторые замечательные кривые» Автор: учитель математики МБОУ СОШ №38, г. Озерска, Челябинской области Комарова Наталья Алексеевна Решение систем уравнений вт
Автор: учитель математики МБОУ СОШ №38, г. Озерска, Челябинской области Комарова Наталья Алексеевна Решение систем уравнений вт Прямоугольный треугольник. 7 класс
Прямоугольный треугольник. 7 класс Логические задачи. Зрительные иллюзии
Логические задачи. Зрительные иллюзии Габриэль Крамер
Габриэль Крамер Решение задач
Решение задач Нахождение квадратных корней
Нахождение квадратных корней Треугольники. Центр тяжести
Треугольники. Центр тяжести Презентация по математике "Правильные многогранники в четырехмерном пространстве" - скачать
Презентация по математике "Правильные многогранники в четырехмерном пространстве" - скачать  Измерение углов.Транспортир. 5 класс
Измерение углов.Транспортир. 5 класс Уравнения. 5 класс
Уравнения. 5 класс Уравнения в школьном курсе средней школы. 5-6 класс
Уравнения в школьном курсе средней школы. 5-6 класс Тестовые задания в формате ГИА. К уроку алгебры в 8 классе
Тестовые задания в формате ГИА. К уроку алгебры в 8 классе Задачи по планиметрии на ЕГЭ
Задачи по планиметрии на ЕГЭ Метод координат. Решение задач
Метод координат. Решение задач Основы анализа данных. Регрессионный анализ. (Лекция 6)
Основы анализа данных. Регрессионный анализ. (Лекция 6) Аттестационная работа. Методическая разработка по выполнению проектно-исследовательской работы. Искусство оригами и математика
Аттестационная работа. Методическая разработка по выполнению проектно-исследовательской работы. Искусство оригами и математика Презентация по математике "Осевая и центральная симметрии" -
Презентация по математике "Осевая и центральная симметрии" -  Решение задача на совместную работу. 6 класс
Решение задача на совместную работу. 6 класс Преобразование тригонометрического выражения
Преобразование тригонометрического выражения Геометрия. Основные фигуры
Геометрия. Основные фигуры Проект ученицы 10 класса «А» Ксенафонтовой Лены на тему:
Проект ученицы 10 класса «А» Ксенафонтовой Лены на тему: