Дискретная математика Глава 1. Множества и отношения

множество натуральных чисел; < - отношение «меньше» на N.

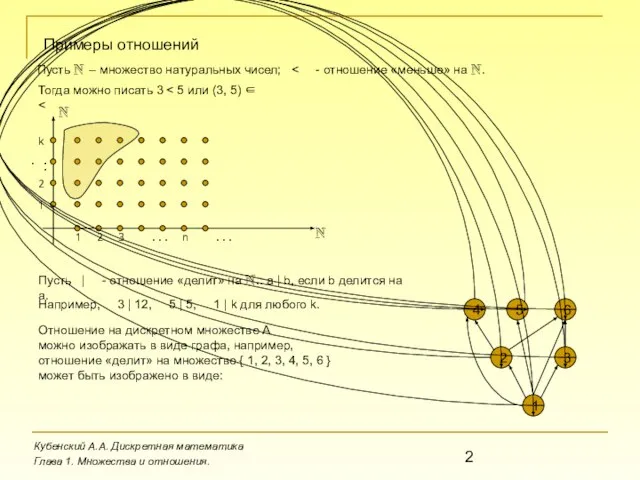
Тогда можно писать 3 < 5 или (3, 5) ∈ <

Пусть | - отношение «делит» на N.: a | b, если b делится на a.

Например, 3 | 12, 5 | 5, 1 | k для любого k.

Отношение на дискретном множестве A можно изображать в виде графа, например, отношение «делит» на множестве { 1, 2, 3, 4, 5, 6 } может быть изображено в виде:

можно выполнять все теоретико-множественные операции, поскольку каждое отношение – это некоторое множество.

Пусть на множестве натуральных чисел N заданы отношения «меньше» (<), «равны» (=) и «делит» (|). Тогда можно рассмотреть следующие отношения:

< ∪ =

- в результате получается отношение ≤

< ∩ |

- в результате получается отношение «делит, но не равно»

| \ =

- в результате также получается отношение «делит, но не равно»

<

(дополнение до N x N) - в результате получается отношение ≥

Две специфические операции над отношениями:

Если R1 : A → B, а R2 : B → C, то отношением R2 ° R1 (композиция R1 и R2) будет называться отношение R = R2 ° R1, R : A → C, R = { (a, c) | ∃b∈B: (a, b) ∈ R1, (b, c) ∈ R2 }

Если R : A → B, то отношением R-1 (обратное к R отношение) будет называться отношение R-1 : B → A, R-1 = { (b, a) | (a, b) ∈ R }

Например:

| ° <

a (| ° <) b, если найдется c такое, что a < c и c | b. Это верно для любых a < b, поэтому (| ° <) = (<)

<-1

a (<-1) b, если b < a, поэтому (<-1) = (>)

отношениями

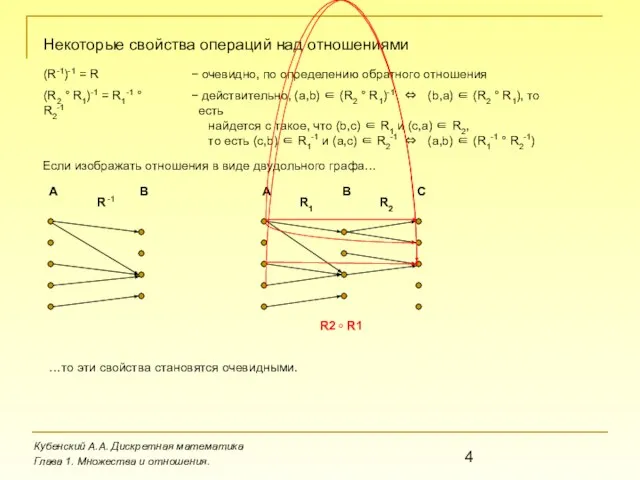
(R-1)-1 = R

очевидно, по определению обратного отношения

(R2 ° R1)-1 = R1-1 ° R2-1

действительно, (a,b) ∈ (R2 ° R1)-1 ⇔ (b,a) ∈ (R2 ° R1), то есть найдется c такое, что (b,c) ∈ R1 и (c,a) ∈ R2, то есть (c,b) ∈ R1-1 и (a,c) ∈ R2-1 ⇔ (a,b) ∈ (R1-1 ° R2-1)

Если изображать отношения в виде двудольного графа…

A

B

R

-1

…то эти свойства становятся очевидными.

таково, что для каждого a∈A существует не более одного b∈B такого, что aRb, то отношение R называется функцией из A в B.

При этом элемент b, если он существует, называется образом элемента a, а элемент a – прообразом элемента b.

Если для каждого элемента a∈A существует его образ, то говорят, что функция задана на A.

Ядро отношения

Если задано отношение R : A → B, то отношение ker R = R-1 ◦ R называется ядром отношения R.

ker R – это отношение из A и A.

Если F – функция из A и B, то (a1, a2) ∈ ker F, если элементы a1 и a2 имеют один и тот же образ.

отношение R на A.

Рефлексивность

∀a∈A aRa

Симметричность

∀a,b∈A aRb ⇒ bRa

Транзитивность

∀a,b,c∈A aRb, bRc ⇒ aRc

Рассматривают еще:

Антирефлексивность

∀a∈A aRa

Антисимметричность

∀a,b∈A aRb, bRa ⇒ a = b

Асимметричность

∀a,b∈A aRb ⇒ bRa

Если отношение рефлексивно, симметрично и транзитивно, то оно называется отношением эквивалентности.

Если отношение антирефлексивно, асимметрично и транзитивно, то оно называется отношением строгого порядка.

Если отношение рефлексивно, антисимметрично и транзитивно, то оно называется отношением нестрогого порядка.

Нестрогий порядок P называется полным (или линейным), если ∀a,b∈A aPb или bPa. Строгий порядок P называется полным, если для любых различных a и b верно aPb или bPa. Если порядок не полный, то он называется частичным.

на множестве целых чисел:

антирефлексивно;

асимметрично;

транзитивно;

⇒ это отношение строгого линейного порядка;

Пусть задано некоторое множество A, тогда отношение ⊂ есть отношение на его булеане 2A. Оно:

рефлексивно;

антисимметрично;

транзитивно;

⇒ это отношение нестрогого частичного порядка;

Пусть задано некоторое число M, тогда отношение ≡ (mod M) есть отношение на множестве целых чисел. Оно:

рефлексивно;

симметрично;

транзитивно;

⇒ это отношение эквивалентности;

Отношение | (делит) на множестве натуральных чисел:

рефлексивно;

антисимметрично;

транзитивно;

⇒ это отношение нестрогого частичного порядка;

Отношение «взаимно просты» на множестве натуральных чисел:

антирефлексивно;

симметрично;

множества M конечное или счетное семейство { Mi } называется покрытием M, если

Покрытие { Mi } называется разбиением M, если множества Mi дизъюнктны: Mi ∩ Mj = ∅ при i ≠ j

Пусть N+ - множество натуральных чисел, больших единицы, а Ni – множество натуральных чисел, делящихся на i. Тогда семейство образует покрытие N+.

Пусть для заданного m Mi – множество целых чисел n таких, что n ≡ i mod m. Тогда семейство образует разбиение множества всех целых чисел.

Теорема: отношение эквивалентности на некотором множестве M порождает его разбиение на классы эквивалентности – множества элементов, эквивалентных между собой.

Если R – отношение эквивалентности, то мы говорим, что a эквивалентно b, если aRb.

Ясно, что можно говорить о множествах элементов, эквивалентных между собой, поскольку отношение эквивалентности рефлексивно, симметрично и транзитивно.

Ясно, что классы эквивалентности образуют покрытие множества, поскольку каждый элемент множества эквивалентен, по крайней мере, самому себе (по рефлексивности).

Ясно, что классы эквивалентности не пересекаются, поскольку любой элемент, принадлежащий двум разным классам, будет эквивалентен всем элементам как первого, так и второго класса (по транзитивности).

Значит, классы эквивалентности образуют разбиение множества M, и теорема доказана.

Отношение тождественности.

Пусть A – произвольное множество; I – отношение тождественности на нем: aIb тогда и только тогда, когда a и b – один и тот же элемент. Классы эквивалентности, порожденные этим отношением – это все одноэлементные множества, содержащие элементы множества A.

Пример 2. Отношение сравнимости по заданному модулю.

Пусть N – множество натуральных чисел; Rm – отношение на нем: aRmb тогда и только тогда, когда a ≡ b mod m. Классы эквивалентности, порожденные этим отношением – это подмножества натуральных чисел, имеющих один и тот же остаток при делении на m.

Пример 3. Ядро функции.

Пусть F – некоторая функция; F : A → B; ker F – ядро этой функции. Если функция определена на A, то ker F – отношение эквивалентности. Классы эквивалентности, порожденные этим отношением – это подмножества элементов A, имеющих один и тот же образ.

множестве A. Будем говорить, что c – нижняя граница для элементов a и b, если c a и c b.

Аналогично, будем говорить, что c – верхняя граница для элементов a и b, если a c и b c.

Будем говорить, что c – нижняя грань для элементов a и b, если c – наибольшая нижняя граница этих элементов, то есть для любой нижней границы d элементов a и b d c. Обозначение: c = inf (a, b).

Аналогично, c – верхняя грань для элементов a и b, если c – наименьшая верхняя граница этих элементов, то есть для любой верхней границы d элементов a и b c d. Обозначение: c = sup (a, b).

Кубенский А.А. Дискретная математика

Глава 1. Множества и отношения.

Теорема: если нижняя грань для заданных двух элементов существует, то только одна.

Доказательство: пусть c и d – две нижние грани для a и b. Тогда c d и d c. Но, поскольку отношение - антисимметрично, то c и d – один и тот же элемент.

1. Множества и отношения.

Пример 1. Отношение сравнения чисел ≥

Пусть ≥ - отношение «больше или равно» на множестве целых чисел. Для любых двух чисел a и b существуют их верхняя и нижняя грани. inf(a,b) = max(a,b); sup(a,b) = min(a,b)

Пример 2. Отношение включения множеств ⊂

Пусть ⊂ - отношение «есть подмножество» на булеане некоторого множества U. Для любых двух множеств A и B существуют их верхняя и нижняя грани. inf(A,B) = A ∩ B; sup(A,B) = A ∪ B.

Пример 3. Отношение делимости

Пусть | - отношение «делит» на множестве натуральных чисел N. Для любых двух чисел a и b существуют их верхняя и нижняя грани. inf(a,b) = НОД(a,b); sup(a,b) = НОК(a,b).