Содержание
- 2. “Геометрія володіє двома скарбами. Один з них - теорема Піфагора, а другий – поділ відрізка в
- 3. Зміст З найдавніших часів. Піфагор та його школа. Різні доведення теореми Піфагора: метод розкладання на рівновеликі
- 4. З найдавніших часів Історія теореми Піфагора починається набагато раніше до Піфагора. Відомості про неї говорять про
- 5. З найдавніших часів В математичній книзі Чу-пей у давньому Китаї так говориться про трикутник зі сторонами
- 6. З найдавніших часів Зараз всі погоджуються з тим, що ця теорема не була відкрита Піфагором, проте,
- 7. “Віслюків міст” В найдавніші часи доведення теореми Піфагора вважалося дуже складним і опанувати його могли далеко
- 8. Піфагор Самоський В VI столітті до н.е. у сім’ї золотих справ майстра Мнесарха народився син. У
- 9. Піфагор та його школа Пройшло кілька років, і за порадою свого вчителя Піфагор вирішує продовжити навчання
- 10. Піфагор та його школа До цього періоду відноситься подія, яка змінила все його майбутнє життя. Помер
- 11. Піфагор та його школа Заслугою піфагорійців було висування думки про кількісні закономірності розвитку світу, що сприяло
- 12. Метод розкладання на рівновеликі площі Формулювання теореми Піфагора в давнину: Сума площ квадратів, побудованих на катетах
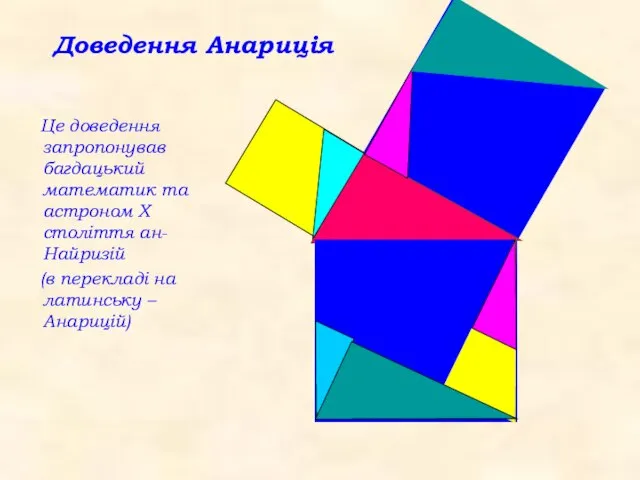
- 13. Доведення Анариція Це доведення запропонував багдацький математик та астроном Х століття ан-Найризій (в перекладі на латинську
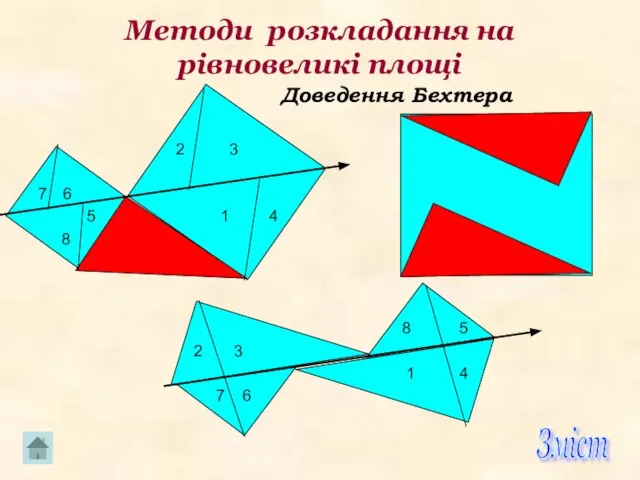
- 14. Методи розкладання на рівновеликі площі Доведення Епштейна Його перевага полягає в тому що квадрати, побудовані на
- 15. Методи розкладання на рівновеликі площі 2 3 6 5 1 4 8 8 5 2 3
- 16. Метод доповнення Поряд з методом розкладання на рівновеликі площі можна навести приклади доведень за допомогою віднімання
- 17. Алгебраїчні доведення В деяких випадках для доведення теореми Піфагора використовують алгебраїчні тотожності. Найстаріше з таких доведень
- 18. Метод подібності Доведення теореми Піфагора методом подібності вперше з'явилося у Бхаскари (ХІІ ст.), також воно є
- 19. Векторний метод Теорема Піфагора може бути доведена за допомогою векторів. Наведемо це доведення А С В
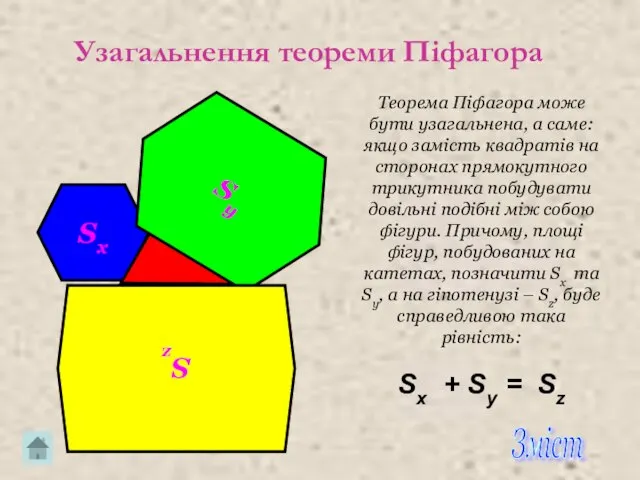
- 20. Узагальнення теореми Піфагора Sx Sy Sz Теорема Піфагора може бути узагальнена, а саме: якщо замість квадратів
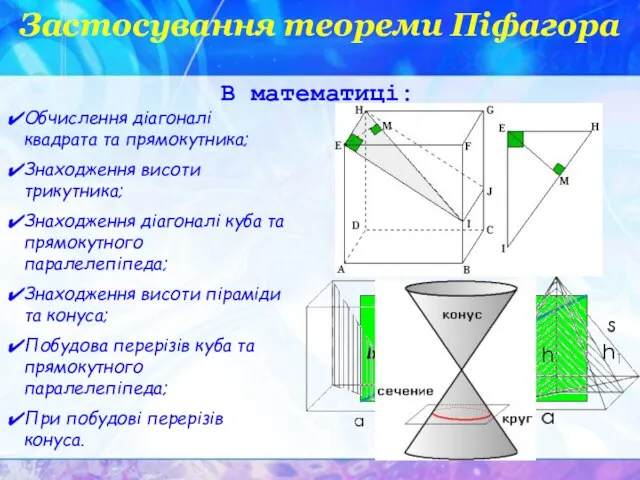
- 21. Застосування теореми Піфагора Обчислення діагоналі квадрата та прямокутника; Знаходження висоти трикутника; Знаходження діагоналі куба та прямокутного
- 22. Застосування теореми Піфагора В архітектурі При побудові будь-якої споруди розраховують відстані, центри тяжіння, розміщення опор, балок,
- 23. Застосування теореми Піфагора В астрономії При розрахунках шляху, який проходить промінь світла; Обчислення висоти антени мобільного
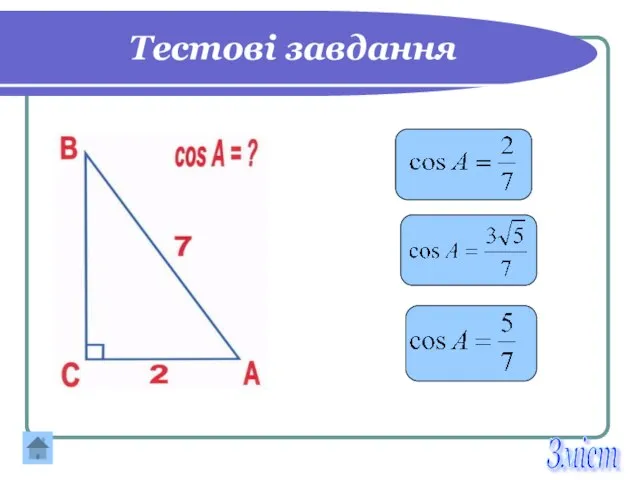
- 24. Тестові завдання Зміст
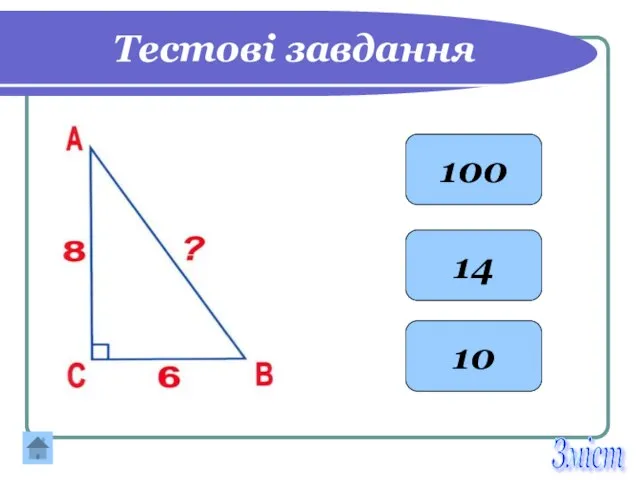
- 25. Тестові завдання 100 14 10 Зміст
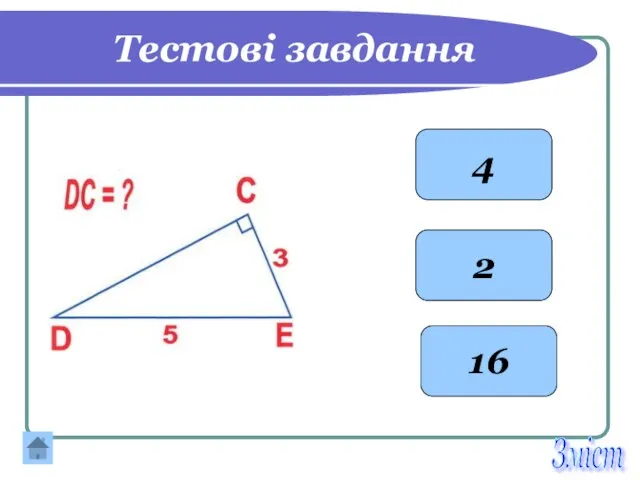
- 26. Тестові завдання 4 2 16 Зміст
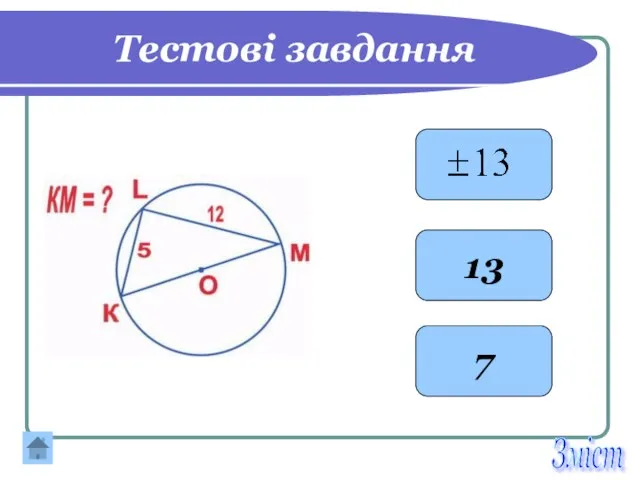
- 27. Тестові завдання 13 7 Зміст
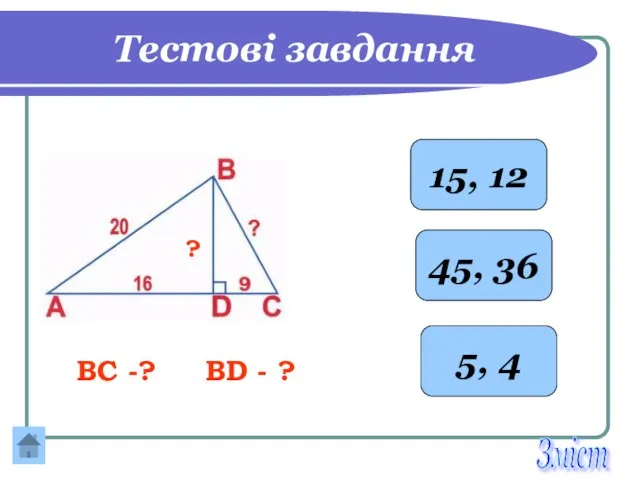
- 28. Тестові завдання 45, 36 5, 4 15, 12 ? ВС -? ВD - ? Зміст
- 29. Задача індійського математика XII століття Бхаскари «На березі річки росла тополя одинока. Зненацька вітра подих її
- 30. Задача з китайської «Математики в дев'яти книгах» У ставку, діаметр якого 1 чжан = 10 чи,
- 31. Задача з підручника «Арифметика» Леонтія Магницького Може трапитись пересічній людині до стіни драбину приладити, причому стіни
- 32. Задача про бамбук з давньокитайського трактату "Гоу-гу" Є бамбук завдовжки 1 чжан. Верхівку його зігнули таким
- 33. Молодець!
- 34. Помилка! Спробуй ще!
- 36. Скачать презентацию
























 Числовые последовательности. 9 класс
Числовые последовательности. 9 класс Объемы. Объем прямоугольного параллелепипеда
Объемы. Объем прямоугольного параллелепипеда Структура курсовой работы по дисциплине «Элементарная математика»
Структура курсовой работы по дисциплине «Элементарная математика» Меньше на некоторое число.
Меньше на некоторое число. Презентация по математике "Кубик рубика" - скачать
Презентация по математике "Кубик рубика" - скачать  Пересечение цилиндров
Пересечение цилиндров Автор работы: Перчикова Антонина Васильевна
Автор работы: Перчикова Антонина Васильевна  Сравнение отрезков и углов
Сравнение отрезков и углов Золотое сечение
Золотое сечение выполнила ученица 5а класса Пятакова Дарья
выполнила ученица 5а класса Пятакова Дарья Презентация по математике "Закрепление пройденного. Умножение и деление многозначных чисел" - скачать
Презентация по математике "Закрепление пройденного. Умножение и деление многозначных чисел" - скачать  Принятие решений при неполной информации. Классификация методов теории принятия решений
Принятие решений при неполной информации. Классификация методов теории принятия решений Основные понятия и аксиомы стереометрии
Основные понятия и аксиомы стереометрии Линейная алгебра. Лекция №1. Часть 1
Линейная алгебра. Лекция №1. Часть 1 Площадь круга
Площадь круга Взаимное расположение двух прямых, прямой и плоскости, двух плоскостей. (Лекция 4.1)
Взаимное расположение двух прямых, прямой и плоскости, двух плоскостей. (Лекция 4.1) Числа 1, 2, 3
Числа 1, 2, 3 Сравнение значений выражений
Сравнение значений выражений Неравенство треугольника
Неравенство треугольника Общее и различие в свойствах четырехугольников
Общее и различие в свойствах четырехугольников Теорема Пифагора
Теорема Пифагора Тестовые задания по математике для 9 класса
Тестовые задания по математике для 9 класса Взаимное расположение прямых и плоскосте в пространстве
Взаимное расположение прямых и плоскосте в пространстве Задачи городского тура олимпиады
Задачи городского тура олимпиады Математика в торговле
Математика в торговле Призма
Призма Презентация на тему Квадратный корень из степени
Презентация на тему Квадратный корень из степени  Десятичные дроби
Десятичные дроби