Содержание
- 2. Учебные пособия по курсу «Дискретная математика»:
- 3. П.С. Довгий, В.И. Поляков, В.И. Скорубский Основы теории множеств и приложение булевой алгебры к синтезу комбинационных
- 4. П.С. Довгий, В.И. Поляков СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ Учебное пособие к курсовой работе по дисциплине "Дискретная математика"
- 5. П.С. Довгий, В.И. Поляков АРИФМЕТИЧЕСКИЕ ОСНОВЫ ЭВМ Учебно-методическое пособие по выполнению домашних заданий по дисциплине "Дискретная
- 6. В.И. Поляков, В.И. Скорубский Математическая логика Учебное пособие по дисциплине «Математическая логика и теория алгоритмов» Санкт-Петербург
- 7. В.И. Поляков, В.И. Скорубский ОСНОВЫ ТЕОРИИ АЛГОРИТМОВ Учебное пособие по дисциплине «Математическая логика и теория алгоритмов»
- 8. Разделы курса «Дискретная математика»: Теория множеств - тест; Булева алгебра - тест; Синтез комбинационных схем –
- 9. Основные понятия теории множеств Отцом теории множеств считается Георг Кантор. Георг Кантор (1845 -1918) Ему принадлежит
- 10. Г. Кантору принадлежит следующая формулировка понятия множества: «Множество — это объединение определённых, различных объектов, называемых элементами
- 11. В основе теории множеств лежат первичные понятия: множество и отношение «быть элементом множества». Под множеством будем
- 12. Объекты, образующие некоторое множество, называются его элементами. Принадлежность некоторого элемента x множеству A обозначается как x∈A
- 13. Среди производных понятий теории множеств наиболее важны следующие: Пустое множество. Пустым множеством называется множество, не содержащее
- 14. Пустое множество является подмножеством любого множества. Универсальное множество. Обычно, в конкретных рассуждениях элементы всех множеств берутся
- 15. Мощность множества можно рассматривать как числовую характеристику (метрику) любого множества. Мощностью некоторого конечного множества А является
- 16. Конечные и бесконечные множества. Множества, имеющие конечное число эле-ментов и, соответственно, конечное значе-ние мощности, называются конечными,
- 17. Счетные и несчетные множества. Бесконечные множества разделяются на счётные и несчетные. Бесконечное множество называется счетным, если
- 18. В свою очередь, простейшим примером несчетного множества является множество действительных чисел. Другими примерами счетных множеств являются
- 19. Булеан множества. Любое конечное множество содержит и конечное число подмножеств. Связь между произвольным множеством и всеми
- 20. Булеан, как множество всех подмножеств множества А, должен включать в себя: пустое множество; само множество А;
- 21. Пример. Записать булеан (множество – степень) для множества А={a, b, c}. B(A)={∅, {a}, {b}, {c}, {a,
- 22. Способы задания множеств 1. Задание множеств списком предполагает перечисление элементов. Например, множество А состоит из букв
- 23. 3. Задание множества описанием свойств элементов. Например, M - это множество чисел, являющихся степенями двойки. К
- 24. Например: S - множество успевающих студентов. Разрешающей процедурой включения во множес-тво S является отсутствие неудовлетворительных оценок
- 25. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены.
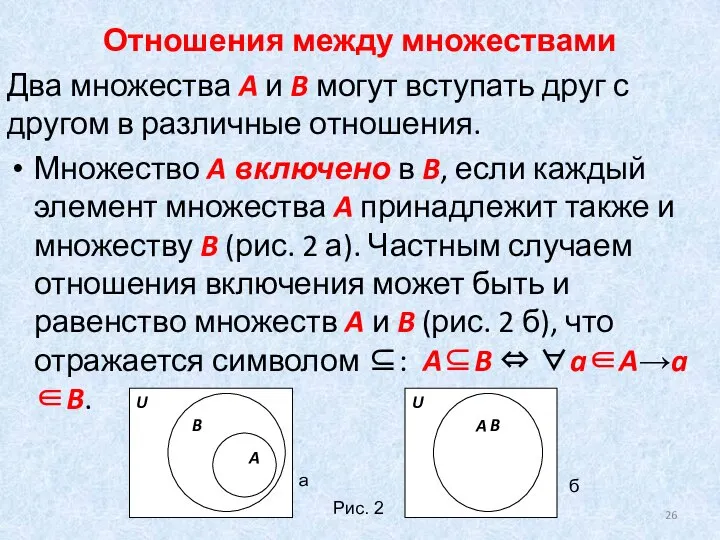
- 26. Отношения между множествами Два множества A и B могут вступать друг с другом в различные отношения.
- 27. Подобное отношение можно называть нестрогим включением. Довольно часто требуется исключить равенство множеств из отношения включения, в
- 28. Отношения между множествами могут обладать следующими свойствами: рефлексивностью, симметричностью и транзитивностью. Свойство рефлексивности является унарным, т.е.
- 29. Свойство симметричности является бинарным (двухместным), т.е. применимо к двум объектам. Отношение является симметричным, если оно выполняется
- 30. В свою очередь, отношение между двумя объек-тами не обладает свойством симметричности, т.е. является антисимметричным, если его
- 31. Свойство транзитивности является тернарным, т.е. применяется к трем объектам. Отношение R между объектами a, b, с
- 32. Отношение нестрогого включения обладает свойствами: рефлексивности: А ⊆ А; антисимметричности: (A ⊆ В и B ⊆
- 33. Для комбинации отношений строгого и нестрогого включений: (A ⊆ В и B ⊂ C) → (A
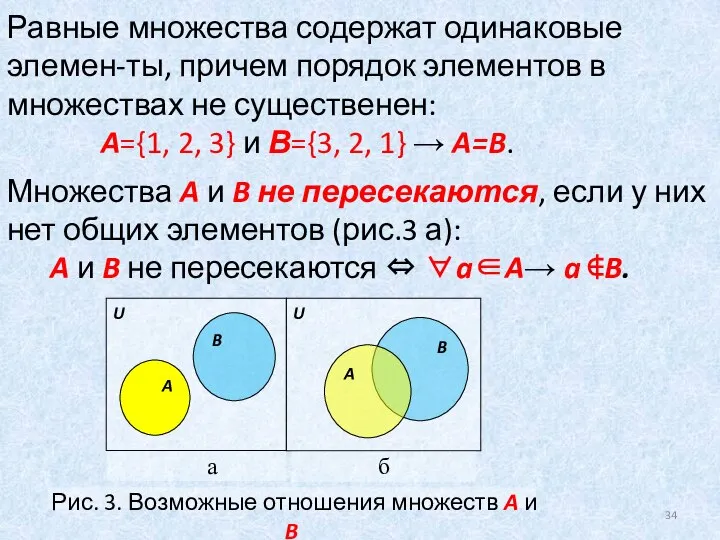
- 34. Равные множества содержат одинаковые элемен-ты, причем порядок элементов в множествах не существенен: A={1, 2, 3} и
- 35. Множества A и B находятся в общем положении, если существуют элемент, принадлежащий исклю-чительно множеству A, элемент,
- 36. Рассмотрим отношения между числовыми мно-жествами, для которых будем использовать следующие обозначения: S – множество простых чисел;
- 37. R– – множество неположительных действительных чисел; V – множество рациональных чисел; W – множество иррациональных чисел;
- 38. Алгебра множеств Множество всех подмножеств универсального множества U вместе с операциями над множест-вами образуют так называемую
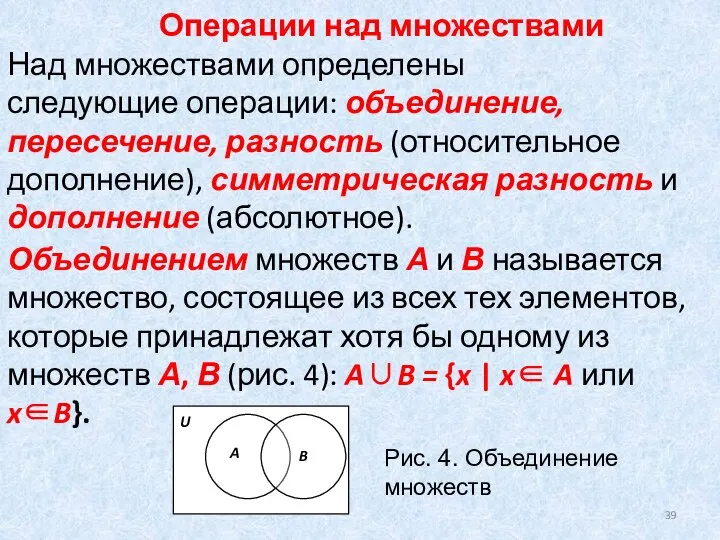
- 39. Операции над множествами Над множествами определены следующие операции: объединение, пересечение, разность (относительное дополнение), симметрическая разность и
- 40. Операцию объединения можно распространить на произвольное, в том числе и бесконечное количество множеств, например, М=А∪В∪С∪D. В
- 41. 2. , если S – бесконечная совокупность пронумерованных множеств; 3. , если набор индексов множеств задан
- 42. Рис. 5. Пересечение множеств Аналогично определяется пересечение произ-вольной (в том числе бесконечной) совокупности множеств. Обозначение для
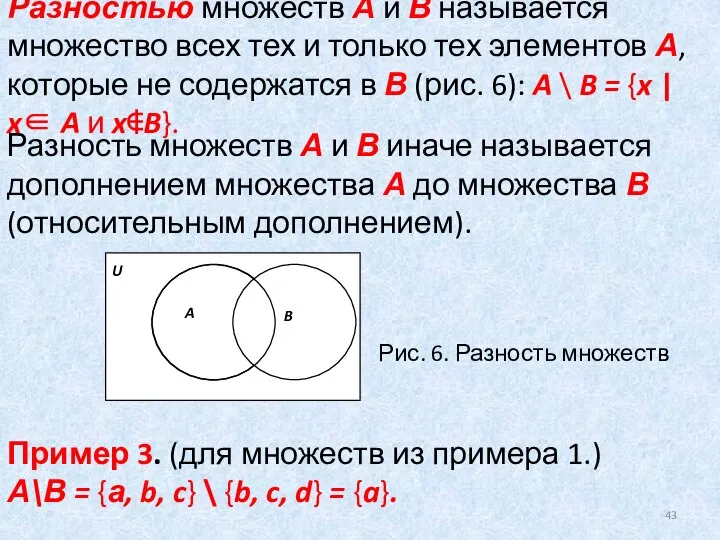
- 43. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не
- 44. Симметрической разностью множеств А и В называется множество, состоящее из элементов, которые принадлежат либо только множеству
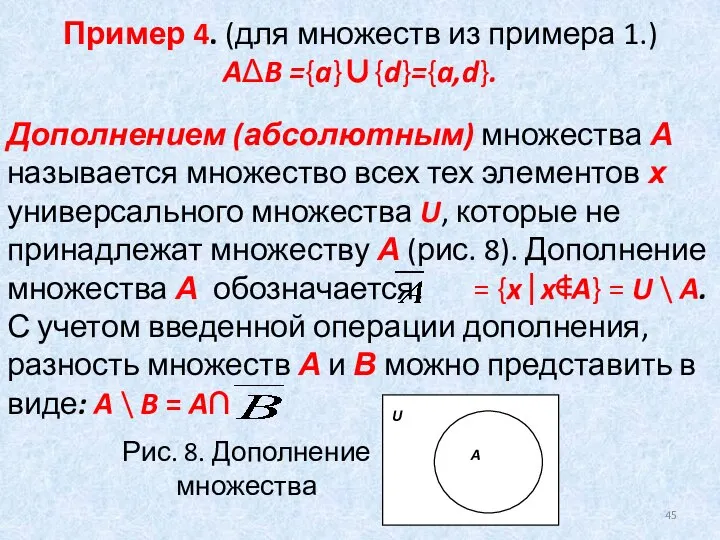
- 45. Пример 4. (для множеств из примера 1.) AΔB ={a}∪{d}={a,d}. Дополнением (абсолютным) множества А называется множество всех
- 46. Операции над множествами используются для получения новых множеств из уже существующих. Порядок выполнения операций над множествами
- 47. ∅. 4. Законы тавтологии (идемпотентности): A∪A= A; A∩A= A. 5. Законы двойственности (де Моргана): Следствия из
- 48. 15. Дополнительные тождества для операции симметрической разности: AΔ(BΔC) = (AΔB) ΔC; A∩(BΔC) = (A∩B) Δ(A∩C). Дополнительные
- 49. Способы доказательства тождеств Убедиться в справедливости тождеств можно с помощью диаграмм Эйлера-Венна. Для этого необходимо изобразить
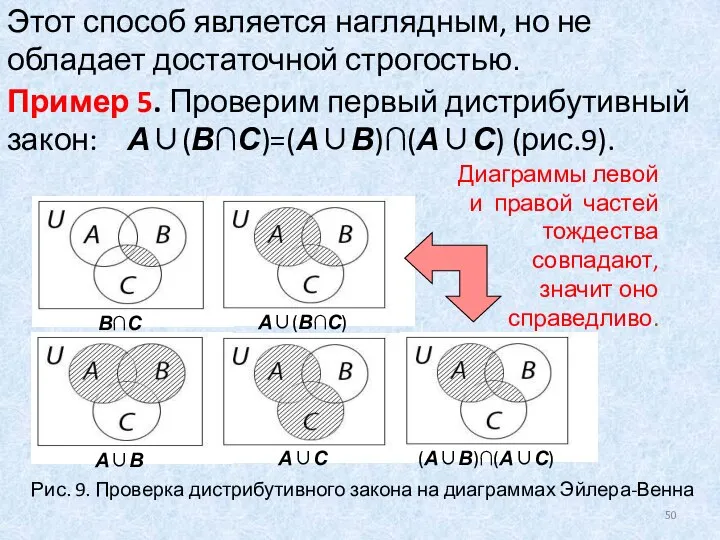
- 50. Пример 5. Проверим первый дистрибутивный закон: А∪(В∩С)=(А∪В)∩(А∪С) (рис.9). Диаграммы левой и правой частей тождества совпадают, значит
- 51. Доказательство справедливости проверяемых тождеств можно проводить одним из двух методов: - методом взаимного включения; - алгебраическим
- 52. В соответствии с принятым методом доказательство разделяется на две части: 1. Пусть элемент х∈ Dl, т.е.
- 53. б) Если элемент х∈В∩С, то, по определению операции пересечения множеств, (х∈В) и (х∈С), отсюда, по определению
- 54. 2. Пусть элемент х∈Dr, т.е. (х∈А∪В) и (х∈А∪С), откуда по определению операции объединения, (х∈А или х∈В)
- 55. 1. Пусть элемент x∈Dl , т.е. x∈ . Тогда x∈U и (x∉А∪В), значит x ∉ А
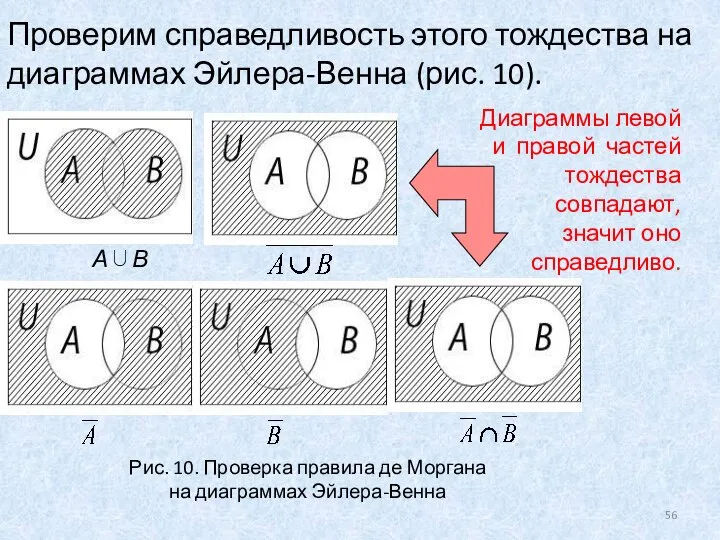
- 56. Проверим справедливость этого тождества на диаграммах Эйлера-Венна (рис. 10). Диаграммы левой и правой частей тождества совпадают,
- 57. А∩(А∪В) = ⇑ свойство пустого множества (А∪∅)∩(А∪В) = ⇑ по дистрибутивному закону (А∪(∅∩B)) = ⇑ свойство
- 58. Элементы, образующие вектор, называются координатами или компонентами вектора. Число координат вектора называется его длиной или размерностью.
- 59. Векторы длины два называются упорядоченными парами (или просто парами), длины три – тройками, …, длины n
- 60. В связи с этим множества, содержащие одинако-вые элементы, но в различном порядке, равны {a, b} =
- 61. Замечание. Из рассмотренного примера видно, что А×В ≠ В×А, т.е. коммутативный закон для прямого произведения множеств
- 62. Точка на плоскости может быть задана упорядо-ченной парой координат, т.е. двумя точками на координатных осях. Так
- 63. Пример 11. Х – множество точек отрезка [0;1]; Y – множество точек отрезка [1;2]; Z –
- 64. Тогда мощность их прямого произведения равна произведению мощностей множеств – сомножителей, т.е. ⏐А1×А2×…×Аn⏐=m1⋅m2 ⋅ … ⋅
- 66. Скачать презентацию






















































![Пример 11. Х – множество точек отрезка [0;1]; Y – множество](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1461456/slide-62.jpg)

 Лист Мёбиуса
Лист Мёбиуса Моделирование ситуаций. Виды моделей
Моделирование ситуаций. Виды моделей Отрезок. Лабораторно-практическая работа
Отрезок. Лабораторно-практическая работа Урок математики «Закрепление письменных приемов сложения и вычитания» Учитель: Циндяйкина С. А. 2 класс
Урок математики «Закрепление письменных приемов сложения и вычитания» Учитель: Циндяйкина С. А. 2 класс  Презентация по математике "Рациональные уравнения" - скачать бесплатно
Презентация по математике "Рациональные уравнения" - скачать бесплатно Меньше на некоторое число.
Меньше на некоторое число. Область определения выражения
Область определения выражения Вписанная и описанная окружность
Вписанная и описанная окружность Презентация на тему Наибольший общий делитель. Взаимно простые числа.
Презентация на тему Наибольший общий делитель. Взаимно простые числа. Метод математической индукции
Метод математической индукции Проверка статистических гипотез
Проверка статистических гипотез Разложение многочленов на множители с помощью комбинации различных приемов, решение уравнений. 7 класс
Разложение многочленов на множители с помощью комбинации различных приемов, решение уравнений. 7 класс Решение транспортной задачи. Составление опорного плана
Решение транспортной задачи. Составление опорного плана Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Статистические группировки
Статистические группировки Задачи С4. Как находить высоты и биссектрисы треугольника
Задачи С4. Как находить высоты и биссектрисы треугольника Логические задачи
Логические задачи Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Таблиця множення числа 3. Знаходження значень виразів на дії різних ступенів
Таблиця множення числа 3. Знаходження значень виразів на дії різних ступенів Решение неравенств
Решение неравенств Связь между автоматами Мили и Мура
Связь между автоматами Мили и Мура Кривые второго порядка
Кривые второго порядка Мінімізація скінченного автомата. (Тема 5)
Мінімізація скінченного автомата. (Тема 5) Проектирование разноритмичных и неритмичных потоков
Проектирование разноритмичных и неритмичных потоков МАТЕМАТИКА 1 КЛАСС
МАТЕМАТИКА 1 КЛАСС ЕГЭ 2016. Базовый уровень
ЕГЭ 2016. Базовый уровень Презентация по математике "Кабінет" - скачать
Презентация по математике "Кабінет" - скачать  Преобразования графика функции f(x)=x2
Преобразования графика функции f(x)=x2