Содержание
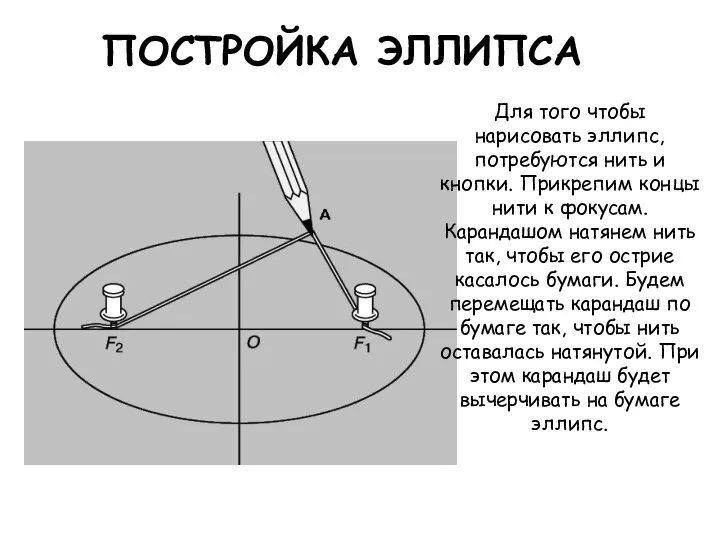
- 2. ПОСТРОЙКА ЭЛЛИПСА Для того чтобы нарисовать эллипс, потребуются нить и кнопки. Прикрепим концы нити к фокусам.
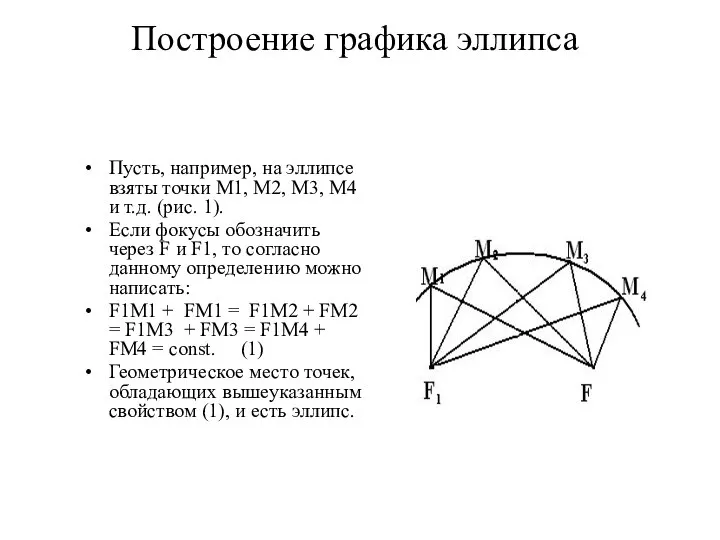
- 3. Построение графика эллипса Пусть, например, на эллипсе взяты точки M1, M2, M3, M4 и т.д. (рис.
- 4. 1. Эллипс и окружность ОПРЕДЕЛЕНИЕ. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до
- 5. уравнение эллипса. 3. Построим эллипс.
- 6. Уравнение (1): называется каноническим уравнением эллипса. Система координат, в которой эллипс имеет такое уравнение, называется его
- 7. СВОЙСТВА ЭЛЛИПСА 1) Эллипс лежит внутри прямоугольника, ограниченного x=±a, y=±b. 2) Эллипс имеет центр симметрии (начало
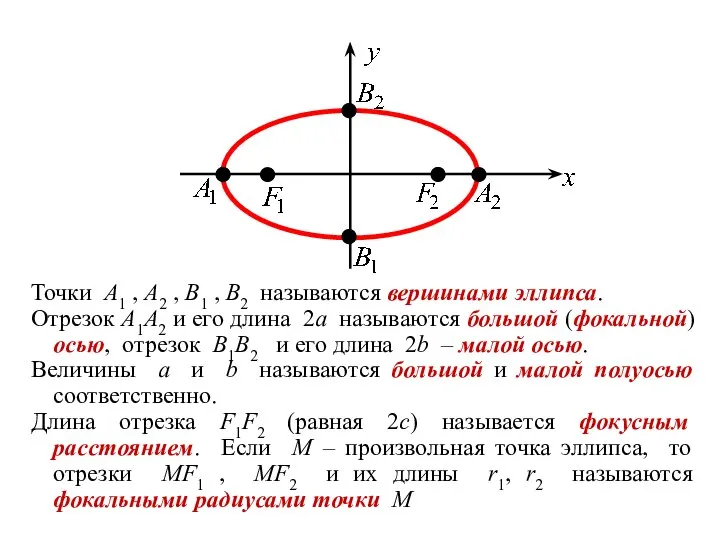
- 9. Точки A1 , A2 , B1 , B2 называются вершинами эллипса. Отрезок A1A2 и его длина
- 10. ОПРЕДЕЛЕНИЕ. Величина ε , равная отношению фокусного расстояния эллипса к его большой оси, называется эксцентриситетом эллипса,
- 11. 2) Если выбрать систему координат так, чтобы фокусы F1 и F2 были на оси Oy на
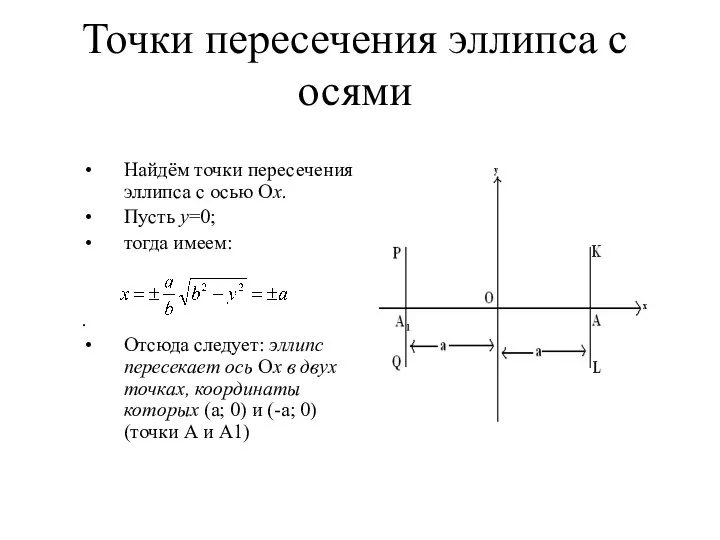
- 12. Точки пересечения эллипса с осями Найдём точки пересечения эллипса с осью Ох. Пусть у=0; тогда имеем:
- 13. Теоретический материал Окружность является частным случаем эллипса при Эксцентриситет окружности равен нулю. Чем ближе значение эксцентриситета
- 14. Теоретический материал Исследование формы эллипса по его уравнению Пример 1
- 15. Теоретический материал Пример 2
- 17. Скачать презентацию










 Упрощение выражений. 5 класс
Упрощение выражений. 5 класс Презентация по математике "Роль Франсуа Виета в математике" - скачать
Презентация по математике "Роль Франсуа Виета в математике" - скачать  Математика на войне
Математика на войне Схемы для решения задач на проценты
Схемы для решения задач на проценты Чёрный ящик. Источник множества интересных математических задач
Чёрный ящик. Источник множества интересных математических задач Арифметические диктанты
Арифметические диктанты Игровые модели. Классификация игр. Теория игр
Игровые модели. Классификация игр. Теория игр Способы решения квадратных уравнений
Способы решения квадратных уравнений Виды ДУ 1 порядка и методы их решения
Виды ДУ 1 порядка и методы их решения Геометрические преобразования
Геометрические преобразования Презентация для класса Числовой луч
Презентация для класса Числовой луч  Презентация по математике "КВН по математике в 3 классе" - скачать бесплатно
Презентация по математике "КВН по математике в 3 классе" - скачать бесплатно Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Дифференциальные уравнения
Дифференциальные уравнения Решение задач № 6 ЕГЭ
Решение задач № 6 ЕГЭ Практическое занятие к расчету ректификационной колонны бинарной смеси по х-у диаграмме
Практическое занятие к расчету ректификационной колонны бинарной смеси по х-у диаграмме Нелинейный осциллятор. Фазовый портрет
Нелинейный осциллятор. Фазовый портрет Первообразная функции. Неопределенный интеграл
Первообразная функции. Неопределенный интеграл Параллельность прямых в пространстве
Параллельность прямых в пространстве Использование тестирующей оболочки MyTestХ на уроках математики
Использование тестирующей оболочки MyTestХ на уроках математики Числа и точки на прямой. 5 класс
Числа и точки на прямой. 5 класс Первые уроки в 5 кассе
Первые уроки в 5 кассе Урок математики в 1 классе Учитель Устинова Б.А. Тема: Закрепление пройденного. Цели: I. Совершенствовать вычислительные навыки, ум
Урок математики в 1 классе Учитель Устинова Б.А. Тема: Закрепление пройденного. Цели: I. Совершенствовать вычислительные навыки, ум Сокращение алгебраических дробей. Алгебра 7 класс
Сокращение алгебраических дробей. Алгебра 7 класс Интерактивная игра. Волшебный счет (средняя группа)
Интерактивная игра. Волшебный счет (средняя группа) Задачи на кратное сравнение. Закрепление
Задачи на кратное сравнение. Закрепление Первообразная Тема Урока:
Первообразная Тема Урока:  Аттестационная работа. Образовательная программа внеурочной деятельности Юный математик
Аттестационная работа. Образовательная программа внеурочной деятельности Юный математик