Содержание
- 2. СЛУЧАЙНАЯ ВЕЛИЧИНА Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно
- 3. Таким образом, если каждому элементарному событию ω можно поставить в соответствие некоторое число, то говорят, что
- 4. ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА Случайная величина, принимающая значения, которые можно записать в виде конечного набора или счетной
- 5. ПРИМЕРЫ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН число дней в наугад взятом году (365, 366); число родившихся мальчиков среди
- 6. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА Случайная величина, которая может принимать все значения из некоторого числового промежутка, называется непрерывной
- 7. рост человека от 150 до 200 см; температура воздуха в случайно выбранный день; скорость самолета в
- 8. ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА Каждому значению хn дискретной случайной величины отвечает определенная вероятность pn.
- 9. ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СВ Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины
- 10. РЯД РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СВ Закон распределения дискретной случайной величины обычно задается в виде таблицы:
- 11. В верхней строке записывают возможные значения хi случайной величины X, а в нижней – их вероятности
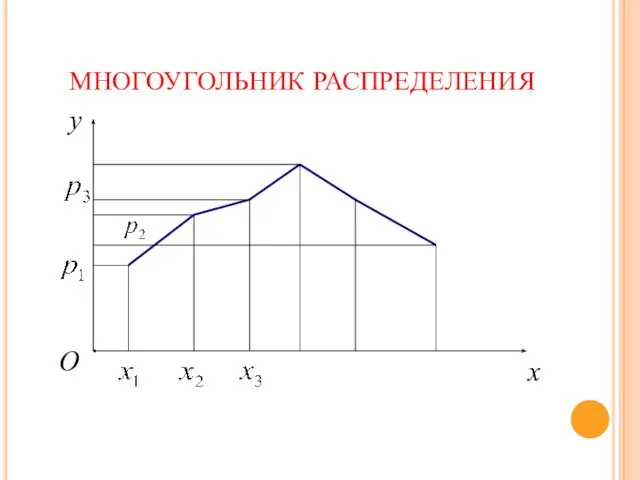
- 12. МНОГОУГОЛЬНИК РАСПРЕДЕЛЕНИЯ Для наглядности закон распределения дискретной случайной величины можно изобразить графически: построить точки (xi, pi)
- 13. МНОГОУГОЛЬНИК РАСПРЕДЕЛЕНИЯ x y O
- 14. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ Математическим ожиданием МХ=М(Х) дискретной случайной величины X называют сумму
- 15. ПРИМЕР Пример. Подбрасывается игральная кость. Найдите математическое ожидание дискретной случайной величины X, равной числу выпавших очков.
- 16. ЗАМЕЧАНИЕ Отметим, что постоянную величину C можно рассматривать как дискретную случайную величину, принимающую лишь одно значение
- 17. СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 1. Постоянный множитель можно выносить за знак математического ожидания, т.
- 18. ПРИМЕР Заработная плата имеет след. ряд распределения: Найти среднюю зарплату. Решение. Средняя заработная плата – это
- 19. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ Следует заметить, что математическое ожидание характеризует случайную величину не полностью. Зная математическое ожидание, нельзя
- 20. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ Бывает, что СВ с равными МХ могут существенно различаться по степени близости к нему
- 21. ДИСПЕРСИЯ Второй важной особенности СВ является разброс значений этой СВ по отношению к центру её распределения,
- 22. СВОЙСТВА ДИСПЕРСИИ Дисперсия – величина неотрицательная, т. е. D(X)≥0. Дисперсия постоянной равна нулю: D(X) =0. Постоянная
- 23. Пример. В предыдущем примере найдем D(X). Сначала найдём M(X2). Для этого построим ряд распределения СВ X
- 24. СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ Квадратный корень из дисперсии случайной величины X называется ее средним квадратическим отклонением и
- 25. Введение среднего квадратического отклонения объясняется тем, что дисперсия измеряется в квадратных единицах относительно размерности самой случайной
- 26. Дискретная случайная величина может быть задана законом распределения, представляющим собой перечень всех возможных значений этой случайной
- 27. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Функцией распределения вероятностей случайной величины X называют функцию F(x), определяющую вероятность
- 28. СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ЛЮБОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 0 ≤F(x) ≤ 1. Это свойство следует из того факта,
- 29. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Функция распределения дискретной случайной величины X имеет вид: где суммируются вероятности
- 30. ПРИМЕР. ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ X ЗАДАН ТАБЛИЦЕЙ: Найдите функцию распределения случайной величины X Решение.
- 31. ПРИМЕР Таким образом, получаем функцию распределения вида:
- 32. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Случайная величина X называется непрерывной, если существует функция p(x) такая,
- 33. ТЕОРЕМА Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее полуинтервалу [a,b) равна определенному интегралу
- 34. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку
- 35. Дисперсией непрерывной случайной величины X называют математическое ожидание квадрата ее отклонения. Если возможные значения Х принадлежат
- 37. Скачать презентацию

































 Линейные уравнения Выполнила ученица 7 класса МОУ «Янгильдинская СОШ» Калишова Ирина
Линейные уравнения Выполнила ученица 7 класса МОУ «Янгильдинская СОШ» Калишова Ирина Кто сигару поджигает - Жизнь на годы сокращает, Окружающим, себе, Может быть, тебе и мне.
Кто сигару поджигает - Жизнь на годы сокращает, Окружающим, себе, Может быть, тебе и мне. Решение иррациональных уравнений
Решение иррациональных уравнений В науке о числах… надо ожидать весьма В науке о числах… надо ожидать весьма
В науке о числах… надо ожидать весьма В науке о числах… надо ожидать весьма  Семь вопросов по планиметрии
Семь вопросов по планиметрии Презентация по математике "Арифметическая и геометрическая прогрессии" - скачать
Презентация по математике "Арифметическая и геометрическая прогрессии" - скачать  Сложение и вычитание десятичных дробей. Витамины
Сложение и вычитание десятичных дробей. Витамины Сравнение десятичных дробей
Сравнение десятичных дробей Задача о кратчайшем пути
Задача о кратчайшем пути Элективный курс. Алгебра 11 класс. Уроки 09
Элективный курс. Алгебра 11 класс. Уроки 09 Элементы теории вероятности. Противоположные события. Их вероятность. 9 класс (2)
Элементы теории вероятности. Противоположные события. Их вероятность. 9 класс (2) Сумма n-первых членов арифметической прогрессии
Сумма n-первых членов арифметической прогрессии Площадь поверхности
Площадь поверхности Четырехугольники. Прямоугольник. Ромб. Квадрат
Четырехугольники. Прямоугольник. Ромб. Квадрат Общие сведения о науке - внешняя баллистика ракет
Общие сведения о науке - внешняя баллистика ракет Показательные уравнения
Показательные уравнения Взаимно обратные числа
Взаимно обратные числа У Р А В Н Е Н И Е Урок математики, 5 класс. Учитель математики: Ожеред Сергей Тимофеевич МОУ-СОШ с.Батурино Асиновского р-на
У Р А В Н Е Н И Е Урок математики, 5 класс. Учитель математики: Ожеред Сергей Тимофеевич МОУ-СОШ с.Батурино Асиновского р-на  Векторы 9 класс
Векторы 9 класс Математика в обществознании Интегрированный урок-турнир в 10 классе
Математика в обществознании Интегрированный урок-турнир в 10 классе Космическое путешествие. Математика 6 класс
Космическое путешествие. Математика 6 класс Совместные действия с обыкновенными и десятичными дробями
Совместные действия с обыкновенными и десятичными дробями Умножение десятичных дробей. Устный счёт
Умножение десятичных дробей. Устный счёт Системы случайных величин
Системы случайных величин Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Признаки делимости
Признаки делимости Параллельные прямые в пространстве. (10 класс)
Параллельные прямые в пространстве. (10 класс) Алгоритм решения уравнений
Алгоритм решения уравнений