1.3. Вычисление двойного интеграла
Сведение двойного интеграла к двукратному. Продолжение
Аналогично, рассекая
тело Т плоскостями y = const ( c ≤ y ≤ d), площадь S(y) любого сечения, перпендикулярного к оси Оу определяется
Тогда
(Б)
В формуле (А) интегрирование выполняется вначале по у – в пределах при постоянном, но произвольном значении х, а затем по х – в пределах от x1=a до x2=b. В (Б) интегрирование выполняется: внутренний интеграл берется по х (при фиксированном у), пределы интегрирования указывают границы изменения х, в общем случае зависящие от у; внешний интеграл берется по у, пределы интегрирования постоянны и указывают границы изменения переменной.
Если область интегрирования D является правильной в направлении оси Оу и в направлении оси Ох, то вычисление двойного интеграла можно производить по (А) или по (Б).
Если нижняя или верхняя (левая или правая) линии границы области D представлены различными выражениями, область следует разбить прямыми, параллельными Оу (или Ох). Затем воспользоваться свойством аддитивности двойного интеграла.
Верхняя граница имеет уравнение дуги:
Инт. представить в виде суммы двух интегралов по областям
D1 и D2 (каждый по (А)):














 Таблицы. Геометрия
Таблицы. Геометрия Свойства логарифмов. Джон Непер (1550-1617)
Свойства логарифмов. Джон Непер (1550-1617) Решение задач
Решение задач Презентация на тему Параллелепипед
Презентация на тему Параллелепипед  Логическое высказывание. Виды сложных высказываний
Логическое высказывание. Виды сложных высказываний Математика в профессии “Технолог общественного питания”
Математика в профессии “Технолог общественного питания” Путешествие в мир обыкновенных
Путешествие в мир обыкновенных Рабочая программа по математике для 5 - 6 классов
Рабочая программа по математике для 5 - 6 классов Урок математики 3 класс
Урок математики 3 класс  График линейной функции
График линейной функции Устная работа. Вычисления
Устная работа. Вычисления Минутка занимательной математики
Минутка занимательной математики Прямая и отрезок. Луч и угол
Прямая и отрезок. Луч и угол Урок 11 Расстояния между прямыми
Урок 11 Расстояния между прямыми  Презентация на тему Векторы в пространстве
Презентация на тему Векторы в пространстве  Признаки делимости на 2, 5, 10 (часть 2)
Признаки делимости на 2, 5, 10 (часть 2) Матрицы и определители
Матрицы и определители Леонард Эйлер
Леонард Эйлер Рациональные дроби и их свойства
Рациональные дроби и их свойства Решение задач на построение. Трудность использования настоящего циркуля при изображении окружностей на доске
Решение задач на построение. Трудность использования настоящего циркуля при изображении окружностей на доске Таблицы частот
Таблицы частот Классификация треугольников
Классификация треугольников Logical expressions
Logical expressions Комбинаторика. Принципы комбинаторики. (Лекция 10)
Комбинаторика. Принципы комбинаторики. (Лекция 10)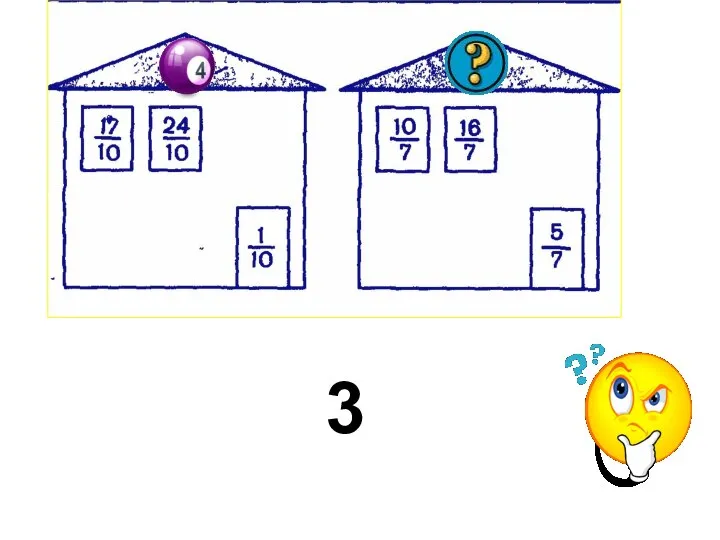 Задания по математике (5 класс, часть 5)
Задания по математике (5 класс, часть 5) Принцип Дирихле. 6 класс
Принцип Дирихле. 6 класс Электронно-образовательные ресурсы к учебнику математики 3 класса, часть 2 (автор Н. Б. Истомина) для фронтальной работы с интер
Электронно-образовательные ресурсы к учебнику математики 3 класса, часть 2 (автор Н. Б. Истомина) для фронтальной работы с интер Первообразная
Первообразная