Содержание
- 2. 5.1. Основные понятия
- 3. Ряд классических задач теории графов сводится к отысканию частей графа, экстремальных относительно некоторого свойства. Речь может
- 4. Максимальность и наибольшесть Определение. Наибольшей (наименьшей) частью графа по некоторому свойству называется макси-мальная (минимальная) часть с
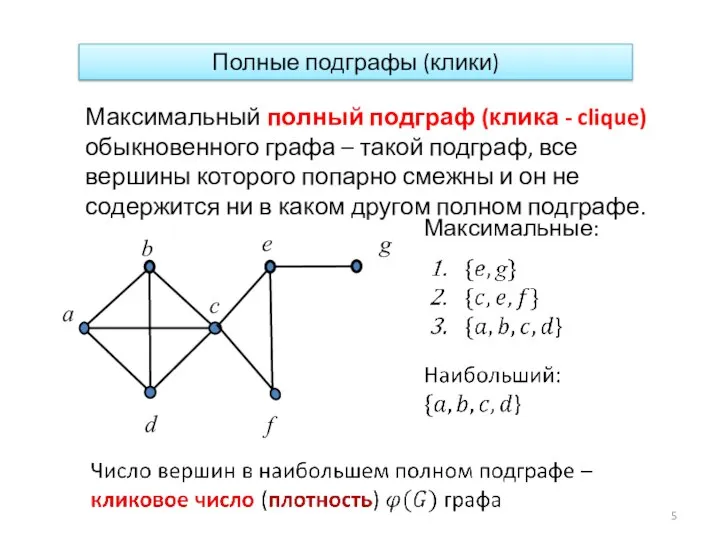
- 5. Полные подграфы (клики) Максимальный полный подграф (клика - clique) обыкновенного графа – такой подграф, все вершины
- 6. Пустые подграфы (ВУМ) Максимальный пустой подграф (независимое множество, внутренне устойчивое множество) – такой подграф, все вершины
- 7. Покрытия (доминирующие множества) Из доминирующего множества «видны» все вершины графа. Иначе оно называется вершинно – вершинным
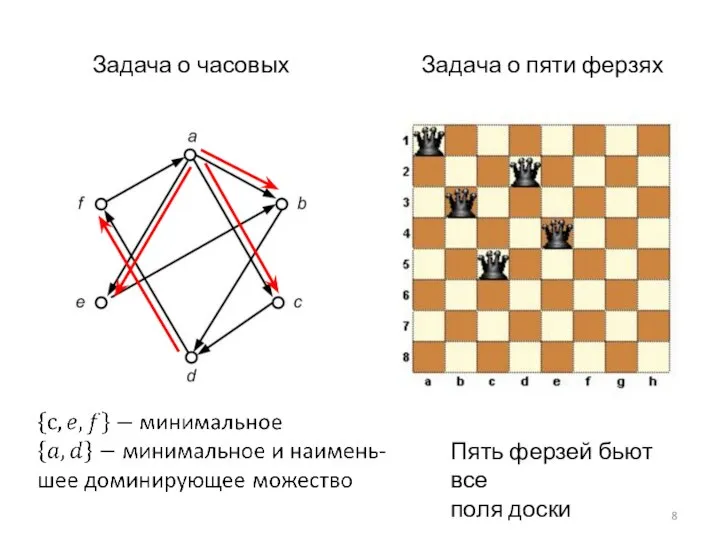
- 8. Задача о пяти ферзях Задача о часовых Пять ферзей бьют все поля доски
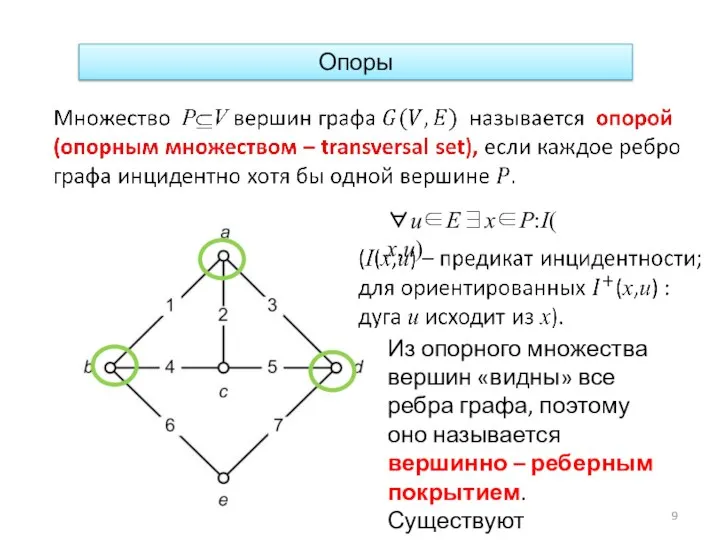
- 9. Опоры Из опорного множества вершин «видны» все ребра графа, поэтому оно называется вершинно – реберным покрытием.
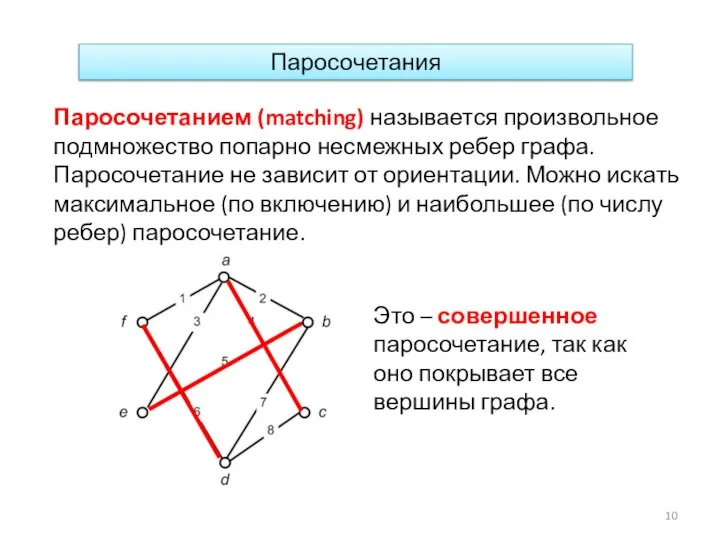
- 10. Паросочетания Паросочетанием (matching) называется произвольное подмножество попарно несмежных ребер графа. Паросочетание не зависит от ориентации. Можно
- 11. Взвешенные графы Многие прикладные задачи сводятся к проблеме нахождения экстремальных частей во взвешенных графах. Требуется найти
- 12. 5.2. Взаимосвязи между задачами нахождения экстремальных частей
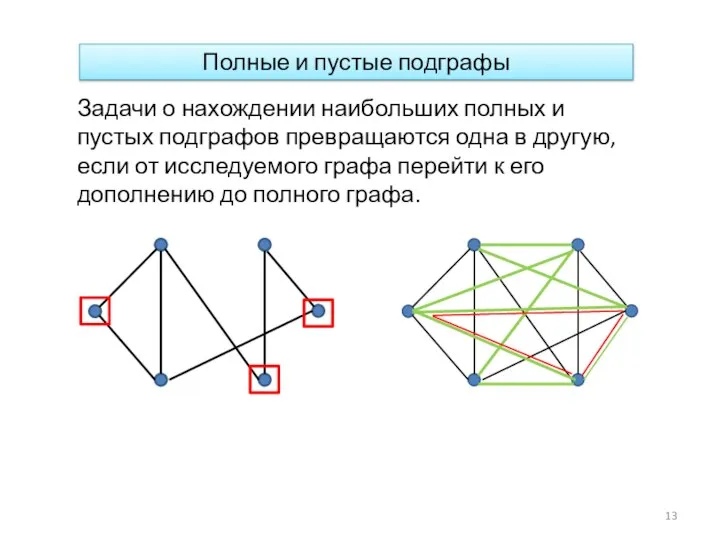
- 13. Задачи о нахождении наибольших полных и пустых подграфов превращаются одна в другую, если от исследуемого графа
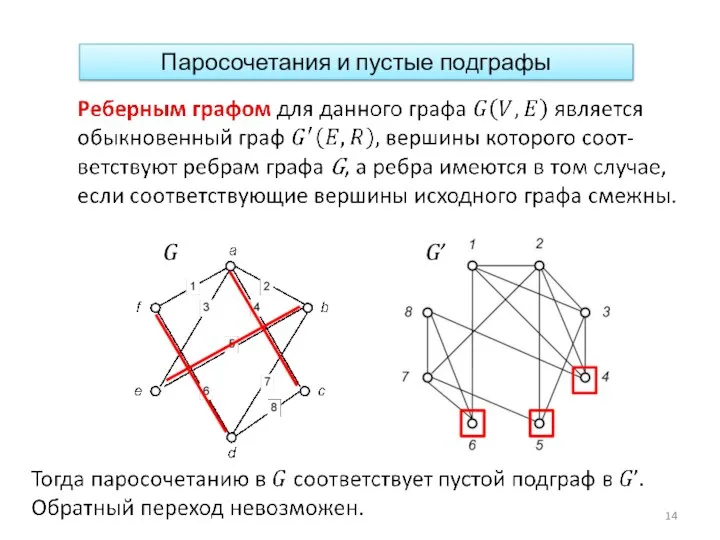
- 14. Паросочетания и пустые подграфы G G’
- 15. Опоры и пустые подграфы
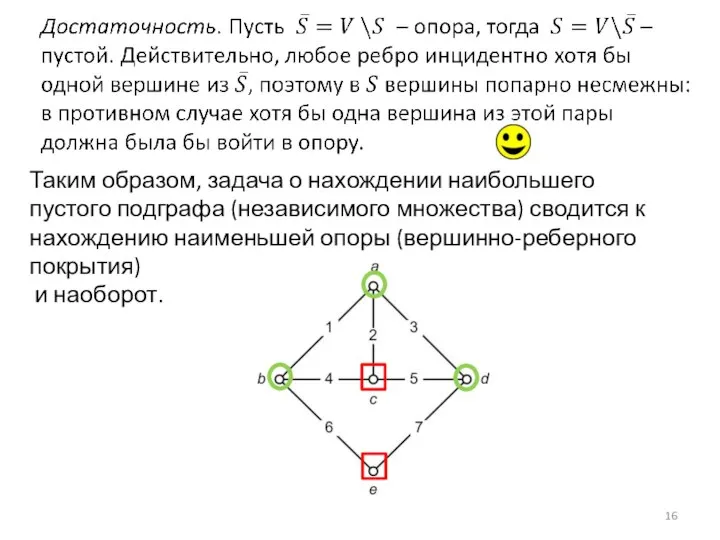
- 16. Таким образом, задача о нахождении наибольшего пустого подграфа (независимого множества) сводится к нахождению наименьшей опоры (вершинно-реберного
- 17. 5.3. Задача о наименьшем покрытии
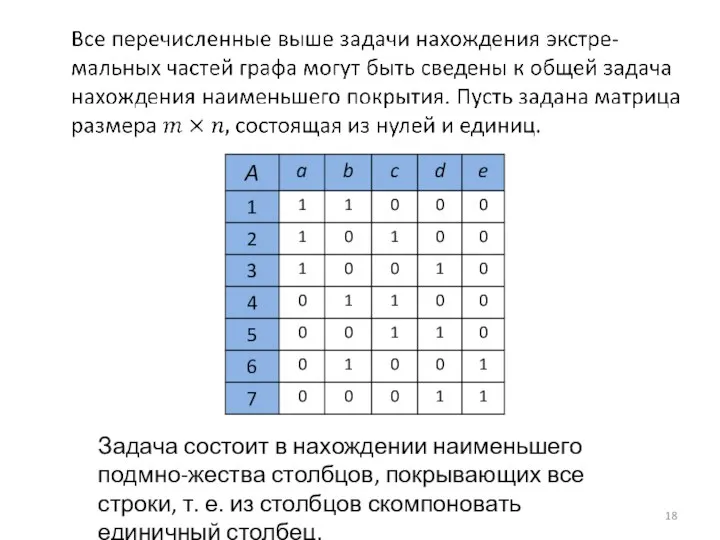
- 18. Задача состоит в нахождении наименьшего подмно-жества столбцов, покрывающих все строки, т. е. из столбцов скомпоновать единичный
- 19. Задача о наименьшем покрытии формулируется на матрице общего вида. Применительно к графам она может быть поставлена
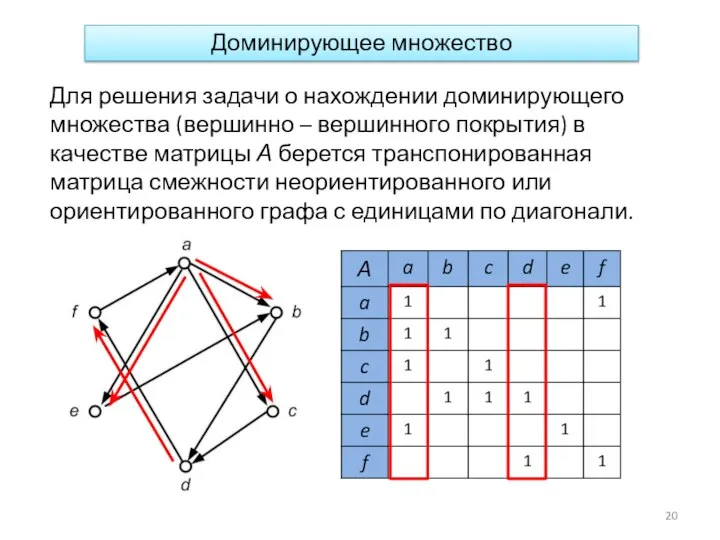
- 20. Доминирующее множество Для решения задачи о нахождении доминирующего множества (вершинно – вершинного покрытия) в качестве матрицы
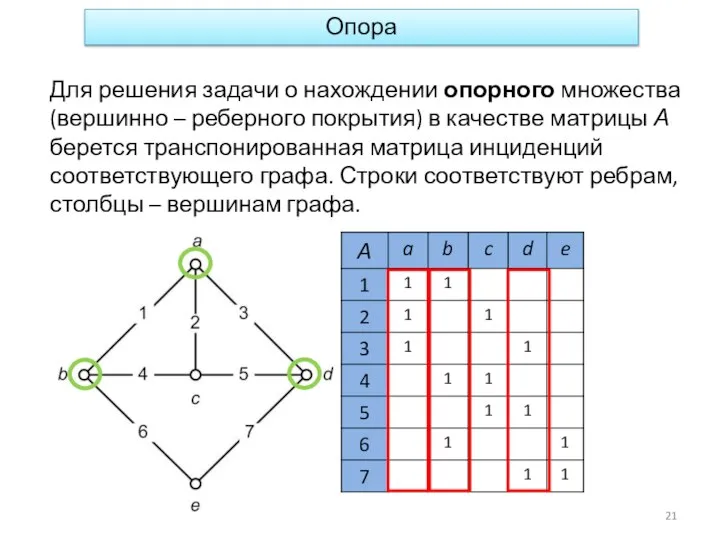
- 21. Опора Для решения задачи о нахождении опорного множества (вершинно – реберного покрытия) в качестве матрицы А
- 23. Скачать презентацию










 Круги, окружности и шары вокруг нас. 6 класс
Круги, окружности и шары вокруг нас. 6 класс Презентация на тему Викторина Математика – царица наук
Презентация на тему Викторина Математика – царица наук  Угол. Прямой и развернутый угол. Чертежный треугольник
Угол. Прямой и развернутый угол. Чертежный треугольник Solução Numérica de Equações Diferenciais
Solução Numérica de Equações Diferenciais УСТНЫЙ СЧЕТ 6 класс
УСТНЫЙ СЧЕТ 6 класс  Основные понятия и теоремы теории вероятностей. Тема 2. Часть 2
Основные понятия и теоремы теории вероятностей. Тема 2. Часть 2 Презентация на тему Сумма углов треугольника Решение задач
Презентация на тему Сумма углов треугольника Решение задач 5 класс
5 класс Урок математики в 6 классе. Тема: « Действия с положительными и отрицательными числами»
Урок математики в 6 классе. Тема: « Действия с положительными и отрицательными числами» Кригинг
Кригинг Решение задач
Решение задач Угол между прямой и плоскостью
Угол между прямой и плоскостью Умножение десятичных дробей Урок математики в 5 классе по теме:
Умножение десятичных дробей Урок математики в 5 классе по теме:  Задачи на построение угла. Биссектриса
Задачи на построение угла. Биссектриса Пересечение плоскостей
Пересечение плоскостей Графики
Графики Презентация по математике "Измерение отрезков" - скачать бесплатно
Презентация по математике "Измерение отрезков" - скачать бесплатно Презентацию подготовила Кулагина В.В. Учитель начальных классов ФКОУ СОШ имени А.Н.Радищева Г. Кузнецк-12 2012г.
Презентацию подготовила Кулагина В.В. Учитель начальных классов ФКОУ СОШ имени А.Н.Радищева Г. Кузнецк-12 2012г.  Десятичные дроби. Сложение и вычитание десятичных дробей
Десятичные дроби. Сложение и вычитание десятичных дробей Пропорции и отношения. Урок – игра «Математическая поликлиника» 6 класс
Пропорции и отношения. Урок – игра «Математическая поликлиника» 6 класс Решение задач на смеси и растворы с помощью уравнений
Решение задач на смеси и растворы с помощью уравнений Игры (геометрия). Статические игры
Игры (геометрия). Статические игры Развёртка прямоугольного параллелепипеда. Урок 143
Развёртка прямоугольного параллелепипеда. Урок 143 Математика. (2 класс)
Математика. (2 класс) Презентация на тему Экскурсия по Московскому кремлю
Презентация на тему Экскурсия по Московскому кремлю  Равносильные уравнения
Равносильные уравнения Коллекция картинок для уроков математики Часть 1
Коллекция картинок для уроков математики Часть 1 Интерактивная раскраска по математике. Сложение и вычитание круглых десятков
Интерактивная раскраска по математике. Сложение и вычитание круглых десятков