Элементы аналитической геометрии на плоскости

алгебры на основе метода координат и введения произвольной (переменной) точки объекта в Декартовой системе координат.
§1. ЛИНИИ НА ПЛОСКОСТИ
Прямая
Определение. Выражение F(x, y) = 0 называется уравнением данной линии, если ему удовлетворяют все точки, лежащие на данной линии и не удовлетворяет ни одна точка, не принадлежащая данной линии.
Всем известный «школьный» вид уравнения прямой, который называется уравнением прямой с угловым коэффициентом.
y=kx+b
Например, если прямая задана уравнением y=2x-2, то её угловой коэффициент: k=2.
Рассмотрим геометрический смысл данного коэффициента и то,  как его значение влияет на расположение прямой:

чем меньше угловой коэффициент по модулю, тем прямая является более пологой.

Если k>0, прямая идет снизу вверх, если k<0 – сверху вниз.

Чем больше b, тем выше пересекает прямая ось 0Y

Как составить уравнение прямой с угловым коэффициентом?
Если известна точка M(x0,y0), принадлежащая некоторой прямой, и угловой коэффициент k этой прямой, то уравнение данной прямой выражается формулой: y-y0=k(x-x0)

общим уравнением прямой на плоскости, где  A,B,C – некоторые числа. При этом коэффициенты A,B одновременно не равны нулю, так как уравнение теряет смысл.
Направляющий вектор прямой
Вектор, который параллелен прямой, называется направляющим вектором данной прямой.
Очевидно, что у любой прямой бесконечно много направляющих векторов, причём все они будут коллинеарны (сонаправлены или нет – не важно).
Направляющий вектор будем обозначать : 
Но одного вектора недостаточно для построения прямой, вектор является свободным и не привязан к какой-либо точке плоскости.
Поэтому дополнительно необходимо знать некоторую точку M(x0,y0), которая принадлежит прямой.

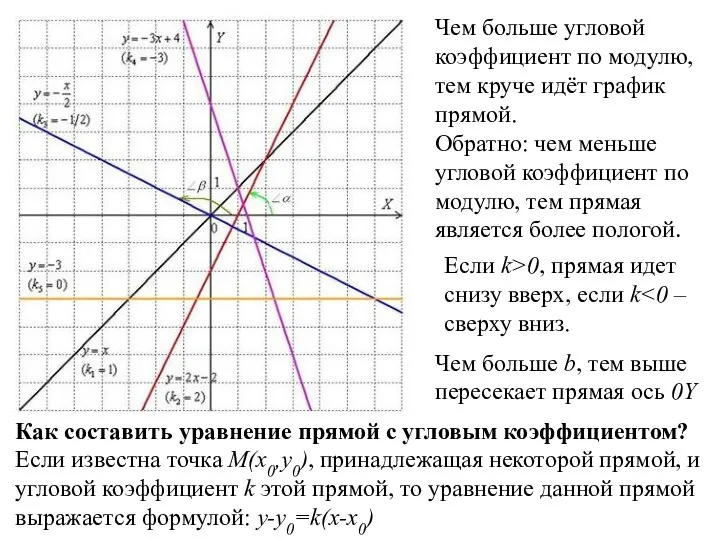
A=k
B=-1
C=b

1. Составить уравнение прямой по точке  M(1,2) и направляющему вектору p= (2,1)
Подставим координаты направляющего вектора p(2,1) и точки M(1,2) в уравнение

Чертежа в таких примерах, как правило, делать не нужно, но в качестве пояснения:

уравнением  Ax+By+C=0 в прямоугольной системе координат, то вектор  p(-B,C) является направляющим вектором данной прямой.
Примеры нахождения направляющих векторов прямых:
В том случае, если одна из координат направляющего вектора нулевая:
Как составить уравнение прямой по двум точкам?
Если известны две точки M1(x1,y1) и M2(x2,y2), то уравнение прямой, проходящей через данные точки, можно составить по формуле:

Поскольку вектор будет направляющим вектором данной прямой. 

уравнение прямой, проходящей через две заданные точки: M1(-2,-1), M2(3,1)
Решение:
Подставим координаты точек  M1(-2,-1), M2(3,1) в уравнение прямой.
Необходима проверка – координаты исходных точек должны удовлетворять полученному уравнению:
Задача решена верно.
Если в результате проверки тождества не получилось – надо все пересчитать.

обращается в ноль, то переписываем её в виде . 
Вектор нормали прямой (нормальный вектор)
Если прямая задана общим уравнением   Ax+By+C=0 в прямоугольной системе координат, то вектор n(A,B) является вектором нормали данной прямой.
Вектор нормали n(A,B) всегда ортогонален направляющему вектору прямой p(-B,C). Убедимся в ортогональности данных векторов с помощью скалярного произведения:
Приведем примеры с теми же уравнениями, что и для направляющего вектора:

прямой, то уравнение данной прямой выражается формулой:
Пример 3. Составить уравнение прямой по точке  M(-1,-3) и вектору нормали n(3,-1). Найти направляющий вектор прямой.
Решение. Используем формулу.

Выполним проверку: Вектор нормали n(3,-1) совпадает с коэффициентами A, B.
Точка M(-1,-3) лежит на прямой.

Уравнение составлено правильно. Вытаскиваем направляющий вектор прямой: