Содержание
- 2. Финансовый университет при Правительстве Российской Федерации Шевелёв Александр Юрьевич доцент, кандидат физико- математических наук.
- 3. Финансовый университет при Правительстве Российской Федерации Математика
- 4. Финансовый университет при Правительстве Российской Федерации Тема №13. Элементы математической статистики
- 5. Математическая статистика Предметом математической статистики является изучение совокупности однородных объектов относительно некоторого количественного или качественного признака,
- 6. Математическая статистика Наблюдения могут заключаться либо в измерении какого-нибудь параметра исследуемого объекта, либо в регистрации у
- 7. Математическая статистика К числу наиболее часто встречающихся задач математической статистики относятся: 1. Определение по результатам независимых
- 8. Математическая статистика 4. Проверка статистических гипотез о виде закона распределения или его числовых характеристиках; 5. Оценка
- 9. Математическая статистика В практике статистических наблюдений различают два вида: сплошное, когда изучаются все объекты и выборочное,
- 10. Генеральной совокупностью называют множество всех объектов над которыми необходимо произвести наблюдение. Выборочной совокупностью (выборкой) называется та
- 11. Число объектов в совокупности называется её объёмом. N – объём генеральной совокупности, n – объём выборки.
- 12. Математическая статистика Чтобы по выборке можно было уверенно судить об изучаемой случайной величине выборка должна быть
- 13. Математическая статистика При этом возможны два способа образования выборки: повторная и бесповторная. Повторной называют выборку, при
- 14. Математическая статистика Накопленные в процессе исследования или эксперимента данные сначала подвергают сортировке: ранжируют (упорядочение в порядке
- 15. Различные возможные значения случайной величины, соответствующие отдельной группе сгруппированного ряда наблюдаемых данных называются вариантами. Численность отдельной
- 16. Математическая статистика Частоты и доли вариантов обобщённо называются весами. Сумма частот равна объёму совокупности, а сумма
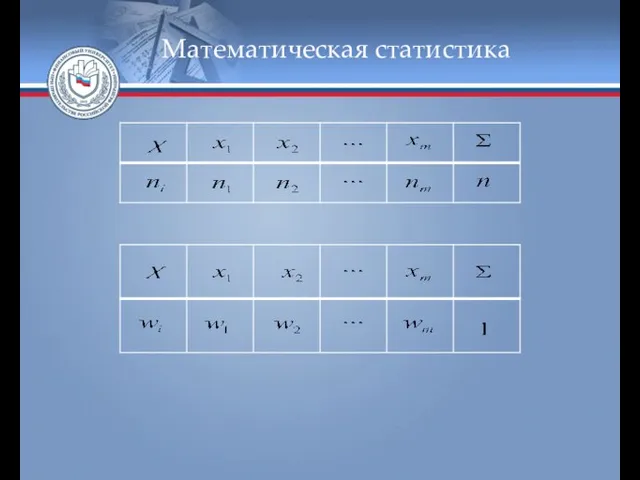
- 17. Ранжированный в порядке возрастания (или убывания) ряд вариантов с соответствующими им весами называется дискретным вариационным рядом.
- 18. Математическая статистика
- 19. Математическая статистика Если изучаемая случайная величина является непрерывной, то строится интервальный вариационный ряд. Длины интервалов называются
- 20. Математическая статистика Для наглядности интервальный вариационный ряд можно изобразить в прямоугольной системе координат в виде гистограммы,
- 21. Математическая статистика Полигоном частот или относительных частот называется ломаная линия, соединяющая точки с координатами
- 22. Математическая статистика Основными числовыми характеристиками вариационных рядов являются средняя арифметическая и дисперсия вариационного ряда. Средней арифметической
- 23. Математическая статистика По определению вести расчёты средней арифметической и дисперсии вариационного ряда бывает сложно. Можно пользоваться
- 24. Математическая статистика
- 25. Математическая статистика Известно, что для описания случайной величины достаточно знать её числовые характеристики (параметры). Например, математическое
- 26. Выборочная числовая характеристика t, используемая в качестве приближённого значения неизвестной числовой характеристики генеральной совокупности t, называется
- 27. Математическая статистика Средние арифметические, дисперсии, а также с.к.о. распределения признака в генеральной и выборочной совокупностях называются
- 28. Математическая статистика Выборочная средняя и выборочная доля являются точечными оценками генеральной средней и генеральной доли. Но
- 29. Интервальной оценкой параметра t называется числовой интервал (a; b), который с заданной доверительной вероятностью «накрывает» неизвестное
- 30. Доверительной вероятностью (надёжностью) называется вероятность того, что оценка x отклонится от оцениваемого параметра t по абсолютной
- 31. Наибольшее отклонение выборочной числовой характеристики от соответствующей ей генеральной характеристики, которое возможно с заданной доверительной вероятностью
- 32. Математическая статистика - Функция Лапласа, значения которой находятся в таблице. - выборочная средняя или доля, -
- 33. Среднее квадратическое отклонение оценки х параметра t собственно случайной выборки называется средней квадратической ошибкой выборки. Из
- 34. Математическая статистика Формулы для средних квадратических ошибок имеют вид:
- 35. Математическая статистика При интервальном оценивании решаются следующие задачи: Определение доверительного интервала при заданной доверительной вероятности и
- 36. Математическая статистика Формулы расчёта объёма выборки имеют вид:
- 37. Математическая статистика При оценке генеральной доли в отсутствии предварительных сведений о значениях дисперсии и доли нет,
- 38. Математическая статистика В науке и на практике часто ставится задача нахождения неизвестного закона распределения признака, являющегося
- 39. Математическая статистика Т.е. выдвигается статистическая гипотеза (предположение о виде или параметрах неизвестного закона распределения). Необходимо выяснить,
- 40. Математическая статистика Если на основании теоретических предпосылок и анализа опытных данных приходим к выводу, что изучаемый
- 41. Математическая статистика Затем вычисляют теоретические частоты, соответствующие опытным частотам по формуле: - интервальная разность - функция
- 42. Математическая статистика После этого выясняется степень согласованности данных эксперимента и статистической гипотезы. Для ответа на этот
- 43. Математическая статистика Полученное значение сравниваем с критическим (табличным). Для критического значения определяются число степеней свободы, которое
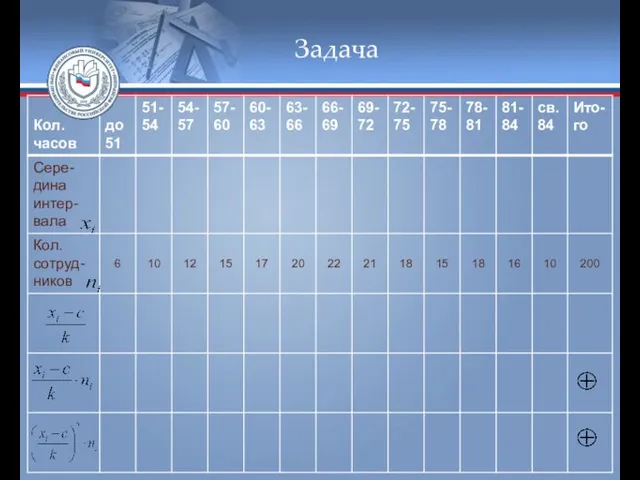
- 44. Задача Пример 1. Для исследования количества рабочих часов, выработанных одним работником на фирме в течение декады
- 45. Задача Найти доверительную вероятность того, что среднее количество рабочих часов всех сотрудников отклонится от выборочной средней
- 46. Задача Рассмотреть повторную и бесповторную выборки. Проверить гипотезу о том, что количество рабочих часов, выработанных рабочим
- 47. Задача
- 48. Задача
- 49. Задача
- 50. Задача Найдём средние квадратические ошибки:
- 51. Задача Подставим их в формулу доверительной вероятности:
- 52. Задача Для нахождения доверительного интервала нужно найти предельную ошибку выборки. Используем найденные ранее значения средних квадратических
- 53. Задача Найдём минимальный объём выборки.
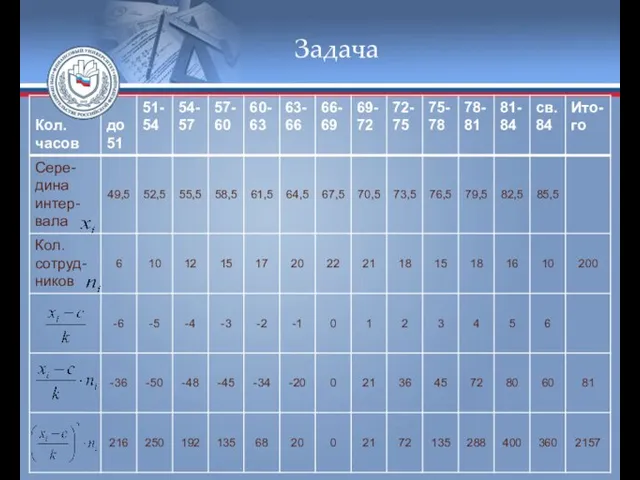
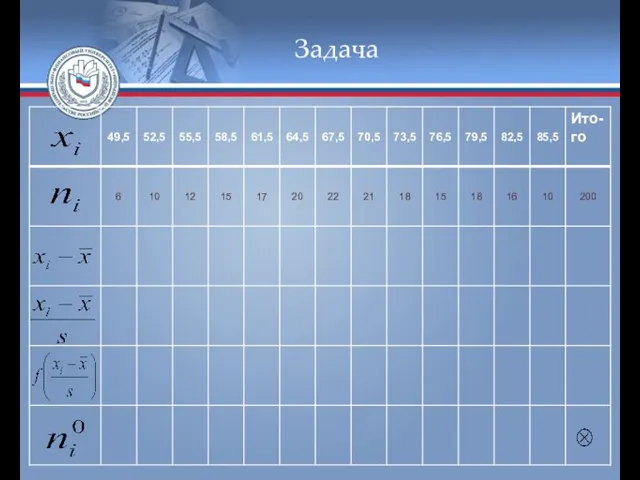
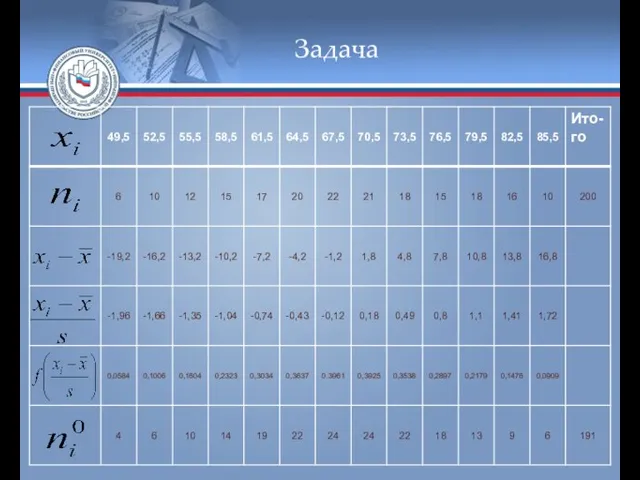
- 54. Задача Для нахождения теоретических частот составим вспомогательную таблицу
- 55. Задача
- 56. Задача
- 57. Задача Рассчитаем значение критерия Пирсона:
- 58. Задача Найдём по таблице критическое значение критерия Пирсона (число степеней свободы k=10, уровень значимости принимается равным
- 59. Задача Пример 2. Проверяется партия из 5000 консервов. Проверили 10%, среди проверенных оказалось 12% просроченных. Найти
- 60. Задача Каким должен быть минимальный объём выборки по которой можно было бы утверждать, что отклонение доли
- 61. Задача Решение: Дано:
- 62. Задача Для нахождения доверительного интервала найдём предельные ошибки выборки, используя найденные значения средних квадратических ошибок.
- 63. Задача Найдём минимальный объём выборки:
- 65. Скачать презентацию

























































 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Третий признак равенства треугольников. Урок 2
Третий признак равенства треугольников. Урок 2 Решение уравнений. Решение задач прикладного содержания
Решение уравнений. Решение задач прикладного содержания Перспектива. Построение перспективы
Перспектива. Построение перспективы Формулы сокращенного умножения. Преобразование выражений
Формулы сокращенного умножения. Преобразование выражений Дроби. Нахождение части числа
Дроби. Нахождение части числа Свойства корня n-ой степени
Свойства корня n-ой степени Презентация по математике "ДРОБНЫЕ ВЫРАЖЕНИЯ (6 КЛАСС)" - скачать бесплатно
Презентация по математике "ДРОБНЫЕ ВЫРАЖЕНИЯ (6 КЛАСС)" - скачать бесплатно Магические квадраты
Магические квадраты Комплексные числа и последовательности комплексных чисел. Лекция № 1
Комплексные числа и последовательности комплексных чисел. Лекция № 1 Презентация по математике "Электронный сборник задач с решением «Любимые задачи на дроби»" - скачать
Презентация по математике "Электронный сборник задач с решением «Любимые задачи на дроби»" - скачать  Множества. Операция над множествами
Множества. Операция над множествами Треугольник. Виды треугольников
Треугольник. Виды треугольников Обобщенный эвристический алгоритм
Обобщенный эвристический алгоритм Алгоритм сложения (вычитания) десятичных дробей
Алгоритм сложения (вычитания) десятичных дробей Теорема о вероятности суммы событий
Теорема о вероятности суммы событий Развертки. Развертка тетраэдра
Развертки. Развертка тетраэдра Прямоугольные координаты на плоскости
Прямоугольные координаты на плоскости Теория игр
Теория игр ПРЕЗЕНТАЦИЯ К УРОКУ МАТЕМАТИКИ В 6 КЛАСЕ «Взаимно обратные числа» ВЫПОЛНИЛА УЧИТЕЛЬ МАТЕМАТИКИ ПРОЩАЛЫГИНА Т.Г. 2012г.
ПРЕЗЕНТАЦИЯ К УРОКУ МАТЕМАТИКИ В 6 КЛАСЕ «Взаимно обратные числа» ВЫПОЛНИЛА УЧИТЕЛЬ МАТЕМАТИКИ ПРОЩАЛЫГИНА Т.Г. 2012г. Свойства параллельных прямых
Свойства параллельных прямых Тригонометрический круг
Тригонометрический круг Движение протяженных тел
Движение протяженных тел Разработал учитель математики МС(К)ОУ «С(К)О-ШИ № №3» Духова Т.Н.
Разработал учитель математики МС(К)ОУ «С(К)О-ШИ № №3» Духова Т.Н. Решение линейных неравенств
Решение линейных неравенств Бурттың жер көлемін анықтау
Бурттың жер көлемін анықтау Квадратные корни. Арифметический квадратный корень
Квадратные корни. Арифметический квадратный корень Математическая игра Что? Где? Когда?
Математическая игра Что? Где? Когда?