Содержание
- 2. Определение исчисления предикатов Определение 2.3. Функция одной или нескольких переменных, которая принимает логическое значение ”истина” или
- 3. Алфавит
- 4. Кванторы
- 5. Множество аксиом исчисления предикатов Аксиомы исчисления предикатов не содержат квантора существования. Для того, чтобы ввести в
- 6. Правила вывода исчисления предикатов
- 7. Теорема о дедукции исчисления предикатов
- 8. Теорема о дедукции исчисления предикатов
- 10. Теоремы о полноте Мы уже упоминали понятие общезначимости формул, понимая под ними такие формулы, которые принимают
- 11. Теоремы о полноте
- 12. Теоремы о полноте
- 13. Теоремы о полноте В отличие от исчисления высказываний для исчисления предикатов существует недоказуемая там формула, которую
- 14. Логическое следствие
- 15. Логическое следствие
- 16. Метод резолюций
- 18. Примеры применения метода резолюций Пример 1. Методом резолюций доказать теорему ├¬A→(A→ B) . Доказательство. Запишем инверсию
- 20. Скачать презентацию

















 Линейные ДУ n-го порядка
Линейные ДУ n-го порядка Слагаемые, сумма
Слагаемые, сумма Математика Тема: Сложение однозначных чисел с переходом через десяток, вида +7.
Математика Тема: Сложение однозначных чисел с переходом через десяток, вида +7. Теорема о трех перпендикулярах, ее применение при решении задач
Теорема о трех перпендикулярах, ее применение при решении задач Теорема Пифагора
Теорема Пифагора Иррациональные уравнения. Методы решения
Иррациональные уравнения. Методы решения Тема урока: «Новое свойство квадратных уравнений»
Тема урока: «Новое свойство квадратных уравнений» Дроби Дробь – это есть частное, делимое – числитель дроби, делитель – знаменатель. дроби. Любое натуральное число можно записать
Дроби Дробь – это есть частное, делимое – числитель дроби, делитель – знаменатель. дроби. Любое натуральное число можно записать  Уравнение окружности. Урок геометрии в 9 классе
Уравнение окружности. Урок геометрии в 9 классе Уравнения высших степеней (корни многочлена от одной переменной)
Уравнения высших степеней (корни многочлена от одной переменной) Производная. Применение производной в различных областях
Производная. Применение производной в различных областях Скалярное и векторное произведения векторов
Скалярное и векторное произведения векторов Создание проблемных ситуаций на уроках математики
Создание проблемных ситуаций на уроках математики Дифференциал функции
Дифференциал функции Архитектура и геометрия
Архитектура и геометрия Решение устных задач по готовым чертежам
Решение устных задач по готовым чертежам Уравнения с одним неизвестным
Уравнения с одним неизвестным Куб. Свойства куба
Куб. Свойства куба Координатная плоскость. Основные понятия
Координатная плоскость. Основные понятия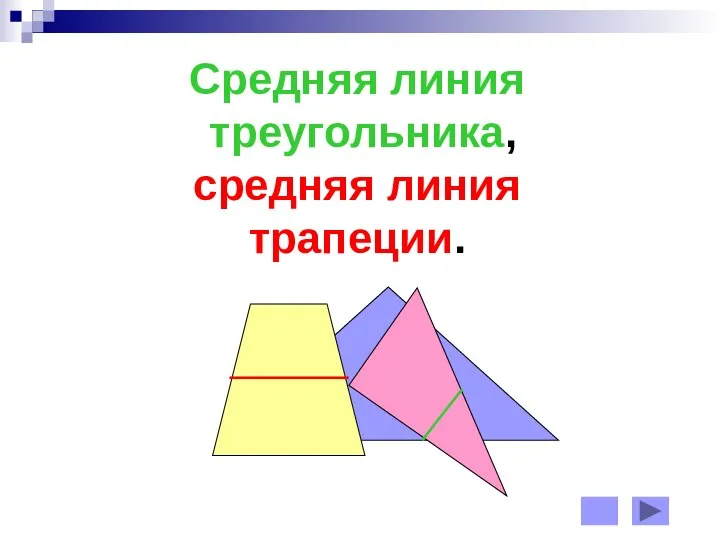 Cредняя линия треугольника, средняя линия трапеции
Cредняя линия треугольника, средняя линия трапеции Интеграл. Формула Ньютона – Лейбница
Интеграл. Формула Ньютона – Лейбница Нахождение неизвестного числа в равенствах вида: х+5=7. 4 класс
Нахождение неизвестного числа в равенствах вида: х+5=7. 4 класс Устный счет
Устный счет  возведение в квадрат суммы и разности двух выражений. Формула квадрата суммы
возведение в квадрат суммы и разности двух выражений. Формула квадрата суммы Понятие логарифма
Понятие логарифма Ряды Фурье Лекции 15, 16
Ряды Фурье Лекции 15, 16  Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Descriptive statistics. Elementary statistics. Larson. Farber. (Chapter 2)
Descriptive statistics. Elementary statistics. Larson. Farber. (Chapter 2)