Содержание
- 2. определена Пример : в точке x = 0 не определена , но Предел функции Повтор лекции
- 3. Первый замечательный предел Рассмотрим окружность единичного радиуса, х - центральный угол, 0 Повтор лекции 2
- 4. . При этом , т.е. последовательность возрастает и она ограничена : . Повтор лекции 2
- 5. Повтор лекции 2
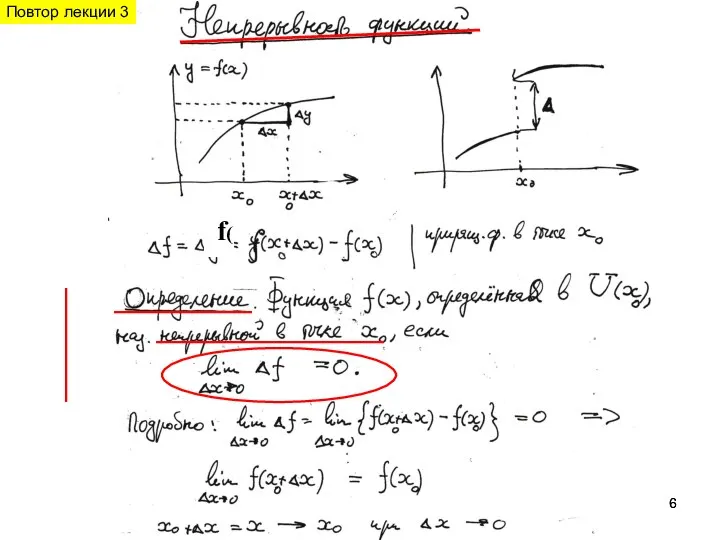
- 6. f( Повтор лекции 3
- 7. . 10 10 Повтор лекции 3 Повтор лекции 3
- 8. 1 2 3 4 5 Повтор лекции 3
- 9. . Повтор лекции 3
- 10. Точка разрыва первого рода – существование обоих односторонних конечных пределов ≡≡≡≡ ≡≡≡≡ Рис. 9.4
- 11. Продолжение. Если
- 12. Примеры
- 13. ≡≡
- 14. .
- 16. Производная функции В
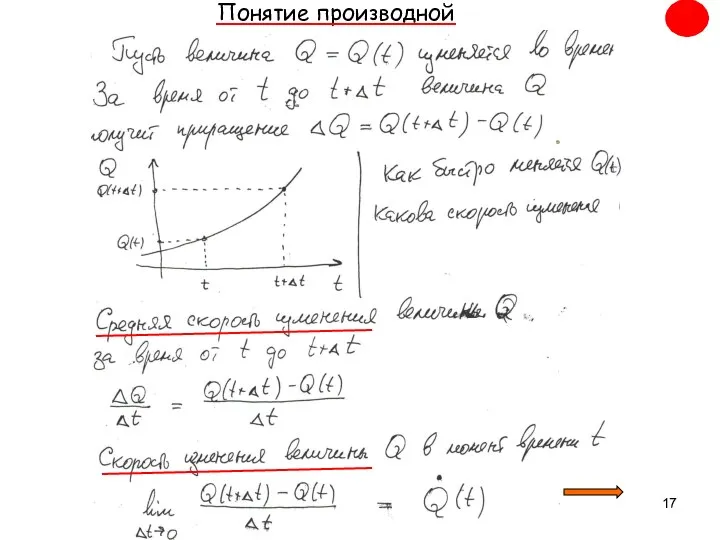
- 17. Понятие производной
- 18. . Таким образом, приходим к важнейшему понятию : Определение. Пусть ф. f(x) определена в окр. т.
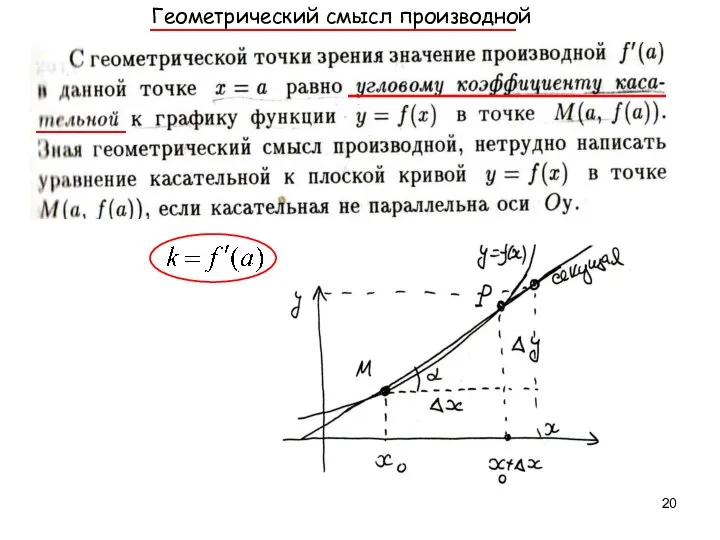
- 19. . ⎯⎯⎯⎯⎯⎯⎯ ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ ⎯⎯⎯ наз. предельное положение секущей при P M
- 20. Геометрический смысл производной
- 21. Основные правила дифференцирования
- 23. Тогда ≡≡≡ Производная обратной функции
- 25. Продолжение
- 26. ≡≡≡≡≡≡
- 28. Дифференциал функции
- 30. Экстремум функции
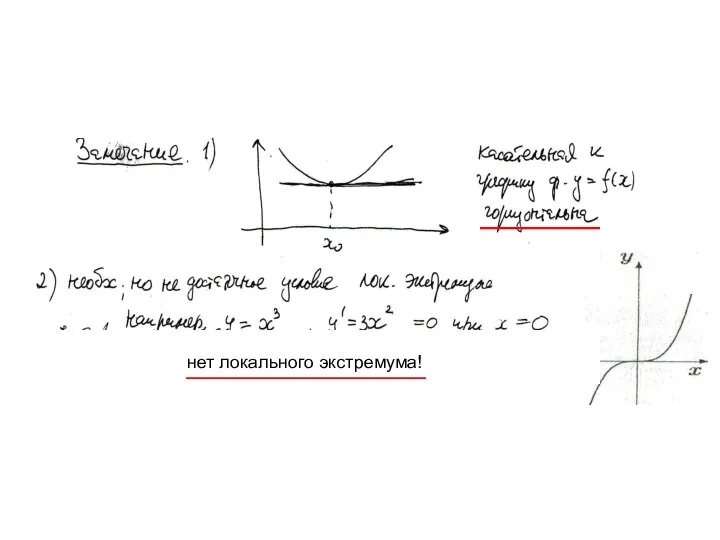
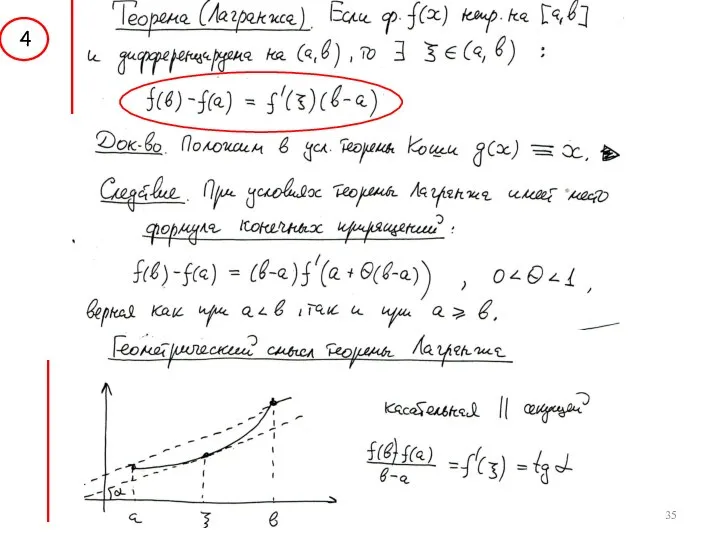
- 31. ____________________________________________ ____________ Основные теоремы дифференциального исчисления
- 32. нет локального экстремума!
- 33. по 2-й т. Вейерштасса по т. Ферма (слайд №) 2
- 34. 3
- 35. 4
- 36. Правило Лопиталя-Бернулли Теорема тогда ⇒ ) х) 5
- 40. Формула Тейлора является одной из жемчужин математического анализа и широко используется и в теоретических исследованиях, и
- 41. _______________________________________
- 44. Спасибо за внимание
- 45. Спасибо за внимание
- 46. Десять открытий в физике океана А.С. Монин, Н.Н. Корчагин Прикладная математика и . открытия в Мировом
- 48. .
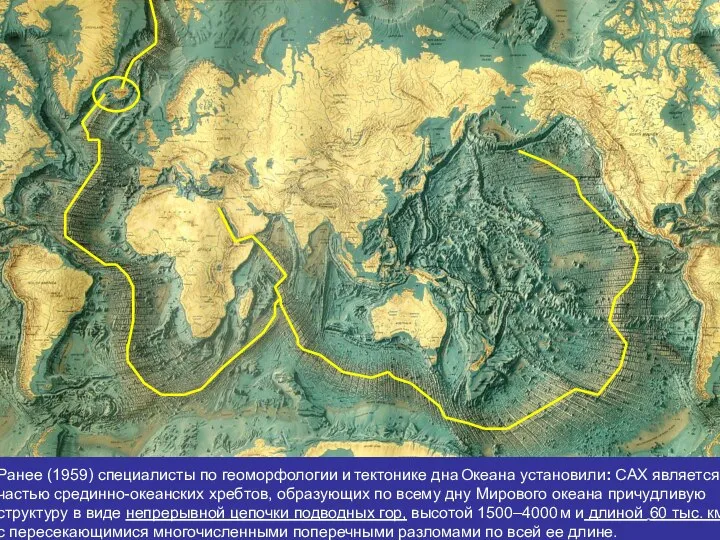
- 49. . . Ранее (1959) специалисты по геоморфологии и тектонике дна Океана установили: САХ является частью срединно-океанских
- 52. Скачать презентацию











































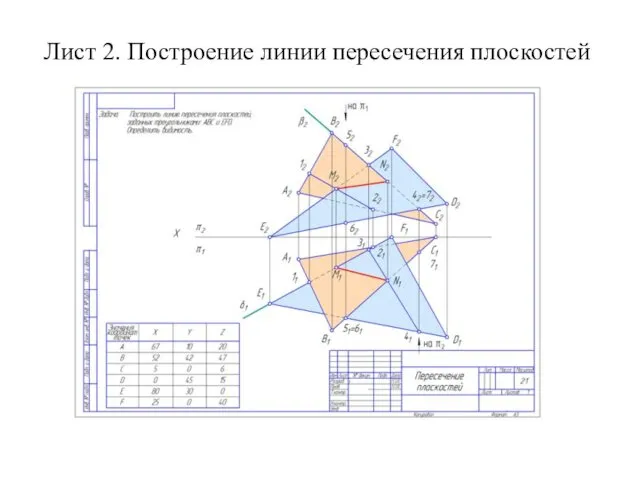 Построение линии пересечения плоскостей
Построение линии пересечения плоскостей Линейное уравнение с двумя неизвестными. 7 класс
Линейное уравнение с двумя неизвестными. 7 класс Треугольник
Треугольник Задачи на построение. Геометрия в 7-м классе
Задачи на построение. Геометрия в 7-м классе Его величество граф
Его величество граф Детектив ищет злодея. Математическая игра
Детектив ищет злодея. Математическая игра Теория вероятностей. События
Теория вероятностей. События Единицы измерения длины
Единицы измерения длины Ромб
Ромб Решение неравенств с одной переменной
Решение неравенств с одной переменной Ведение в вейлет преобразование
Ведение в вейлет преобразование Нахождение дроби от числа и числа по его дроби. 6 класс
Нахождение дроби от числа и числа по его дроби. 6 класс Метод Монте-Карло
Метод Монте-Карло Численное решение обыкновенных дифференциальных уравнений
Численное решение обыкновенных дифференциальных уравнений Презентация по математике "Немного о дробях" - скачать
Презентация по математике "Немного о дробях" - скачать  Комплeксные числа. Арифметические операции над ними (10 класс)
Комплeксные числа. Арифметические операции над ними (10 класс) Диаграммы, гистограммы, графики в Excel
Диаграммы, гистограммы, графики в Excel Окружность и круг
Окружность и круг Простейшие задачи в координатах
Простейшие задачи в координатах Письменное деление на числа, оканчивающиеся нулями
Письменное деление на числа, оканчивающиеся нулями Практические приложения подобия треугольников. О подобии произвольных фигур
Практические приложения подобия треугольников. О подобии произвольных фигур Проект «Числа в загадках, пословицах, поговорках, скороговорках»
Проект «Числа в загадках, пословицах, поговорках, скороговорках» Справочник по алгебре. (7-9 класс)
Справочник по алгебре. (7-9 класс) Уравнения и неравенства с параметрами. Часть 1
Уравнения и неравенства с параметрами. Часть 1 Графический способ решения квадратных уравнений Выполнил...
Графический способ решения квадратных уравнений Выполнил... Средняя линия треугольника
Средняя линия треугольника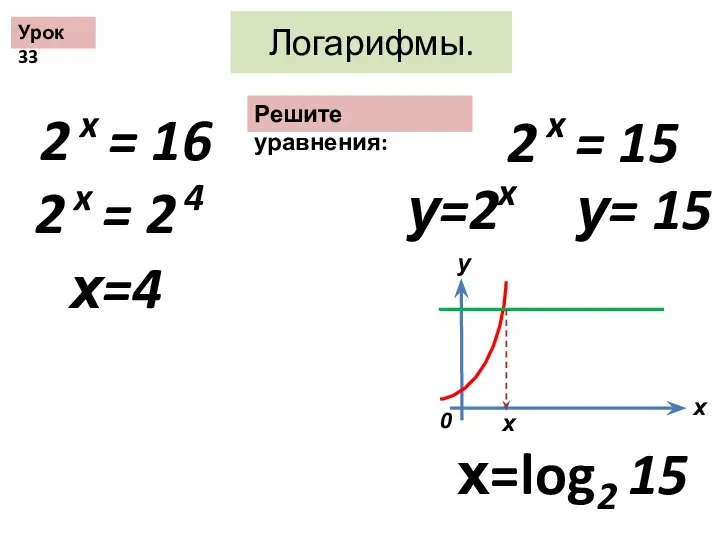 Логарифмы
Логарифмы Признаки подобия треугольников
Признаки подобия треугольников