Формы комплексного числа

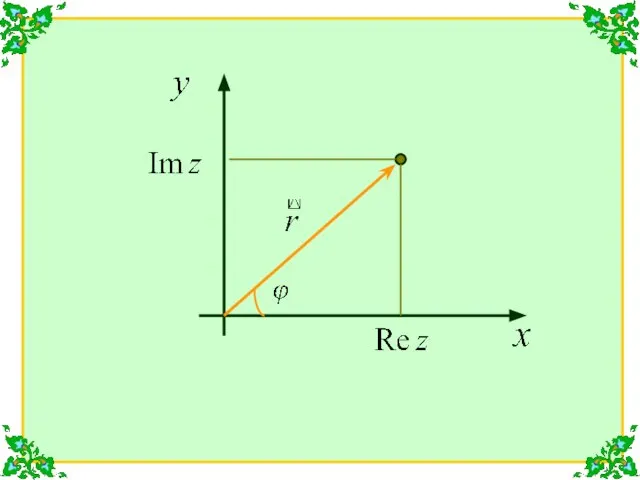
С каждой точкой комплексной плоскости связан радиус-вектор точки

Длина этого вектора

ПРИМЕР.

Поскольку

Из рисунка видно, что

Тогда

Выражение

называется тригонометрической формой комплексного числа.

2

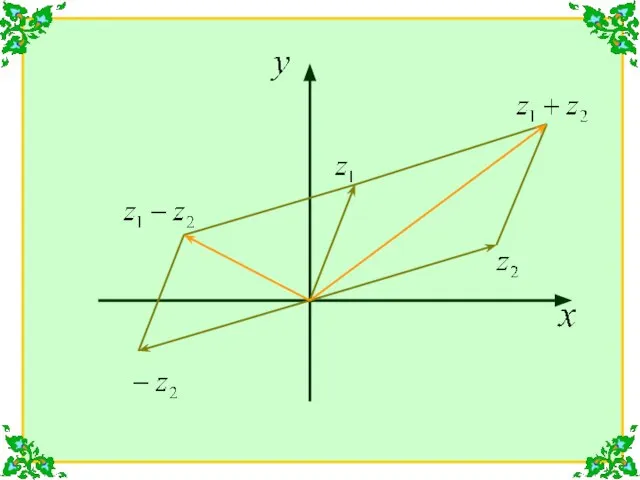
Свойства арифметических операций над комплексными числами

При сложении (вычитании) комплексных
чисел, их радиус-векторы

2

Модуль произведения (частного) двух
комплексных чисел равен произведению
(частному) модулей этих чисел, а

Если

тогда

Если

тогда

Геометрически умножение числа z1 на число z2 означает изменение длины радиус-вектора

ПРИМЕР.

Комплексные числа

представить в тригонометрической форме и найти их произведение и частное.

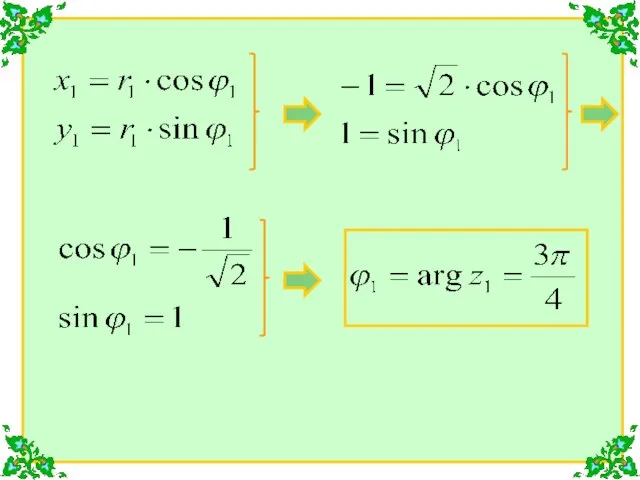
Решение.

Найдем модули этих комплексных чисел:

Теперь найдем аргументы этих комплексных чисел:

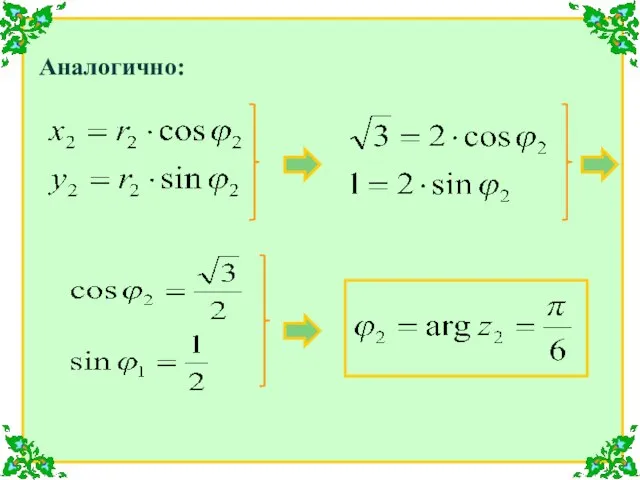
Аналогично:

Тогда в тригонометрической форме комплексные числа запишутся в виде:

Находим их произведение:

Находим их частное:

Т.к. при умножении комплексных чисел их модули перемножаются, а аргументы -

формула Муавра

ПРИМЕР.

Вычислить

Решение.

Запишем это число в тригонометрической форме:

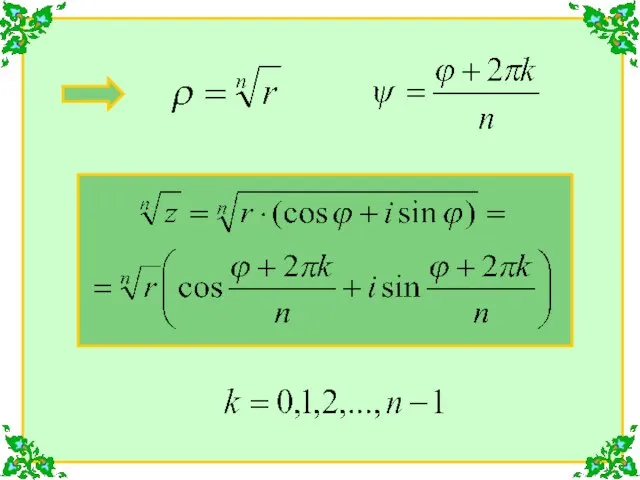
Рассмотрим операцию извлечения корня из комплексного числа. Пусть

тогда

следовательно

ПРИМЕР.

Вычислить

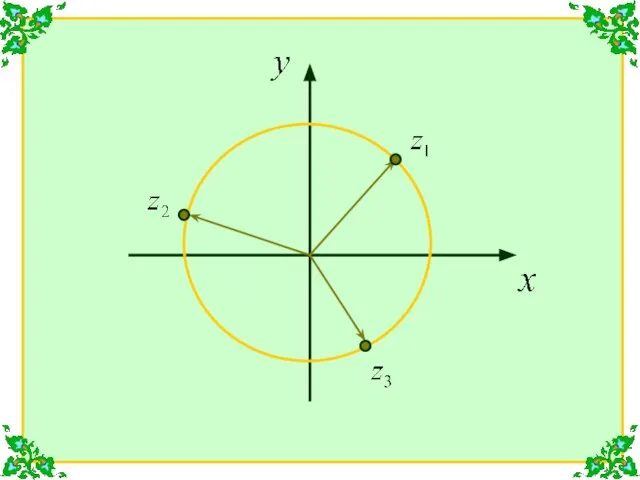
Решение.

Следовательно, получается три значения корня:

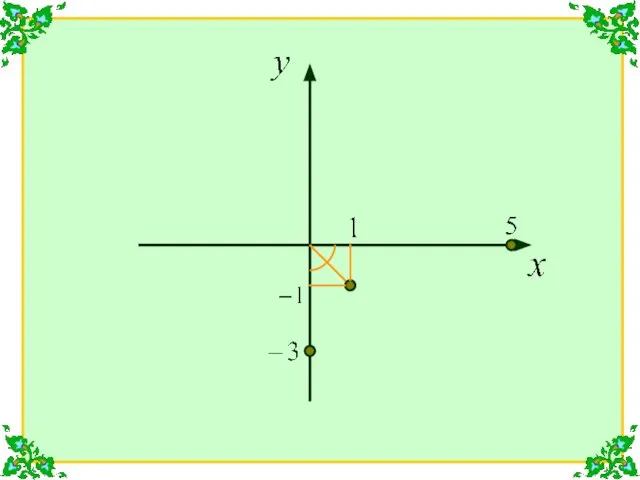
Изобразим эти точки на комплексной плоскости: