Содержание
- 2. Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, который основываясь на результатах Ферма и
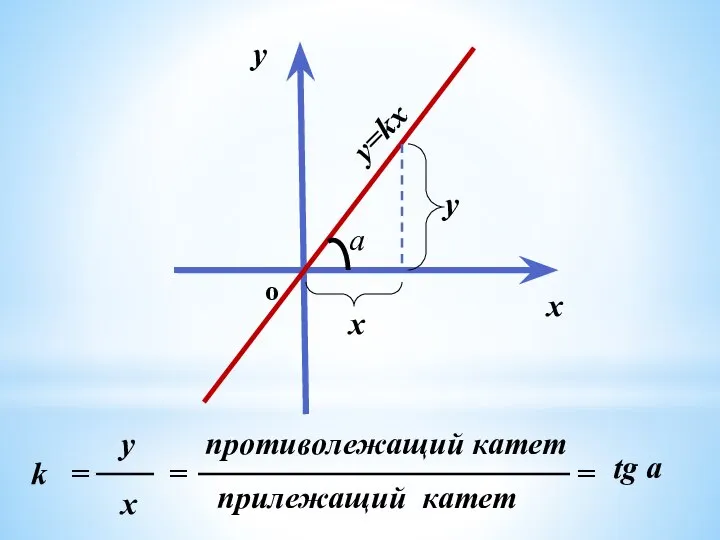
- 3. y=kx k = x y = противолежащий катет прилежащий катет = tg a a y x
- 4. k = tg a k – угловой коэффициент прямой а –угол между прямой и положительным направлением
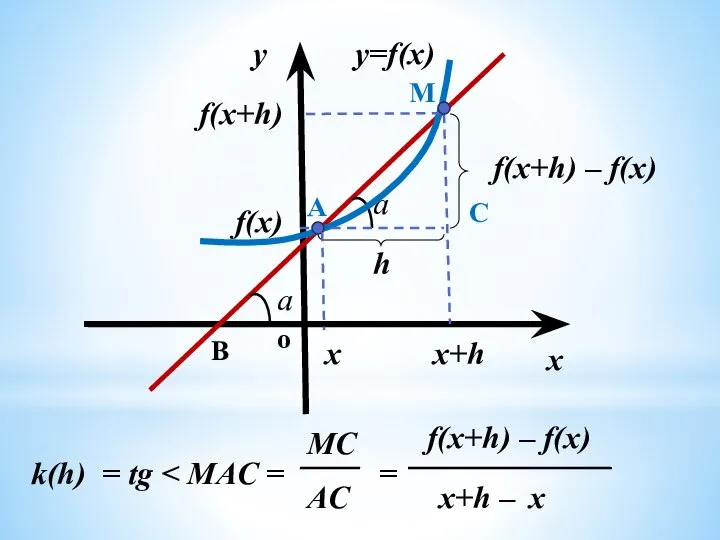
- 5. y=f(x) a x y x M B C A x+h f(x) f(x+h) f(x+h) – f(x) h
- 6. y=f(x) a x y x M B C A x+h f(x) f(x+h) f(x+h) – f(x) h
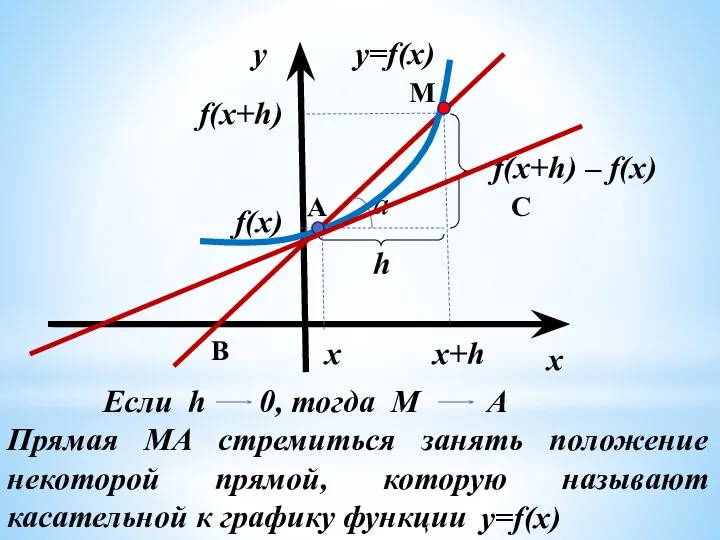
- 7. f(x+h) – f(x) x x+h – = lim k (h) f ' (x) k = tg
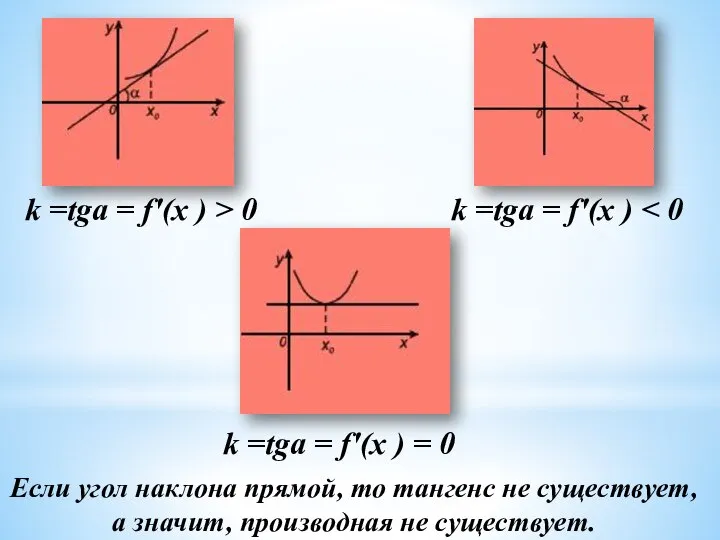
- 8. k =tga = f'(x ) k =tga = f'(x ) = 0 k =tga = f'(x
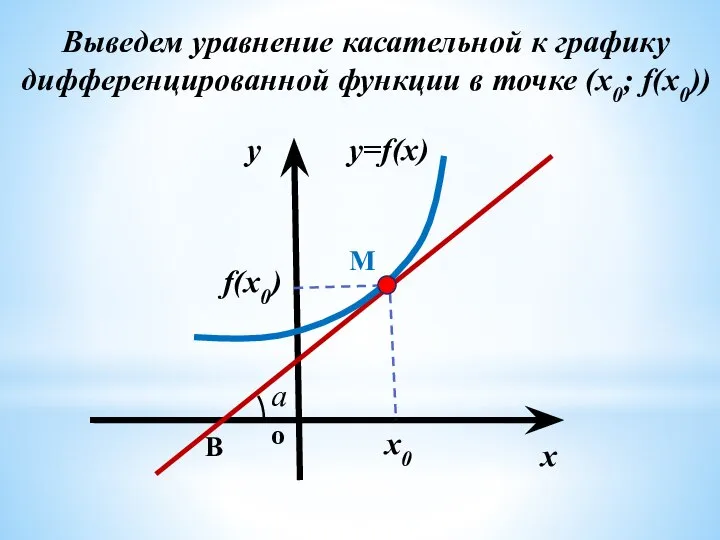
- 9. y=f(x) x0 y x B М f(x0) a o Выведем уравнение касательной к графику дифференцированной функции
- 10. y=kx +b k = tg a f ' (x) = y=f' (x0 )x+ b Т.к. касательная
- 12. Скачать презентацию




 Задания
Задания Системы n линейных уравнений с m неизвестными. Теорема Кронекера-Капелли. Методы их решения. Тема 3
Системы n линейных уравнений с m неизвестными. Теорема Кронекера-Капелли. Методы их решения. Тема 3 Геометрические фигуры. 5 класс
Геометрические фигуры. 5 класс Операционное исчисление
Операционное исчисление Сложение и вычитание смешанных чисел, 6 класс
Сложение и вычитание смешанных чисел, 6 класс Түзу мен жазықтықтың параллельдігі және перпендикулярлығы
Түзу мен жазықтықтың параллельдігі және перпендикулярлығы Диаграммы. Задачи
Диаграммы. Задачи Площади геометрических фигур. Задачи
Площади геометрических фигур. Задачи Математика и я. Язык математики – язык многих наук
Математика и я. Язык математики – язык многих наук Золотое сечение и симметрия
Золотое сечение и симметрия Автор : Пудовкина Светлана Николаевна Место работы : МОУ «Яншихово - Челлинская СОШ» Красноармейского района Чувашской Респу
Автор : Пудовкина Светлана Николаевна Место работы : МОУ «Яншихово - Челлинская СОШ» Красноармейского района Чувашской Респу Решение неравенств с одной переменной. 8 класс
Решение неравенств с одной переменной. 8 класс Таблица сложения чисел с переходом через десяток. Интерактивный тренажёр
Таблица сложения чисел с переходом через десяток. Интерактивный тренажёр Математические модели числа
Математические модели числа Знакомство с геометрическими фигурами. Круг
Знакомство с геометрическими фигурами. Круг Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Арифметические диктанты
Арифметические диктанты Сложение и вычитание десятичных дробей (5 класс)
Сложение и вычитание десятичных дробей (5 класс) Деление десятичных дробей
Деление десятичных дробей Муниципальное бюджетное образовательное учреждение Тогучинского района Горновская начальная общеобразовательная школа уро
Муниципальное бюджетное образовательное учреждение Тогучинского района Горновская начальная общеобразовательная школа уро Задачи на нахождение 4 пропорционального (3 класс)
Задачи на нахождение 4 пропорционального (3 класс) Цилиндр, конус, шар
Цилиндр, конус, шар Построение правильных многоугольников
Построение правильных многоугольников Конкретный смысл умножения
Конкретный смысл умножения Натуральные числа (N.). Простые и составные числа. Делитель, кратное
Натуральные числа (N.). Простые и составные числа. Делитель, кратное Решение задач с помощью графов
Решение задач с помощью графов Построение правильных многоугольников
Построение правильных многоугольников Закрепление изученного. Урок №78
Закрепление изученного. Урок №78