Содержание
- 2. Определения G(V,E) - связный неориентированный граф с заданной функцией стоимости, отображающей ребра в вещественные числа. Остовное
- 3. Алгоритм Краскала (Джозеф Крускал, 1956 год) Сортируем ребра графа по возрастанию весов. Полагаем, что каждая вершина
- 4. Время работы: Cортировка рёбер - O(|E|×log|E|) Компоненты связности удобно хранить в виде системы непересекающихся множеств. Все
- 5. Алгоритм Краскала Вход. Неориентированный граф G= (V, Е) с функцией стоимости с, заданной на его ребрах.
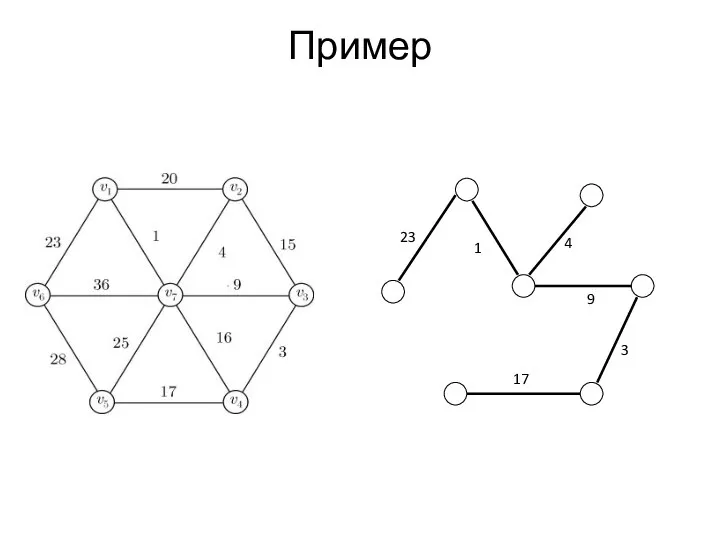
- 6. Пример м1 1 3 4 9 23 17
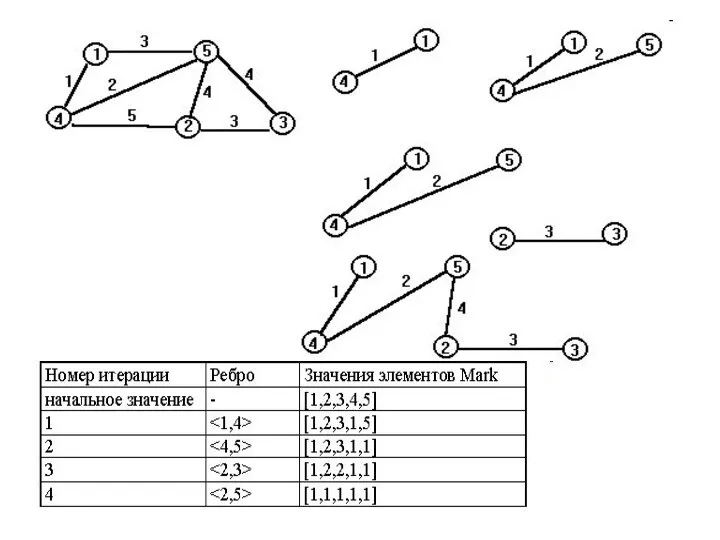
- 7. Получившееся дерево является каркасом минимального веса. Введем массив меток вершин графа Mark. Начальные значения элементов массива
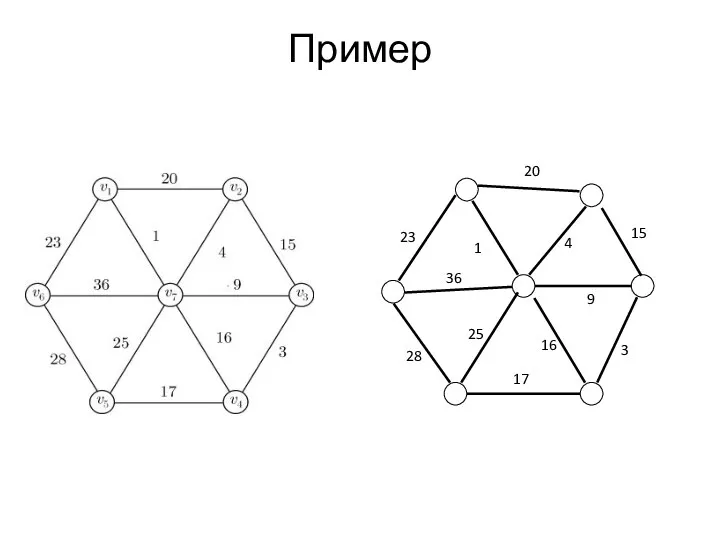
- 9. Алгоритм Прима На каждом шаге вычеркиваем из графа дугу максимальной стоимости с тем условием, что она
- 10. Пример м1 1 3 4 9 23 17 20 15 36 25 28 16
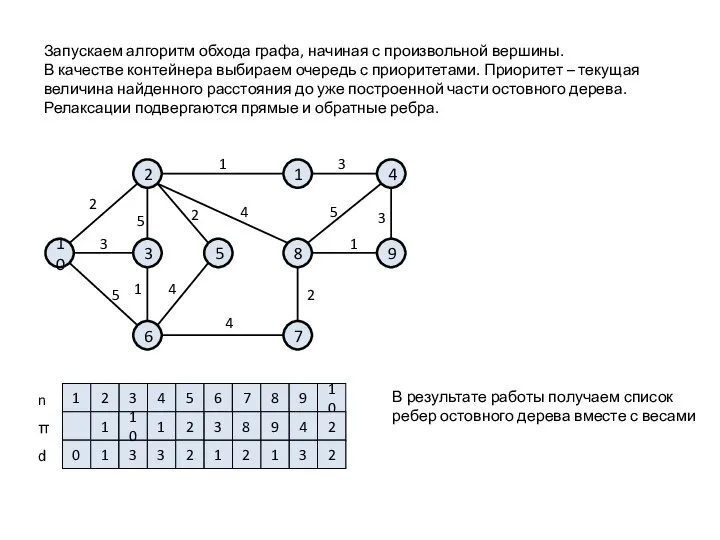
- 11. Алгоритм Прима ( Ярника, Дейкстры ) Алгоритм впервые был открыт в 1930 году чешским математиком Войцехом
- 12. 1) Выбирается произвольная вершина - она будет корнем остовного дерева; 2) Измеряется расстояние от нее до
- 13. 10 2 3 6 1 8 5 7 4 9 1 1 1 2 2 2
- 14. Реализация за O (M log N + N2) Отсортируем все рёбра в списках смежности каждой вершины
- 15. Система непересекающихся множеств (СНМ) Система непересекающихся множеств — это структура данных, которая реализует разбиение множества. Каждое
- 16. СНМ поддерживает следующие операции: MakeSet (x) — добавляет в СНМ новый элемент x, который заносится в
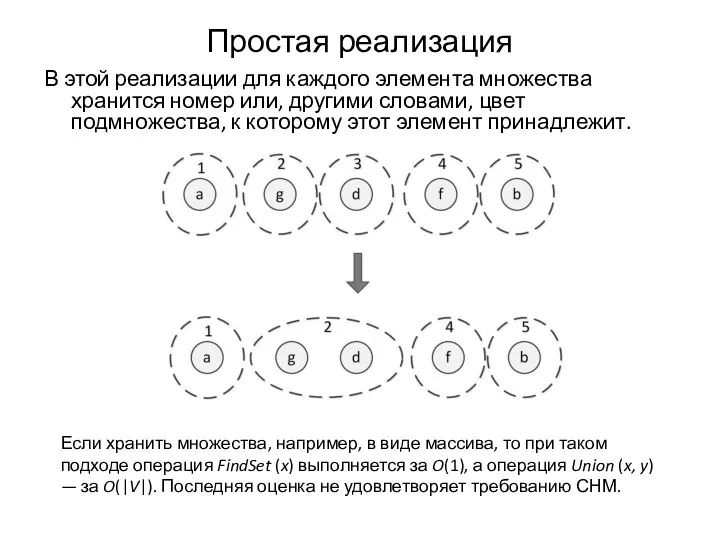
- 17. Простая реализация В этой реализации для каждого элемента множества хранится номер или, другими словами, цвет подмножества,
- 18. Реализация с помощью списков 1 способ. Если хранить множества в виде линейных списков с указателями на
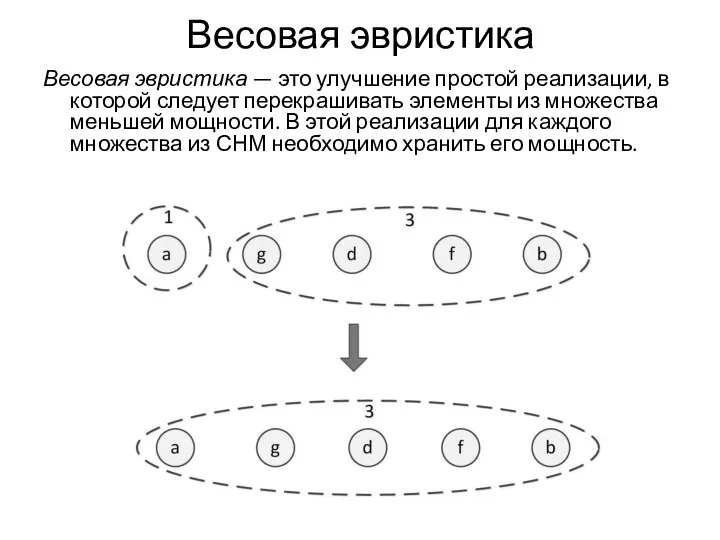
- 19. Весовая эвристика Весовая эвристика — это улучшение простой реализации, в которой следует перекрашивать элементы из множества
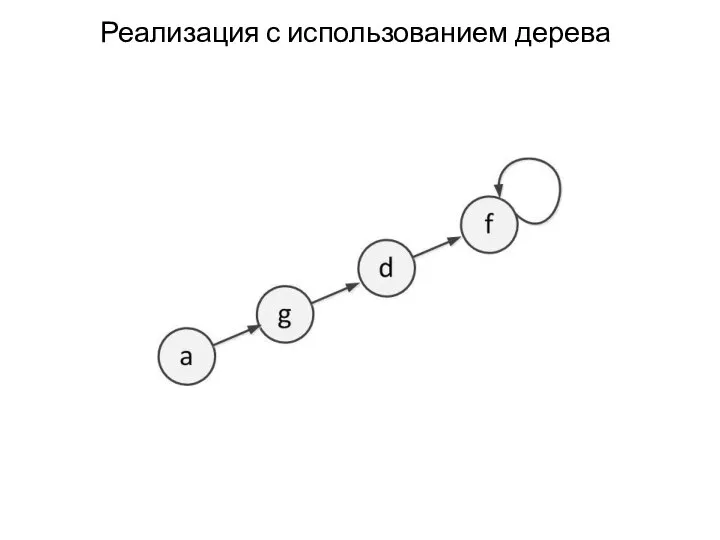
- 20. Реализация с использованием дерева
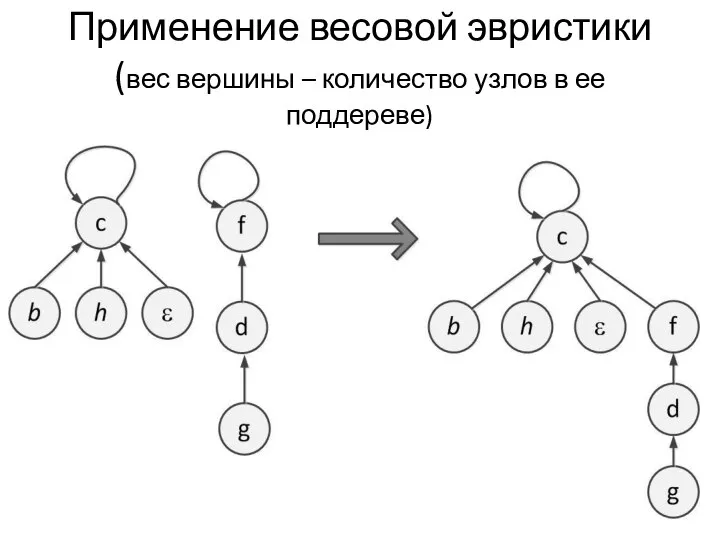
- 21. Применение весовой эвристики (вес вершины – количество узлов в ее поддереве)
- 22. Если размер дерева равен k, то его высота не более ⎣log k⎦ . Доказательство по индукции:
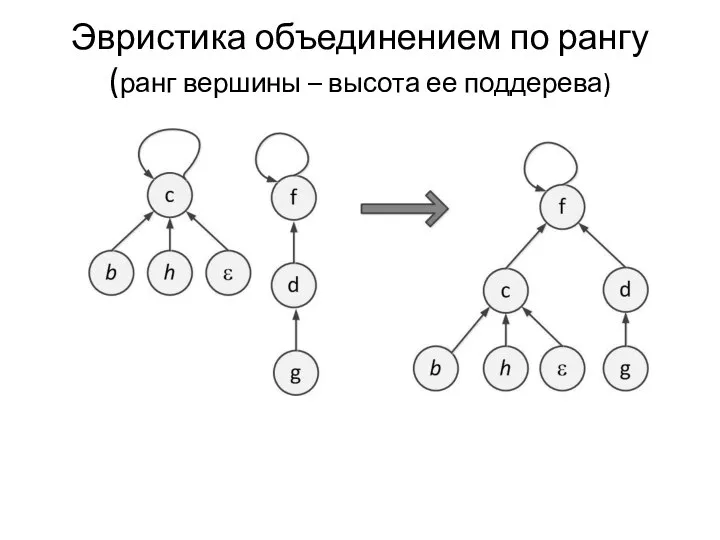
- 23. Эвристика объединением по рангу (ранг вершины – высота ее поддерева)
- 24. При применении ранговой эвристики получаем дерево высоты O(log n) Покажем, что если ранг дерева равен k,
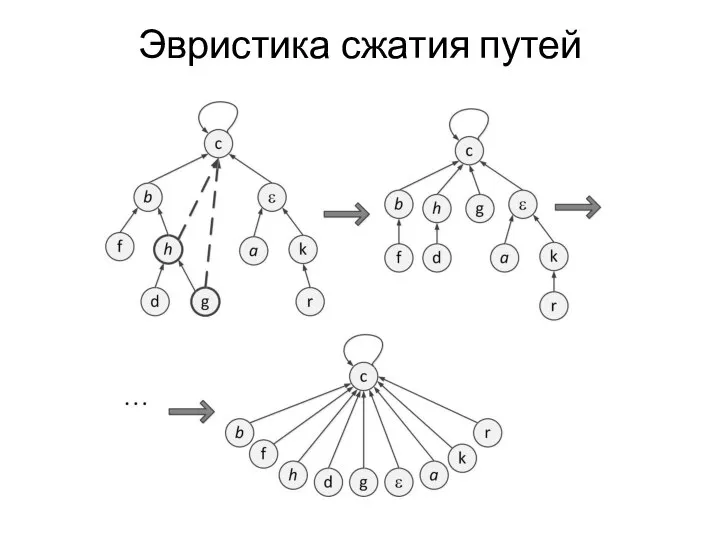
- 25. Эвристика сжатия путей
- 26. Пример реализации СНМ const int MAXN = 1000; int p[MAXN], rank[MAXN]; void makeset (int x) {
- 28. Скачать презентацию














![Пример реализации СНМ const int MAXN = 1000; int p[MAXN], rank[MAXN];](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1469055/slide-25.jpg)
 Алгоритм перевода десятичной записи числа в запись в позиционной системе с заданным основанием
Алгоритм перевода десятичной записи числа в запись в позиционной системе с заданным основанием Временные ряды
Временные ряды Готовимся к ЕГЭ: задачи на проценты
Готовимся к ЕГЭ: задачи на проценты Многогранники. Основные понятия
Многогранники. Основные понятия Производная элементарных функций
Производная элементарных функций Прямая. Отрезок. Луч
Прямая. Отрезок. Луч Вычисление площадей плоских фигур
Вычисление площадей плоских фигур Задание с параметром
Задание с параметром Презентация по математике "двузначные числа" - скачать бесплатно
Презентация по математике "двузначные числа" - скачать бесплатно ПРИМЕНЕНИЕ СВОЙСТВ ДЕЙСТВИЙ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ Математика 6 класс
ПРИМЕНЕНИЕ СВОЙСТВ ДЕЙСТВИЙ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ Математика 6 класс Несобственные интегралы, зависящие от параметра
Несобственные интегралы, зависящие от параметра Треугольники. Треугольник в науке
Треугольники. Треугольник в науке Решение уравнений
Решение уравнений Численные меоды. Вычислительная математика
Численные меоды. Вычислительная математика Комплексные числа
Комплексные числа Координаты вокруг нас Выполнил : Н. Бреев Тамбов 2007
Координаты вокруг нас Выполнил : Н. Бреев Тамбов 2007 Модуль «АЛГЕБРА» №7 Автор презентации: Гладунец Ирина Владимировна учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой об
Модуль «АЛГЕБРА» №7 Автор презентации: Гладунец Ирина Владимировна учитель математики МБОУ гимназии №1 г.Лебедянь Липецкой об Координатный луч (2)
Координатный луч (2) Площадь многоугольника
Площадь многоугольника Презентация по математике "Меры длины на Руси" - скачать
Презентация по математике "Меры длины на Руси" - скачать  Осевая и центральная симметрия
Осевая и центральная симметрия Матрицы и действия на ними
Матрицы и действия на ними Арифметические действия
Арифметические действия Распределительное свойство умножения
Распределительное свойство умножения Сказка про точку. (1 класс)
Сказка про точку. (1 класс) Знакомьтесь, открытые задачи. Мастер-класс
Знакомьтесь, открытые задачи. Мастер-класс Решение уравнений
Решение уравнений Элективный курс «Алгебра модуля»
Элективный курс «Алгебра модуля»