Содержание
- 2. Шенноновская энтропия. Проблемы применения к индивидуальным объектам Энтропия — мера неопределенности некоторой системы, например, какого-либо эксперимента,
- 3. Новизна теории сложности Колмогорова В начале 1960-х гг. Колмогоров, Соломонов, Левин и другие ученые сформулировали способ
- 4. Колмогоровская сложность Пусть F – алгоритм, аргументами и результатами которого являются двоичные слова. Слово x является
- 5. Колмогоровская сложность
- 6. Колмогоровская сложность
- 7. Функция K является перечислимой сверху
- 8. Невычислимость Колмогоровской сложности. Идея доказательства от противного. Парадоксы Не существует такого алгоритма, который по данному слову
- 10. Скачать презентацию







 Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Деление десятичных дробей
Деление десятичных дробей Треугольник. Геометрия 7 класс. Урок решения задач
Треугольник. Геометрия 7 класс. Урок решения задач Ключевые задачи по теории вероятностей
Ключевые задачи по теории вероятностей Множества и операции над ними (9 класс)
Множества и операции над ними (9 класс) Одночлен и его стандартный вид
Одночлен и его стандартный вид Методы решения уравнений c модулем
Методы решения уравнений c модулем Подобные треугольники
Подобные треугольники Разложение на множители с помощью группировки
Разложение на множители с помощью группировки Учимся работать циркулем
Учимся работать циркулем «RCA» DEPARTMENT OF HUMANITARIAN DISCIPLINES CHANGES IN CUSTOMS TARIFF ON RUSSIAAS A RESULT OF MEMBERSHIP IN WTO Created by: Nenadyshina Tatyana Hropina Olga
«RCA» DEPARTMENT OF HUMANITARIAN DISCIPLINES CHANGES IN CUSTOMS TARIFF ON RUSSIAAS A RESULT OF MEMBERSHIP IN WTO Created by: Nenadyshina Tatyana Hropina Olga Объем пирамиды
Объем пирамиды Число и цифра 2
Число и цифра 2 Нахождение части от целого и целого по его части
Нахождение части от целого и целого по его части Тригонометрия. Тригонометрические функции двойного аргумента
Тригонометрия. Тригонометрические функции двойного аргумента Квадратные уравнения. Обобщающий урок
Квадратные уравнения. Обобщающий урок Векторы. Векторные величины
Векторы. Векторные величины Значение переменных верного равенства. Корни уравнений
Значение переменных верного равенства. Корни уравнений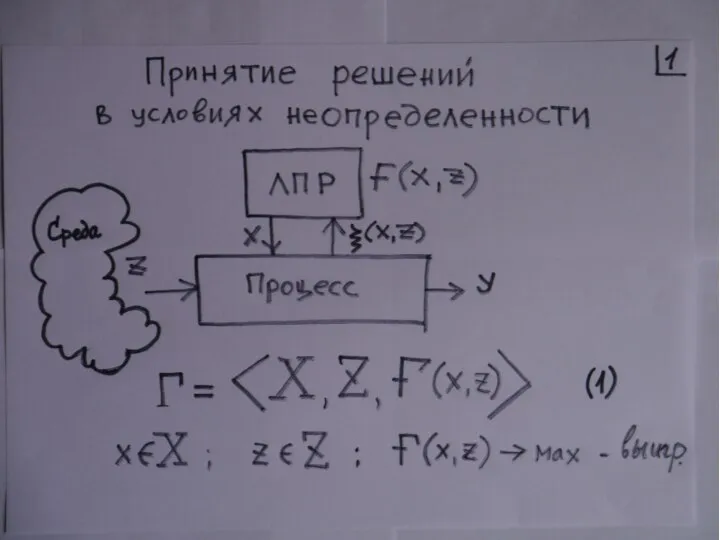 Принятие решений в условиях неопределенности
Принятие решений в условиях неопределенности Квадрат суммы и квадрат разности 7 класс Курсова
Квадрат суммы и квадрат разности 7 класс Курсова Организация исследовательской деятельности обучающихся на уроках математики
Организация исследовательской деятельности обучающихся на уроках математики Математика в жизни человека. Формирование устойчивого интереса к математике
Математика в жизни человека. Формирование устойчивого интереса к математике Презентация по математике "Деление У-2" - скачать
Презентация по математике "Деление У-2" - скачать  Масштаб
Масштаб Признаки делимости на 11
Признаки делимости на 11 Порядок выполнения действий в математике
Порядок выполнения действий в математике Сложение и вычитание десятичных дробей. (Урок 111)
Сложение и вычитание десятичных дробей. (Урок 111) Формулы понижения степени
Формулы понижения степени