Конечно-разностные методы решения систем уравнений, описывающих нестационарные режимы работы теплообменника
Содержание
- 3. Начальные условия: Граничные условия общего вида будут иметь следующий вид: ,
- 4. Явная конечно-разностная схема имеет вид:
- 5. Граничное условие: Начальные условия:
- 6. Схема устойчива при выполнении условия: Погрешность аппроксимации первого порядка:
- 7. Из конечно-разностных уравнений получаются следующие выражения для определения неизвестных значений температур потока и стенки:
- 8. Неявная конечно-разностная схема имеет вид:
- 9. т.е. известных значений В случае независимых граничных условий: , T1(0)=T10 T2(1)=T20
- 10. преобразовывая:
- 11. преобразовывая:
- 12. Из конечно-разностного аналога уравнения энергетического баланса для стенки выражается:
- 13. Подставляя в конечно-разностные уравнения теплового баланса потоков:
- 14. После преобразований получается:
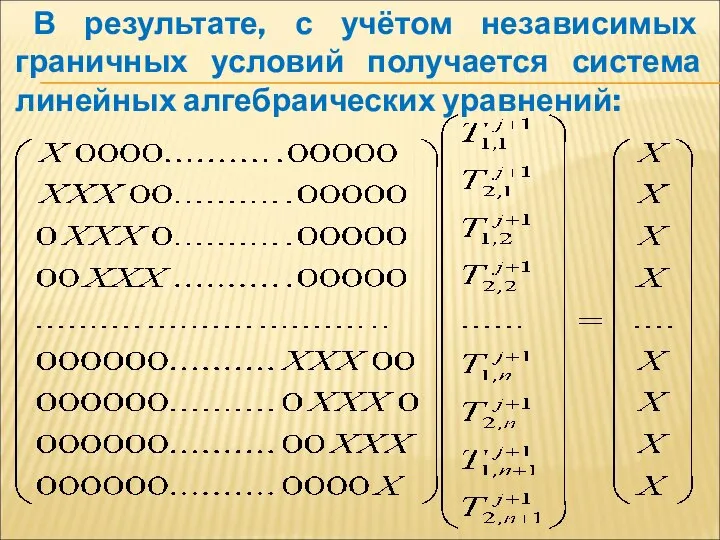
- 16. В результате, с учётом независимых граничных условий получается система линейных алгебраических уравнений:
- 17. Данная система решается с помощью метода прогонки на каждом шаге по времени. Если заданы граничные условия
- 19. Скачать презентацию













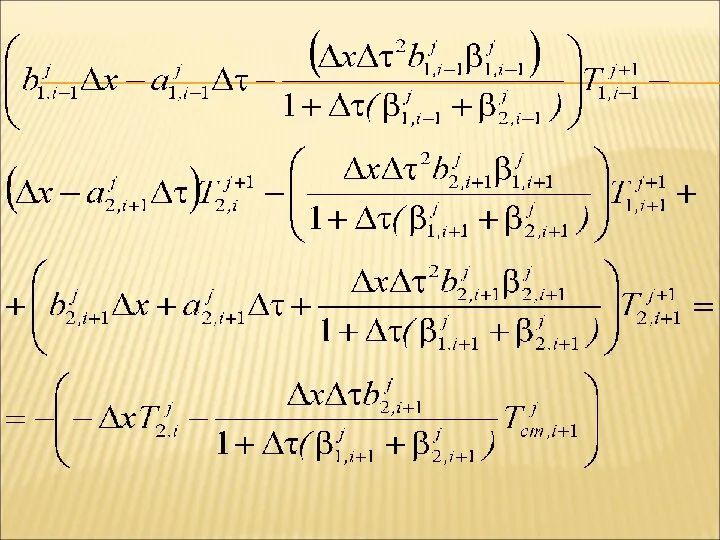

 Трапеция. Свойства
Трапеция. Свойства Проекция жазықтарын алмастыру әдісі
Проекция жазықтарын алмастыру әдісі Презентация на тему Сложение натуральных чисел и его свойства
Презентация на тему Сложение натуральных чисел и его свойства  Деление десятичных дробей на натуральное число
Деление десятичных дробей на натуральное число Понятие логарифма. Логарифм и его свойства
Понятие логарифма. Логарифм и его свойства Четность, нечетность, периодичность тригонометрических функций
Четность, нечетность, периодичность тригонометрических функций Реляционная алгебра
Реляционная алгебра Методы проверки ответа решенной задачи
Методы проверки ответа решенной задачи Таблица сложения
Таблица сложения Параллелепипед. Призма. Пирамида
Параллелепипед. Призма. Пирамида Числа от 11 до 20
Числа от 11 до 20 Пропорции. Проценты. Диаграммы
Пропорции. Проценты. Диаграммы Властивості прямокутного трикутника
Властивості прямокутного трикутника Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Параллелепипед
Параллелепипед Прямая пропорциональная зависимость
Прямая пропорциональная зависимость Дифференцирование функций комплексной переменной. Понятие аналитической функции
Дифференцирование функций комплексной переменной. Понятие аналитической функции Теорема Ербрана. (Лекция 4)
Теорема Ербрана. (Лекция 4) Презентация на тему Задачи на взвешивание
Презентация на тему Задачи на взвешивание Неделя математики. Открытая неделя - 2020
Неделя математики. Открытая неделя - 2020 Построение линии пересечения цилиндра и конуса
Построение линии пересечения цилиндра и конуса Оформление заданий по математике согласно федеральным образовательным стандартам Программа «школа 2100»
Оформление заданий по математике согласно федеральным образовательным стандартам Программа «школа 2100» Цікавий світ професій
Цікавий світ професій Формулы сокращенного умножения. (Найди ошибку) 7 класс
Формулы сокращенного умножения. (Найди ошибку) 7 класс Контрольно-измерительные инструменты для контроля плоскости
Контрольно-измерительные инструменты для контроля плоскости НОД чисел и НОК чисел
НОД чисел и НОК чисел Золотое сечение
Золотое сечение Розкриття дужок. Зведення подібних доданків
Розкриття дужок. Зведення подібних доданків