Содержание
- 2. Тема 5. Координаты и векторы I. Определение вектора. Основные понятия, связанные с векторами.
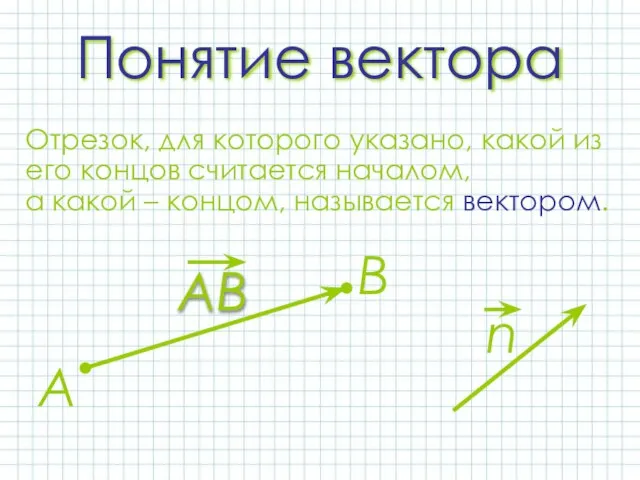
- 3. Понятие вектора А В Отрезок, для которого указано, какой из его концов считается началом, а какой
- 4. Нулевой вектор Любая точка на плоскости может рассматриваться как вектор. М Такой вектор называется нулевым.
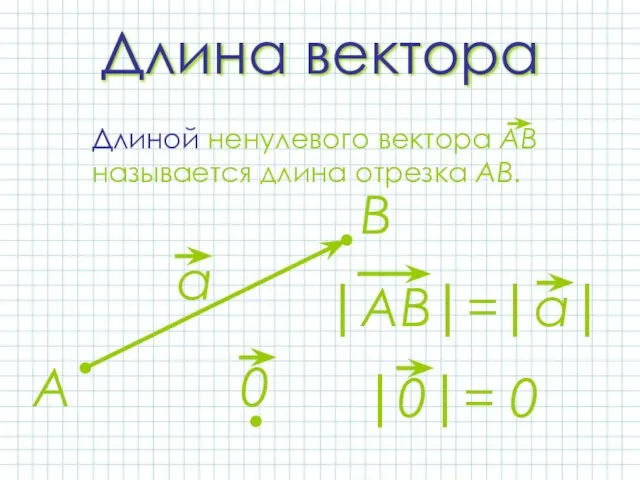
- 5. Длина вектора А В
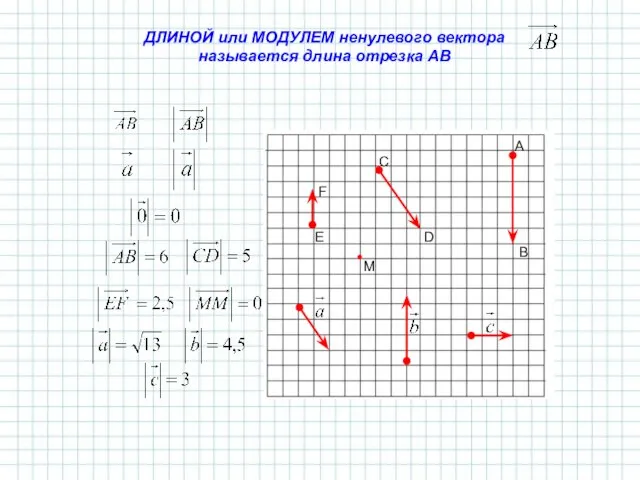
- 6. ДЛИНОЙ или МОДУЛЕМ ненулевого вектора называется длина отрезка АВ А B C D E F M
- 7. Как и в плоскости, в пространстве ВЕКТОР определяется как направленный отрезок: A B Точка А –
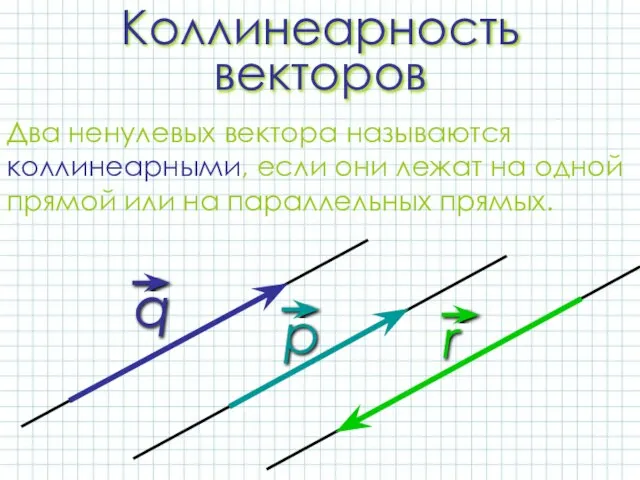
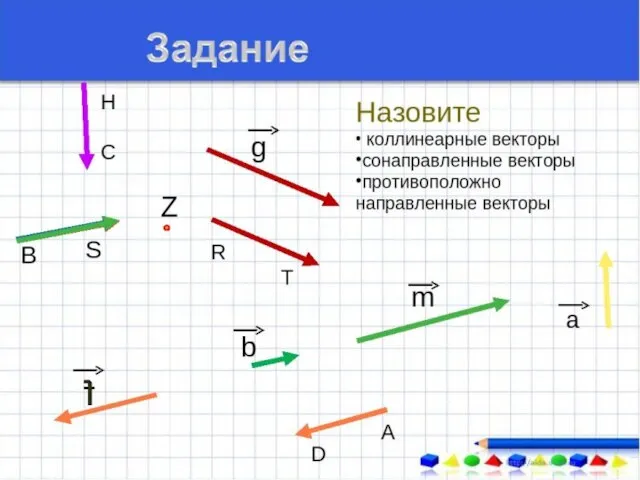
- 9. Коллинеарность векторов Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных
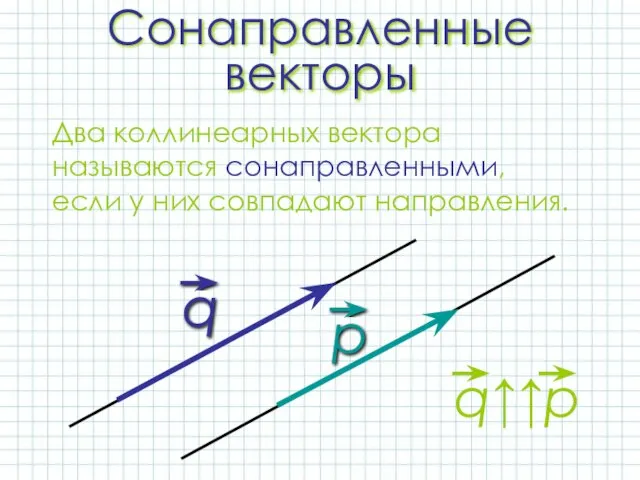
- 10. Сонаправленные векторы Два коллинеарных вектора называются сонаправленными, если у них совпадают направления.
- 11. Противоположно направленные векторы Два коллинеарных вектора называются противоположно направленными, если они не сонаправлены.
- 12. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых: a b
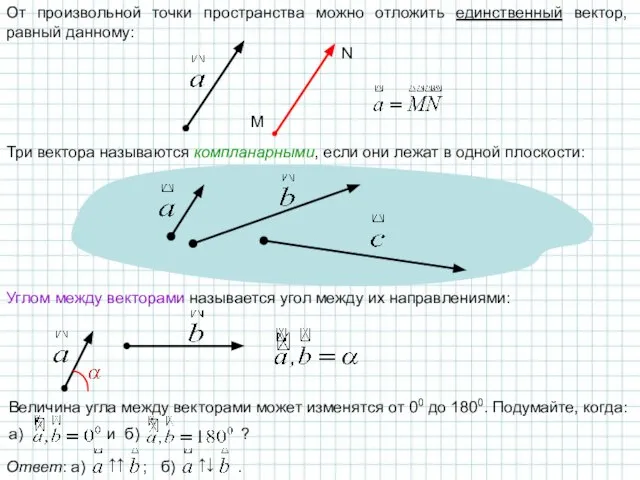
- 14. От произвольной точки пространства можно отложить единственный вектор, равный данному: M N Три вектора называются компланарными,
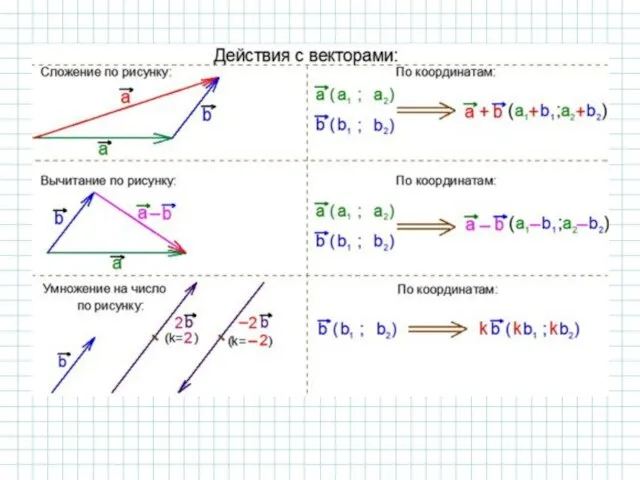
- 15. Тема 5. Координаты и векторы II. Действия с векторами
- 16. вектор отложен от точки А А ОТКЛАДЫВАЕНИЕ ВЕКТОРА ОТ ДАННОЙ ТОЧКИ https://youtu.be/DlLM97OvqsA
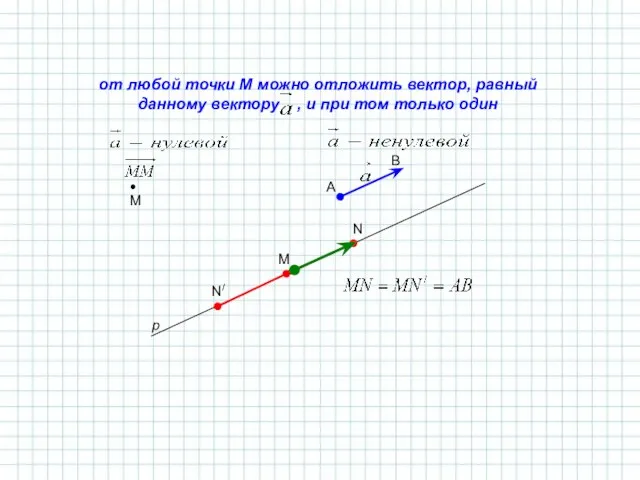
- 17. от любой точки М можно отложить вектор, равный данному вектору , и при том только один
- 18. Векторы можно складывать – в результате получается вектор. При сложении двух векторов применяются Правило треугольника: F
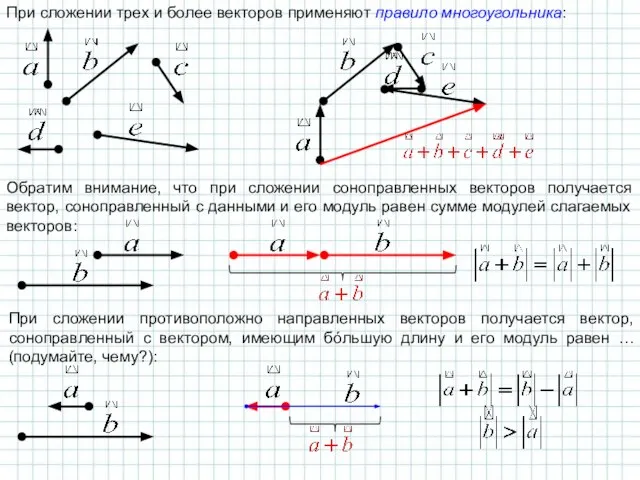
- 19. При сложении трех и более векторов применяют правило многоугольника: Обратим внимание, что при сложении соноправленных векторов
- 20. Также можно найти разность двух векторов – в результате получается вектор. При вычитании двух векторов применяется
- 21. Задача 1.
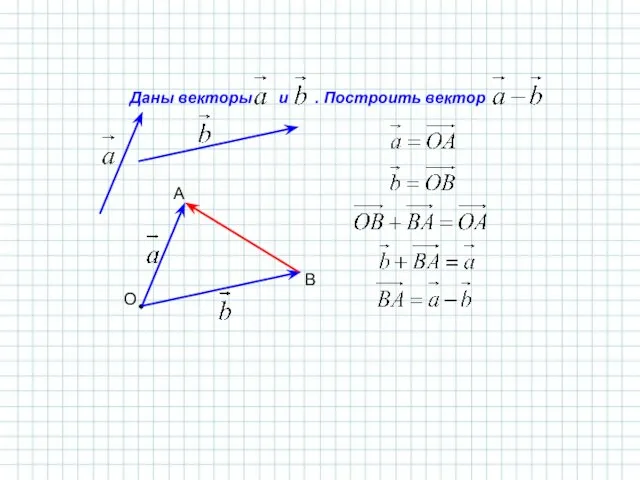
- 22. Даны векторы и . Построить вектор О А В
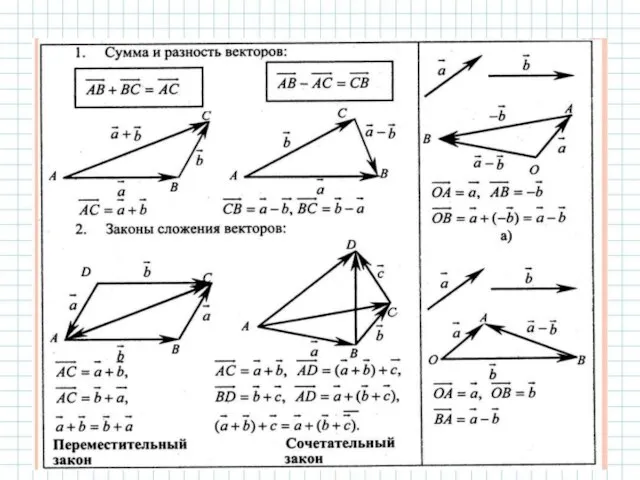
- 23. Сложение векторов, как и сложение чисел подчиняется законам: Следующее действие с векторами – умножение вектора на
- 24. И еще одно действие с векторами – умножение двух векторов. В школьном курсе геометрии изучается скалярное
- 26. Задача 2. Упростить выражение: Решение: Первый распределительный закон позволяет нам раскрыть скобки. А переместительное свойство сложения
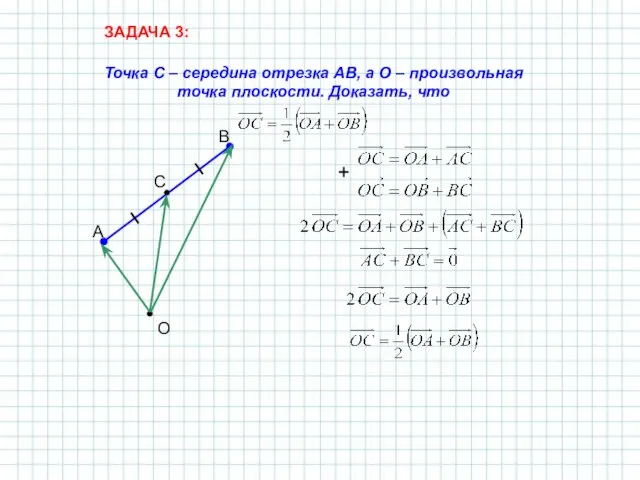
- 28. Точка С – середина отрезка АВ, а О – произвольная точка плоскости. Доказать, что A B
- 29. ЗАДАЧА 4: Доказать, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых
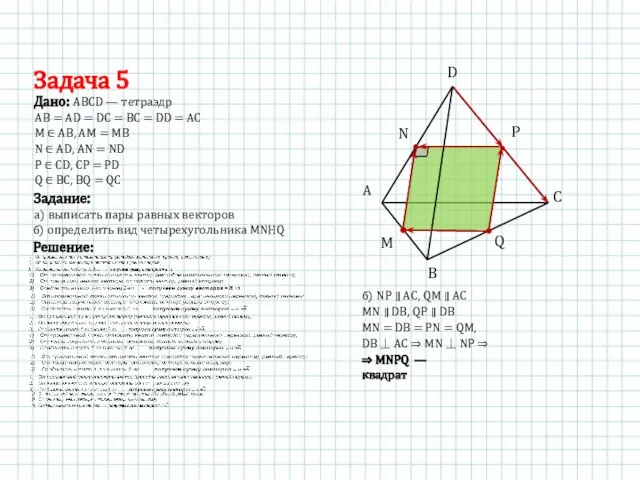
- 30. Задача 5 Дано: АВСD — тетраэдр Задание: N ∈ AD, AN = ND P ∈ СD,
- 32. Скачать презентацию














 Развитие самоконтроля на уроках математики
Развитие самоконтроля на уроках математики Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Дифференцирование показательной и логарифмической функций
Дифференцирование показательной и логарифмической функций Теорема Пифагора
Теорема Пифагора Использование средних статистических характеристик при решении различных задач. Алгебра 7 класс
Использование средних статистических характеристик при решении различных задач. Алгебра 7 класс Признаки параллелограмма
Признаки параллелограмма Функции. Определение функции
Функции. Определение функции Расчет пути и времени движения
Расчет пути и времени движения ОПЕРАЦИИ НАД одночленами Учитель математики СОШ №3 г. Вязники Владимирская область Стрелкова Ольга Алексеевна
ОПЕРАЦИИ НАД одночленами Учитель математики СОШ №3 г. Вязники Владимирская область Стрелкова Ольга Алексеевна Понятие корня квадратного из неотрицательного числа
Понятие корня квадратного из неотрицательного числа Численные методы безусловной оптимизации. Метода параллельных касательных, метод Пауэлла
Численные методы безусловной оптимизации. Метода параллельных касательных, метод Пауэлла Второй признак равенства треугольников
Второй признак равенства треугольников Методы многоскоростной обработки сигналов. Однократная децимация
Методы многоскоростной обработки сигналов. Однократная децимация Таблица классов и разрядов
Таблица классов и разрядов Параллелограмм
Параллелограмм Решение линейных уравнений с одной переменной
Решение линейных уравнений с одной переменной 10 новогодних задач. 5 класс
10 новогодних задач. 5 класс Деление трёхзначного числа на однозначное
Деление трёхзначного числа на однозначное Геометрическое истолкование производной
Геометрическое истолкование производной Уравнения с одной переменной
Уравнения с одной переменной Принадлежность точки выделенной области. 10 класс
Принадлежность точки выделенной области. 10 класс История возникновения нуля, его значение в жизни человека
История возникновения нуля, его значение в жизни человека Доминино
Доминино Обратная задача
Обратная задача Путешествие в сказку «Уравнения»
Путешествие в сказку «Уравнения»  Правила построения городского пейзажа с использованием линейной перспективы. 7 класс
Правила построения городского пейзажа с использованием линейной перспективы. 7 класс Счёт предметов. Цифра 5
Счёт предметов. Цифра 5 Путешествие в страну математики
Путешествие в страну математики