Содержание
- 2. Уравнения с одной переменной Пусть f(х) и g(х) – выражения с переменной. Равенство с переменной f(х)
- 3. Примеры: 3 + х = 7 ⇒ х = 4. Множество решений уравнения {4}. 2) (х
- 4. 4) (3х + 1) · 2 = 6х + 2⇒ 3) Уравнение х2 + 1 =
- 5. С точки зрения математической логики: Уравнением с одной переменной называется одноместный предикат f(х) = g(х), х
- 6. Пример: Множество значений переменной х, при которых f(х) и g(х) имеют определенные значения (имеют смысл), называют
- 7. Два уравнения f1(х) = g1(х) и f2(х) = g2(х) называются равносильными, если их множества решений равны,
- 8. 2) (2х + 1)·3 = 6х + 1, х2 + 1 = 0 Т1 = ∅,
- 9. Пусть даны два уравнения: f1(х) = g1(х), (1) f2(х) = g2(х). (2) Если множество решений уравнения
- 10. Пример: (х + 1)2 = 16, х + 1= 4. Т2 = {3} Два уравнения равносильны
- 11. ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ Теорема 1. Если к обеим частям уравнения f(х) = g(х), х∈Х (1)
- 12. 2) Пусть х = а – корень уравнения (2), т. е. f(а) + t(а) = g(а)
- 13. 1. Если к обеим частям уравнения прибавить одно и то же число, то получим уравнение, равносильное
- 14. Теорема 2. Если обе части уравнения f(х) = g(х), х ∈Х (1) умножить на выражение t(х),
- 15. Следствие. Если обе части уравнения умножить (или разделить) на одно и то же число, отличное от
- 16. Если же в процессе решения уравнения не выполняются условия теорем 1 и 2, то может произойти
- 17. Пример: х(х - 4)(х + 6)(х - 8)=0 ⇔ х = 0 ∨ х – 4
- 18. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ Уравнение вида ах = b называется линейным уравнением с одной переменной
- 19. Для линейного уравнения ах = b могут иметь место три случая: если а ≠ 0, то
- 20. Пример: ⇒ 8 + 3х + 2 - 2х = 5х - 12 3х – 2х
- 21. Графическое решение линейного уравнения первой степени ах = b ⇒ ах - b = 0 Построим
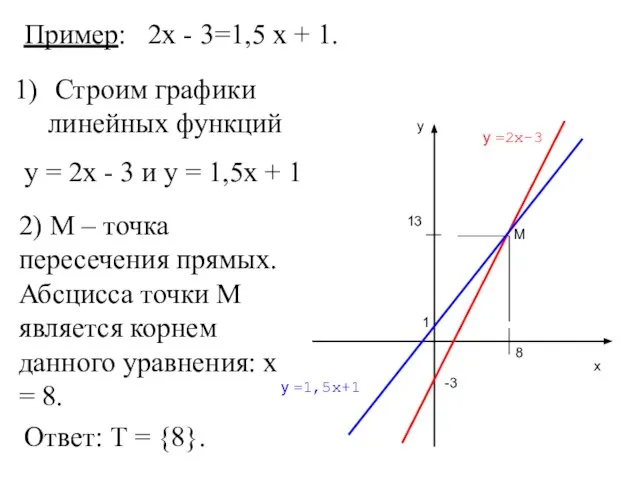
- 22. Пример: 2х - 3=1,5 х + 1. Строим графики линейных функций у = 2х - 3
- 23. Квадратное уравнение Уравнение вида ах2 + bх + с = 0, (1) где а, b, с
- 24. Неполные квадратные уравнения Если в квадратном уравнении b = 0, или с = 0, или b
- 25. Общая формула корней квадратного уравнения (2) ах2 + bх + с = 0 (1)
- 26. Выражение D = b2 – 4ас называют дискриминантом квадратного уравнения (1). Если D > 0, то
- 27. Приведенное квадратное уравнение Квадратное уравнение, у которого первый коэффициент равен 1, то есть уравнение вида х2
- 28. Теорема. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней
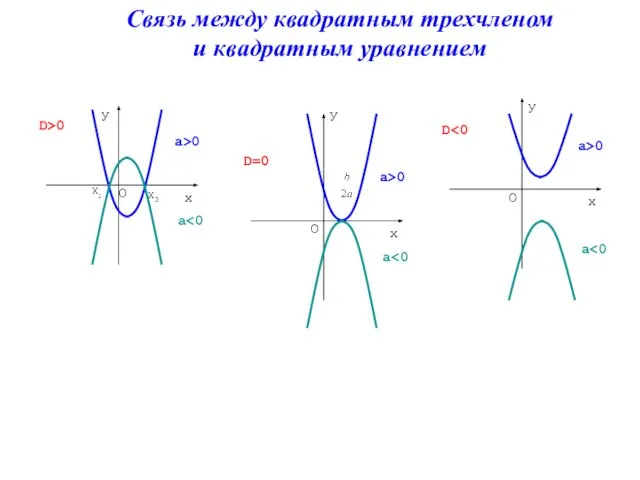
- 29. Связь между квадратным трехчленом и квадратным уравнением
- 30. Биквадратное уравнение Уравнение вида ах4 + bх2 + с = 0 (а ≠ 0) называется биквадратным.
- 31. Дробно- рациональные уравнения
- 32. Уравнение f(х) = g(х) называется дробно-рациональным, если f(х) и g(х) – рациональные выражения, хотя бы одно
- 33. Чтобы решить рациональное уравнение нужно: 1) найти область определения (или область допустимых значений) уравнения (приравнивая знаменатели
- 34. Пример: ОДЗ: Х = ]−∞; 0[ ∪ ]0; 2[ ∪ ]2; +∞[. 2 – х ≠
- 35. 2·2х + х(2 - х) = 4·2 4х + 2х – х2 = 8 х2 –
- 36. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ Общий порядок решения задач с помощью уравнений таков: 1. Вводят переменные,
- 37. 3. Решают составленное уравнение (или систему уравнений) и из полученных решений отбирают те, которые подходят по
- 38. Задачи на движение Моторная лодка, собственная скорость которой 20 км/ч, прошла расстояние между двумя пунктами по
- 40. 60 · 4·(20 - х) + 60 · 4 ·(20 + х) = 25 ·(20 +
- 41. Задачи на совместную работу
- 42. Двое рабочих, работая вместе, выполнили некоторую работу за 6 ч. Первый из них, работая отдельно, может
- 43. 6х + 30 + 6х = х2 + 5х
- 44. х2 – 7х – 30 = 0 х1 = 10, х2 = - 3 – посторонний
- 45. Равенство с двумя переменными f(х, у) = 0 или f(х, у) = g(х, у) называется уравнением
- 46. Пример: х – 3у = 10. (10; 0), (16; 2), (- 2; - 4) - решения
- 47. С логической точки зрения: Уравнением с двумя переменными называется двухместный предикат f(х, у) = 0 или
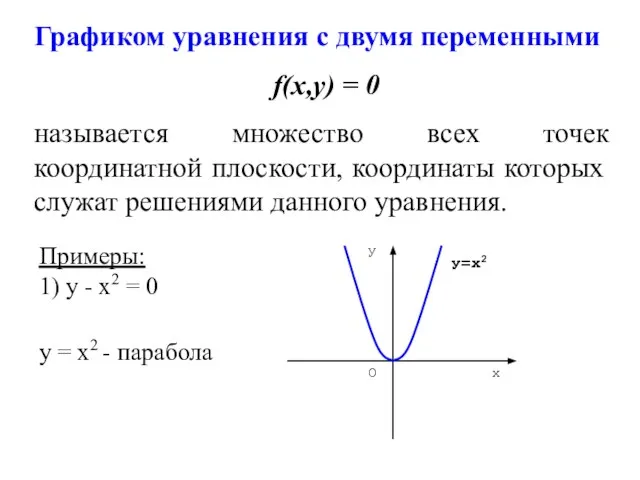
- 48. Графиком уравнения с двумя переменными f(х,у) = 0 называется множество всех точек координатной плоскости, координаты которых
- 49. 2) у – х = 0 у = х - прямая точка (1; 2) 3) Итак,
- 50. Линейное уравнение с двумя переменными Уравнение вида ах + bу = с называется линейным уравнением с
- 51. Выразим у через х: (b ≠ 0) – линейная функция, ее графиком является прямая. Если b
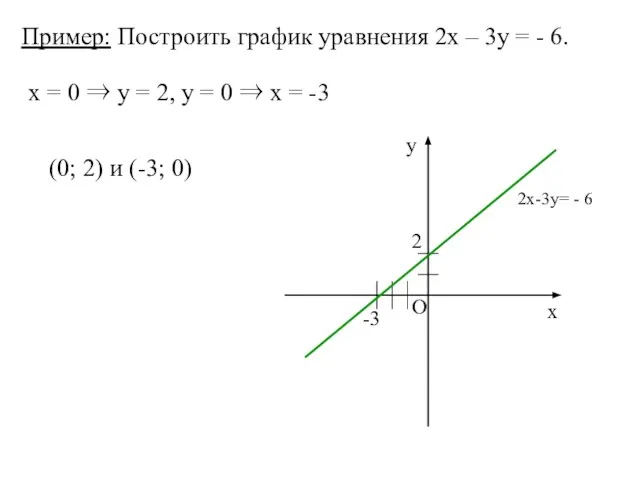
- 52. Пример: Построить график уравнения 2х – 3у = - 6. х = 0 ⇒ у =
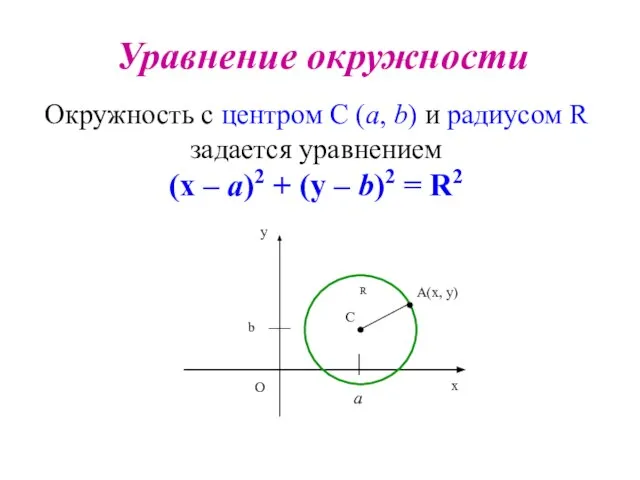
- 53. Уравнение окружности Окружность с центром С (а, b) и радиусом R задается уравнением (х – а)2
- 54. Примеры: 1) Записать уравнение окружности с центром С (-7; 6) и радиусом 5. (х + 7)2
- 55. 2) Доказать, что уравнение х2 + у2 – 6х + 8у – 75 = 0 является
- 56. 3) Составьте уравнение окружности, проходящей через точку А (1; - 1) с центром С(- 2; 3).
- 57. 4) Составить уравнение окружности с центром на прямой у = 4, касающейся оси Ох в точке
- 59. Скачать презентацию






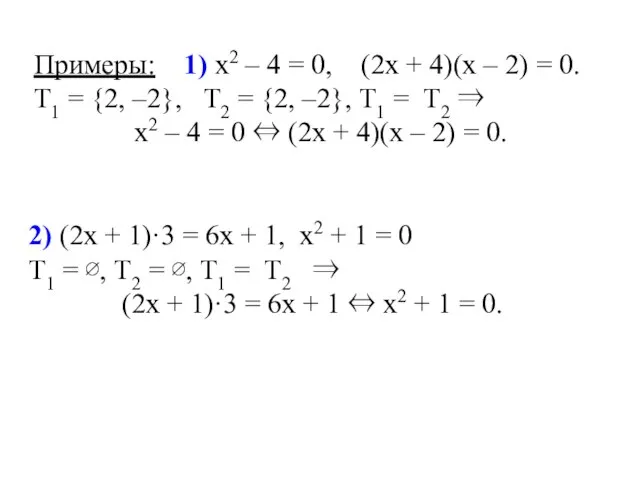























![Пример: ОДЗ: Х = ]−∞; 0[ ∪ ]0; 2[ ∪ ]2;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/570089/slide-33.jpg)




















 Дисперсионный анализ
Дисперсионный анализ Решение задач» для 6 класса от героев мультиков
Решение задач» для 6 класса от героев мультиков Методическая разработка по выполнению исследовательской работы на тему: «Логические задачи»
Методическая разработка по выполнению исследовательской работы на тему: «Логические задачи» Презентация на тему Сложение и вычитание чисел
Презентация на тему Сложение и вычитание чисел  Математик – бизнесмен. Математическая игра для 7 классов
Математик – бизнесмен. Математическая игра для 7 классов Представление трехзначных чисел в виде суммы разрядных слагаемых
Представление трехзначных чисел в виде суммы разрядных слагаемых Площадь поверхности конуса
Площадь поверхности конуса Вписанная и описанная пирамиды. Домашнее задание
Вписанная и описанная пирамиды. Домашнее задание Определение логарифма
Определение логарифма Линейные преобразования: основные понятия и определения
Линейные преобразования: основные понятия и определения Зачетная система в старших классах как средство предупреждения неуспеваемости
Зачетная система в старших классах как средство предупреждения неуспеваемости Презентация по математике "Анализ количественных признаков" - скачать бесплатно
Презентация по математике "Анализ количественных признаков" - скачать бесплатно Построение графиков функции y = sinx и y = cosx
Построение графиков функции y = sinx и y = cosx Окружность вписанная, описанная, вневписанная
Окружность вписанная, описанная, вневписанная Домашнее задание: по сборнику Ященко ( огэ математика 2021)
Домашнее задание: по сборнику Ященко ( огэ математика 2021) Прямоугольный параллелепипед. 5 класс
Прямоугольный параллелепипед. 5 класс Интерактивная игра-тренажёр Собери пазл (1 класс)
Интерактивная игра-тренажёр Собери пазл (1 класс) Prezentacii.com Урок математики в 6 классе Автор учитель математики, информатики Иванова Елена Васильевна МБОУ «СОШ №5 с углублённ
Prezentacii.com Урок математики в 6 классе Автор учитель математики, информатики Иванова Елена Васильевна МБОУ «СОШ №5 с углублённ Новейшие информационные технологии в управлении
Новейшие информационные технологии в управлении Сложение чисел с разными знаками
Сложение чисел с разными знаками Алгебра. Лекция 6. Классы вычетов
Алгебра. Лекция 6. Классы вычетов Умножение десятичных дробей
Умножение десятичных дробей Уравнения, сводящиеся к квадратным уравнениям
Уравнения, сводящиеся к квадратным уравнениям Урок математики Решение задач на движение
Урок математики Решение задач на движение  Упрощение выражений. 5 класс
Упрощение выражений. 5 класс Занимательная математика
Занимательная математика Средняя линия треугольника
Средняя линия треугольника Прямая. Луч. Отрезок. (2 класс)
Прямая. Луч. Отрезок. (2 класс)