Содержание
- 2. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПО КООРДИНАТАМ ( II рода) 1. Задача, приводящая к понятию криволинейного интеграла II рода
- 3. Разобьем кривую (ℓ) произвольным образом на n частей точками M0=L1, M1, …, Mn=L2 в направлении от
- 4. Сумму назовем интегральной суммой для функции P(x,y,z) по кривой (ℓ) по переменой x (соответствующей данному разбиению
- 5. Пусть Обозначают: где ΔMi–1Mi – длина дуги (Mi–1Mi) или
- 6. Аналогично определяются интегралы Сумму записывают в виде и называют криволинейным интегралом II рода (по координатам).
- 7. СВОЙСТВА КРИВОЛИНЕЙНОГО ИНТЕГРАЛА II РОДА Замечание: предполагаем, что все рассматриваемые в свойствах интегралы существуют. 1. Криволинейный
- 8. На плоскости положительным направлением обхода является направление против хода часовой стрелки. Криволинейный интеграл II рода по
- 9. 4. Постоянный множитель можно выносить за знак криволиней- ного интеграла II рода, т.е. 3. ФИЗИЧЕСКИЙ СМЫСЛ
- 10. 5. Криволинейный интеграл II рода от алгебраической суммы двух (конечного числа) функций равен алгебраической сумме криволинейных
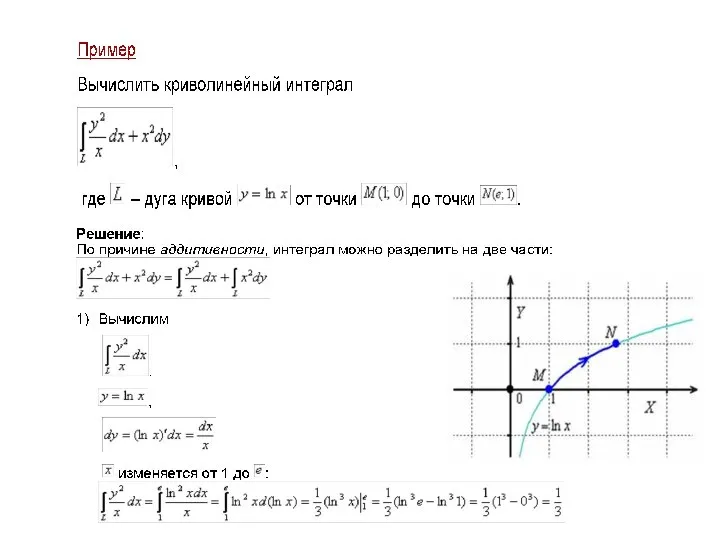
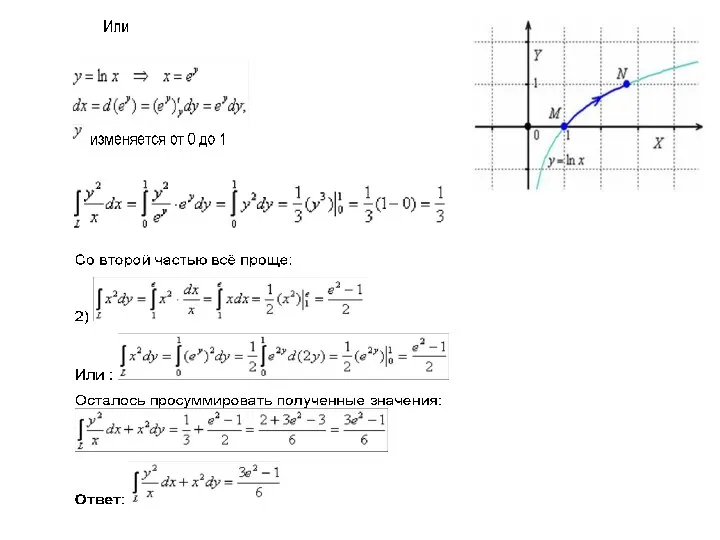
- 11. 3. Вычисление криволинейного интеграла II рода Пусть простая (не имеющая кратных точек) кривая (ℓ)=(L1L2) задана параметрическими
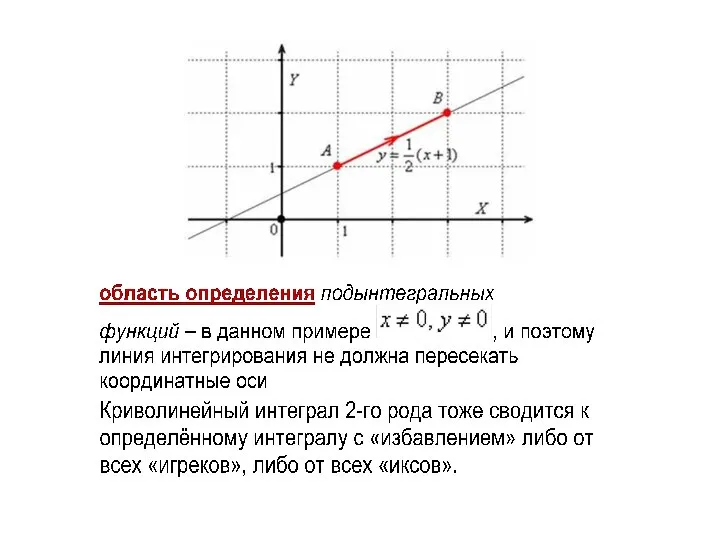
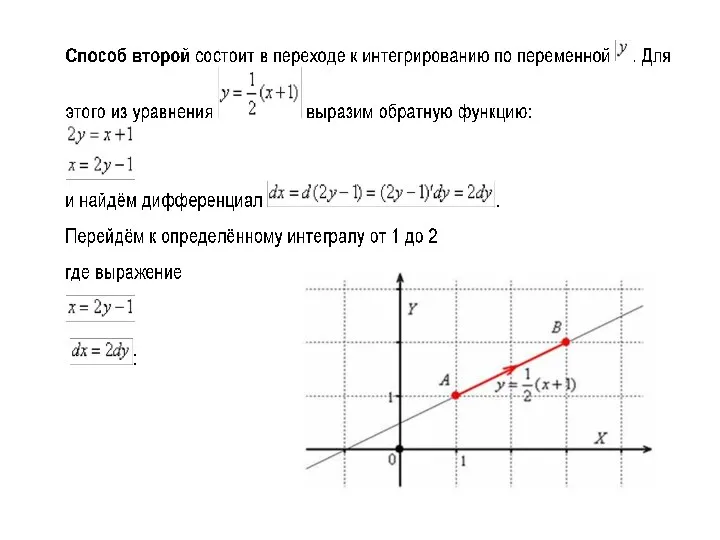
- 12. СЛЕДСТВИЕ 2. Если (ℓ) = (L1L2) – гладкая кривая в плоскости xOy , заданная уравнением y
- 13. криволинейный интеграл 2-го рода зависит от направления интегрирования, причём:
- 25. Скачать презентацию


















 Математический диктант
Математический диктант Решение тригонометрических уравнений различных типов
Решение тригонометрических уравнений различных типов Определители второго и третьего порядка
Определители второго и третьего порядка Зеркальная симметрия
Зеркальная симметрия История возникновения интегралов. Историческая справка
История возникновения интегралов. Историческая справка Элементы математической логики. Интегральное исчисление функций одной переменной и его приложения
Элементы математической логики. Интегральное исчисление функций одной переменной и его приложения Метрологическое обеспечение производства по переработке мясных продуктов
Метрологическое обеспечение производства по переработке мясных продуктов Закрепление знаний, умений и навыков решения задач на проценты
Закрепление знаний, умений и навыков решения задач на проценты Порядковые числительные
Порядковые числительные Презентация по математике "Числа - великаны вокруг и внутри нас" - скачать
Презентация по математике "Числа - великаны вокруг и внутри нас" - скачать  Взаимно обратные числа
Взаимно обратные числа Презентация по математике "Архимед" - скачать
Презентация по математике "Архимед" - скачать  Прямоугольный треугольник. Признаки равенства прямоугольных треугольников
Прямоугольный треугольник. Признаки равенства прямоугольных треугольников График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Тригонометрические формулы. 10 класс
Тригонометрические формулы. 10 класс Математика. Часть 2
Математика. Часть 2 Число и цифра 7. Состав числа 7
Число и цифра 7. Состав числа 7 Математическое обеспечение САПР
Математическое обеспечение САПР Игра "Счастливый случай". Внеклассное мероприятие по математике
Игра "Счастливый случай". Внеклассное мероприятие по математике Подготовка к ВПР. Математика 5 класс
Подготовка к ВПР. Математика 5 класс Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Разложение квадратного трехчлена на множители при преобразовании выражений
Разложение квадратного трехчлена на множители при преобразовании выражений Логарифмы и их свойства
Логарифмы и их свойства Парная линейная регрессионная модель
Парная линейная регрессионная модель Аттестационная работа. Программа курса «Математический калейдоскоп»
Аттестационная работа. Программа курса «Математический калейдоскоп» Путешествие к острову натуральных чисел. 5 класс
Путешествие к острову натуральных чисел. 5 класс Успешные люди – люди, которые в полной мере используют свой интеллект
Успешные люди – люди, которые в полной мере используют свой интеллект Аттестационная работа. Образовательная программа внеурочной деятельности обучающихся «Наглядная геометрия» в 5-6 классах»
Аттестационная работа. Образовательная программа внеурочной деятельности обучающихся «Наглядная геометрия» в 5-6 классах»