Квадратные уравнения. 8 класс

Содержание

1. Определение квадратного уравнения.
2. Виды квадратных уравнений:
а) полные квадратные уравнения;
приведенные квадратные

Определение

Квадратным уравнением называется уравнение вида ax2 + bx + c = 0, где x – переменная, а a,b и c -некоторые

Пример.

Назовите в квадратном уравнении коэффициенты:
а) 5х2-9х+4=0.
б) -х2+5х=0.
Решение:
а) a=5, b=-9, c=4.
б)

Реши самостоятельно.

Назовите в квадратном уравнении коэффициенты:
а) х2+3х-10=0.
б) 6х2-30=0.
в) 9х2=0.

Виды квадратных уравнений

Полным квадратным уравнением называют такое, все коэффициенты которого отличны от

Полное квадратное уравнение

 ax2 + bx + c = 0, (a, b, c ≠0)
Число D = b2 − 4ac - дискриминант.
По знаку дискриминанта можно

Пример

Сколько корней имеют квадратные уравнения:
1) x2 − 8x + 12 = 0;
2) 5x2 + 3x + 7 = 0;
3) x2 − 6x + 9 = 0.

Решение

Выпишем коэффициенты и найдем дискриминант: 1) x2 − 8x + 12 = 0;
a = 1, b = −8, c = 12; D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
D>0, поэтому уравнение имеет

2) 5x2 + 3x + 7 = 0;
a = 5; b = 3; c = 7; D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
D<0, корней нет.
3) x2 − 6x + 9 = 0.
a = 1; b = −6; c = 9; D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
D=0 — один корень.

Реши самостоятельно.

Сколько корней имеют квадратные уравнения:
1) 2x2 + 3x + 1 = 0;
2) 9x2 + 6x + 1 = 0;
3) 3x2 +x + 2 = 0.
4) x2 + 5x -6 = 0;

Формула корней квадратного уравнения
Когда D > 0, корни можно найти по формулам:
Когда D = 0, можно

Пример

Решить квадратные уравнения:
2x2 − x − 5 = 0;
15 − 2x + x2 = 0;
3) x2 + 12x + 36 = 0.

Решение

1) 2x2 − x − 5 = 0; :  a = 2; b = −1; c = −5; D = (−1)2 − 4 · 2 · (−5) = 41.
D > 0 - уравнение имеет два корня. Найдем их:

2) 15 − 2x + x2 = 0 
a = 1; b = −2; c = 15; D = (−2)2 − 4 · 1 · 15 = -56.
D < 0 , корней нет.
3) x2 + 12x + 36 = 0
a = 1; b = 12; c = 36; D = 122 − 4 · 1 · 36 = 0.
D = 0 , уравнение имеет один

Реши самостоятельно.

Решить квадратные уравнения:
3x2 − 7x +4 = 0;
-y2 +3y -5  = 0;
3) 1-18p+81p2 = 0.

Формула корней квадратного уравнения при чётном коэффициенте b

Для уравнений вида ax2+2kx+c=0, то

Пример

Решить квадратные уравнения:
3x2 − 14x +16 = 0;
x2 + 2x  − 80    = 0;
3) y2 - 10y -25 = 0.

Решение

3x2 − 14x +16 = 0; 
a = 3; b = −14; c = 16; k=-7.
D1 = (−7)2 − 3 · 16 = 1.
D1 > 0 - уравнение имеет два корня. Найдем их:

2) x2 + 2x  − 80    = 0
a = 1; b = 2; c = -80; k=1.
D1 = 12 −  1 · (-80) = 81.
D1 > 0 , 2 корня.
3) y2 - 10y +25 = 0.
a = 1; b = -10;

Реши самостоятельно.

Решить квадратные уравнения:
8x2 − 14x +5 = 0;
4y2 +14y +1  = 0;
3) 80+32t+3t2 = 0.

Приведённые квадратные уравнения

Пусть дано приведенное квадратное
уравнение x2 +px +q = 0, тогда
D= p2 -4q
Также приведенное квадратное

Теорема Виета.

Сумма корней приведённого квадратного уравнения x2 +px +q = 0 равна второму коэффициенту с противоположным

Пример

Решить приведенное квадратное уравнение:
x2 -8x +12 = 0
Удобнее начинать подбор корней с произведения:
произведение корней положительное

Реши самостоятельно.

Найдите корни уравнения, используя теорему Виета.
x2 -15x -16 = 0

x2 -9x +20 = 0

x2 +x -56 = 0

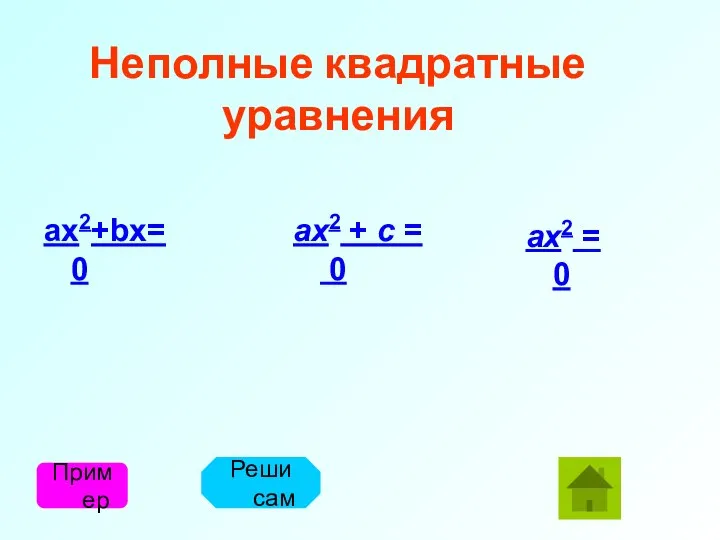
Неполные квадратные уравнения

Пример

Реши сам

ax2+bx=0

ax2 + c = 0

ax2 = 0

Уравнение ax2+bx=0 (c = 0, b  ≠ 0);

В левой части нужно разложить

Уравнение ax2 + c = 0, (b = 0; c ≠ 0)
Если , то уравнение имеет 2 корня:
Если

Уравнение ax2 = 0, (b = 0; c = 0)

Пример

Решить квадратные уравнения:
1) x2 − 7x = 0;
2) 5x2 + 30 = 0;
3) 4x2 − 9 = 0.

Решение

1)x2 − 7x = 0,
 x · (x − 7) = 0,
 x1 = 0; x2 = 7.
2) 5x2 + 30 = 0 ,
5x2 = −30,
 x2 = −6.
Корней нет, т.к. квадрат не может быть равен отрицательному

3) 4x2 − 9 = 0,
4x2 = 9,

Реши самостоятельно.

Решить квадратные уравнения:
1) 3x2 − 45x = 0;
2) 3x2 -2 = 0;
3) 6x2 +24 = 0.

Приемы устного решения квадратных уравнений
1 приём «коэффициентов»
2 приём «коэффициентов»
приём «переброски»

Пример

1 приём «коэффициентов»

Пусть дано квадратное
уравнение  ax2 + bx + c = 0, где a ≠ 0.
Если a + b +

2 приём «коэффициентов»

Пусть дано квадратное
уравнение  ax2 + bx + c = 0, где a ≠ 0.
2) Если b = a

Приём «переброски»

Пусть дано квадратное
уравнение  ax2 + bx + c = 0, где a ≠ 0.
Если а + b + c

Пример 1.

Прием 1
4+(-13)+9=0

Прием 2
4 + 7 = 11

Пример 2.

Решите уравнение:
Решаем по теореме Виета полученное уравнение,
и его корни 10

Реши самостоятельно.

ТЕСТ «КВАДРАТНЫЕ УРАВНЕНИЯ»

1. Какие из данных уравнений являются квадратными:
1)5х2-14х+17=0 2)-7х2-13х+8=0
3)-13х2+х3-1=0

2.Запишите квадратное уравнение, если его коэффициенты: а=2, b=3, с=4.
А. 3х2+2х+4=0;
Б. 4х2+2х+3=0;
В.

5.Запишите приведенное квадратное уравнение, имеющие кони 3 и -1.
А. х2-3х-2=0; Б. х2+3х-2=0;

ОТВЕТЫ.

1. Б
2. В
3. Б
4. В
5. В
6. А
7. В
8. -1 и
9. 2