Содержание
- 2. СЛАУ n-го порядка В векторной форме:
- 3. Здесь индексы α, β, ..., ω пробегают все возможные n! перестановок номеров 1, 2, ..., n;
- 4. Метод исключения Гаусса
- 5. Идея: последовательное исключение неизвестных, приводящее исходную систему к треугольному виду, в котором все коэффициенты ниже главной
- 6. Получим новую систему, в которой первое уравнение осталось неизменным, а остальные больше не содержат член с
- 7. При помощи второго уравнения исключаются коэффициенты при х2 из третьего, четвертого и последующих уравнений. Продолжая этот
- 8. На каждом шаге новые значения коэффициентов определяются через значения на предыдущем шаге согласно где m –
- 9. Обратный ход метода Гаусса состоит в последовательном вычислении xn, xn–1, ..., x1 по алгоритму Во время
- 10. Если элемент на главной диагонали мал, то эта строка умножается на большие числа, что приводит к
- 11. Метод прогонки
- 12. Модификация метода Гаусса, применяемая к системам с матрицей трехдиагонального типа (часто встречаются при решении краевых задач
- 13. В развернутом виде: b1x1 + c1x2 = d1; a2x1 + b2x2 + c2x3 = d2; a3x2
- 14. На этапе прямого хода каждое неизвестное xi выражается через xi+1 xi = Ai ⋅ xi+1 +
- 15. Расчет начинается с вычисления коэффициентов
- 16. На этапе обратного хода из последнего уравнения системы при i = n–1 Далее посредством прогоночных коэффициентов
- 17. Задание 1. Решить СЛАУ методом исключения Гаусса. Привести результат решения, а также вид матрицы системы и
- 18. Кому какая система? Для Гаусса
- 20. Скачать презентацию

















 Параллельный перенос
Параллельный перенос Решение задач. Повторение. 6 класс
Решение задач. Повторение. 6 класс Презентация Сравнение многозначных чисел
Презентация Сравнение многозначных чисел  ДОЛИ И ДРОБИ УМК «Школа 2000» Учебник Л. Г. Петерсон, 4 класс
ДОЛИ И ДРОБИ УМК «Школа 2000» Учебник Л. Г. Петерсон, 4 класс  Четырехугольники. Обобщающий урок. 8 класс
Четырехугольники. Обобщающий урок. 8 класс Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Расстояние от точки до фигуры
Расстояние от точки до фигуры Показательные уравнения и неравенства
Показательные уравнения и неравенства Длина окружности и площадь круга
Длина окружности и площадь круга Решение дробных рациональных уравнений. Алгебра 8 класс
Решение дробных рациональных уравнений. Алгебра 8 класс Степень с рациональным показателем
Степень с рациональным показателем Чтение слов на букву л.
Чтение слов на букву л. Вероятность события. Первый и второй вид задач
Вероятность события. Первый и второй вид задач Часть II. Случайные величины
Часть II. Случайные величины Итоговый тест по математике 2 класс
Итоговый тест по математике 2 класс Шепенко Г.Н.- учитель математики Берновской СОШ Старицкого р-на Тверской области
Шепенко Г.Н.- учитель математики Берновской СОШ Старицкого р-на Тверской области  Математика. Тест 5
Математика. Тест 5 Элементы комбинаторики
Элементы комбинаторики Эйлеровы графы. Гамильтоновы графы
Эйлеровы графы. Гамильтоновы графы Системы нечеткого вывода
Системы нечеткого вывода Окружность
Окружность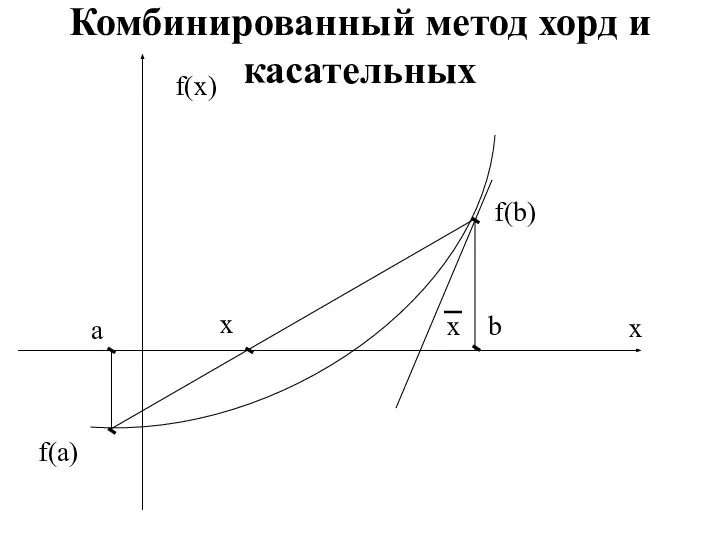 Комбинированный метод хорд и касательных
Комбинированный метод хорд и касательных Саннар. Чама саны приблизительные числительные
Саннар. Чама саны приблизительные числительные «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора» Иоганн Кеплер
«Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора» Иоганн Кеплер Углы, связанные с окружностью. Геометрия, 8 класс
Углы, связанные с окружностью. Геометрия, 8 класс Математическая викторина
Математическая викторина Выпуклые многоугольники
Выпуклые многоугольники Многоугольники в нашей жизни
Многоугольники в нашей жизни