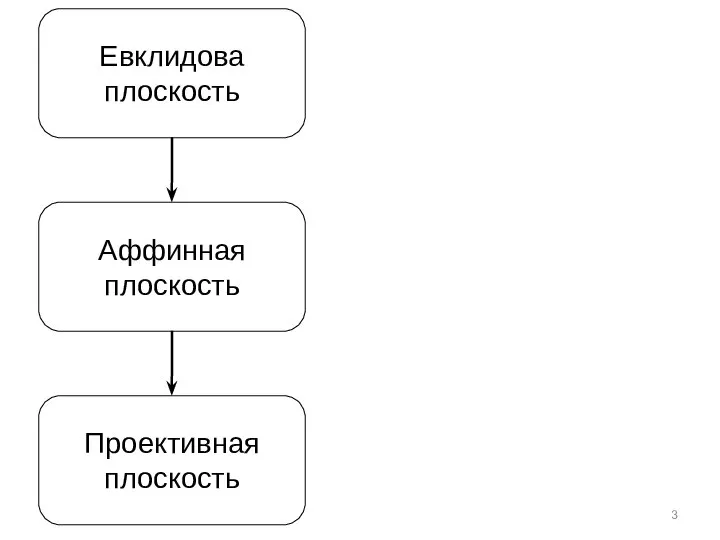
Содержание
- 2. 1. Некоторые воспоминания
- 5. Проективные свойства (инварианты)
- 6. Проективные свойства (инварианты) инцидентность коллинеарность конкуррентность
- 7. 2. Принцип двойственности
- 8. Взаимно-двойственные элементы точка прямая
- 9. Взаимно-двойственные элементы точка прямая Взаимно-двойственные операции провести прямую через точку отметить точку на прямой
- 10. Пример замены «точка ↔ прямая»
- 11. Пример замены «точка ↔ прямая»
- 12. Пример замены «точка ↔ прямая»
- 13. Пример замены «точка ↔ прямая»
- 14. Пример замены «точка ↔ прямая»
- 15. Принцип двойственности Из каждого проективного предложения относительно точек и прямых на плоскости может быть получено второе
- 16. Принцип двойственности Две фигуры взаимно двойственны, если одна может быть получена из другой посредством замены каждого
- 17. Принцип двойственности Две теоремы взаимно двойственны, если одна превращается в другую при замене каждого элемента и
- 18. Принцип двойственности Явление двойственности резко отличает проективную геометрию от элементарной (метрической), в которой никакой двойственности не
- 19. Принцип двойственности Явление двойственности резко отличает проективную геометрию от элементарной (метрической), в которой никакой двойственности не
- 20. Принцип двойственности Каждой верной теореме проективной геометрии сопоставляется двойственная ей, также верная теорема.
- 21. Принцип двойственности Каждой верной теореме проективной геометрии сопоставляется двойственная ей, также верная теорема. Следствие. Двойственную теорему
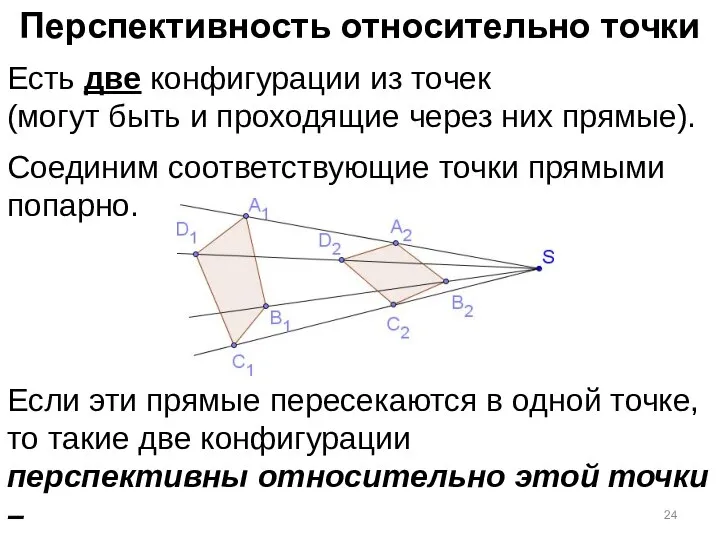
- 22. Перспективность относительно точки Есть две конфигурации из точек (могут быть и проходящие через них прямые).
- 23. Перспективность относительно точки Есть две конфигурации из точек (могут быть и проходящие через них прямые). Соединим
- 24. Перспективность относительно точки Есть две конфигурации из точек (могут быть и проходящие через них прямые). Соединим
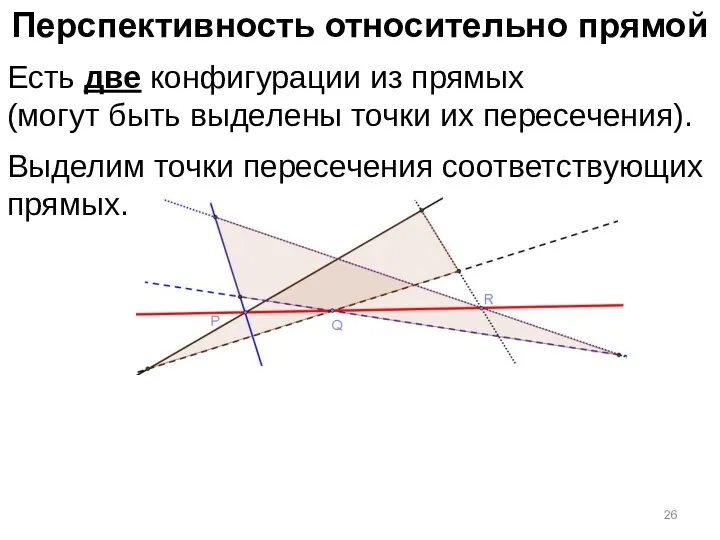
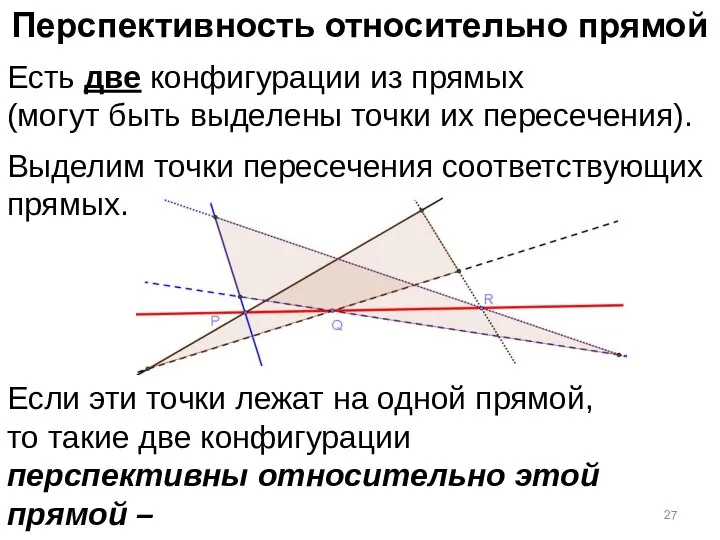
- 25. Перспективность относительно прямой Есть две конфигурации из прямых (могут быть выделены точки их пересечения).
- 26. Перспективность относительно прямой Есть две конфигурации из прямых (могут быть выделены точки их пересечения). Выделим точки
- 27. Перспективность относительно прямой Есть две конфигурации из прямых (могут быть выделены точки их пересечения). Выделим точки
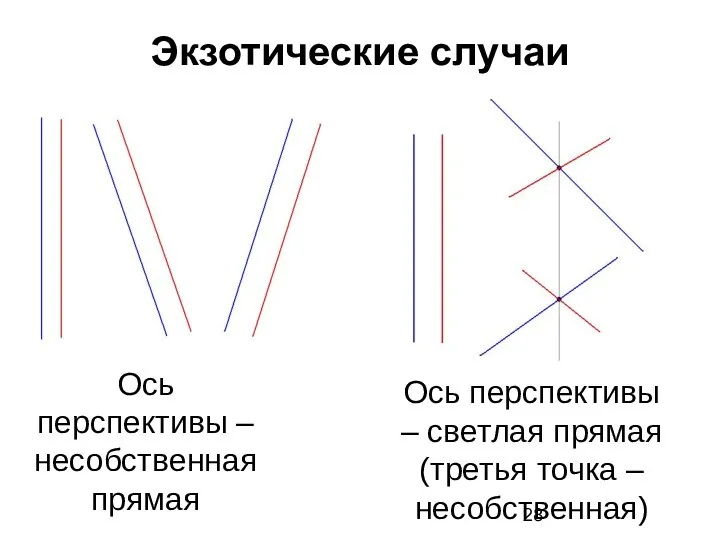
- 28. Экзотические случаи Ось перспективы – несобственная прямая Ось перспективы – светлая прямая (третья точка – несобственная)
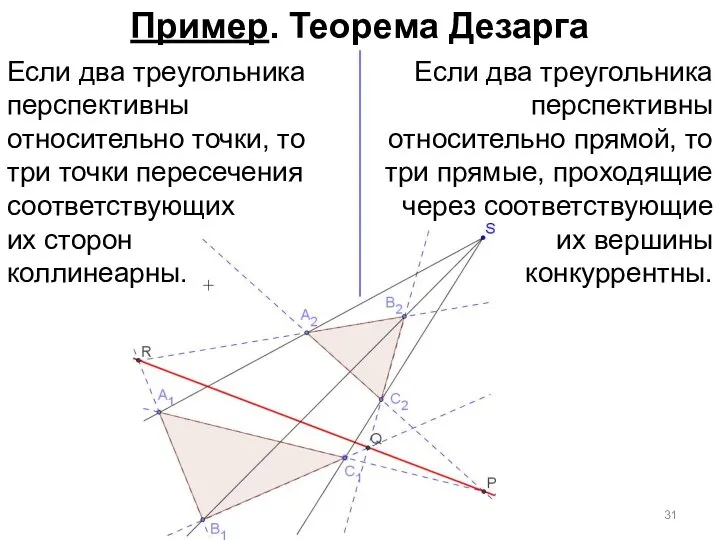
- 29. Пример. Теорема Дезарга
- 30. Пример. Теорема Дезарга
- 31. Пример. Теорема Дезарга
- 32. Пример. Теорема Дезарга
- 33. Пример. Теорема Дезарга
- 34. Вспомогательные теоремы
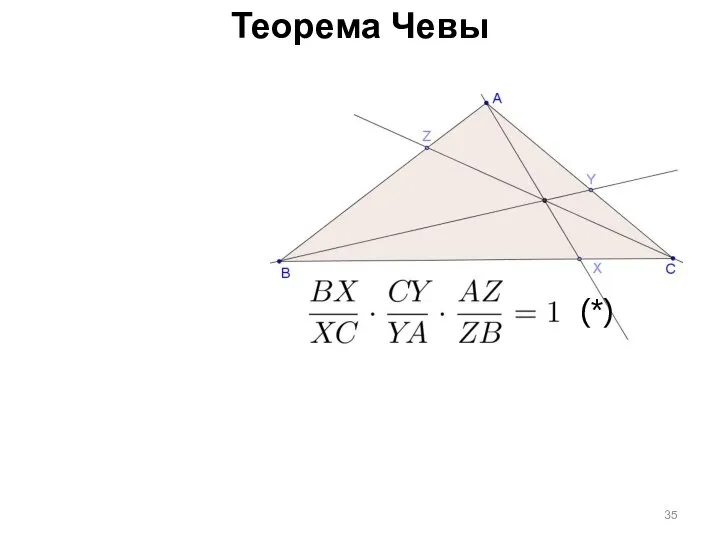
- 35. Теорема Чевы (*)
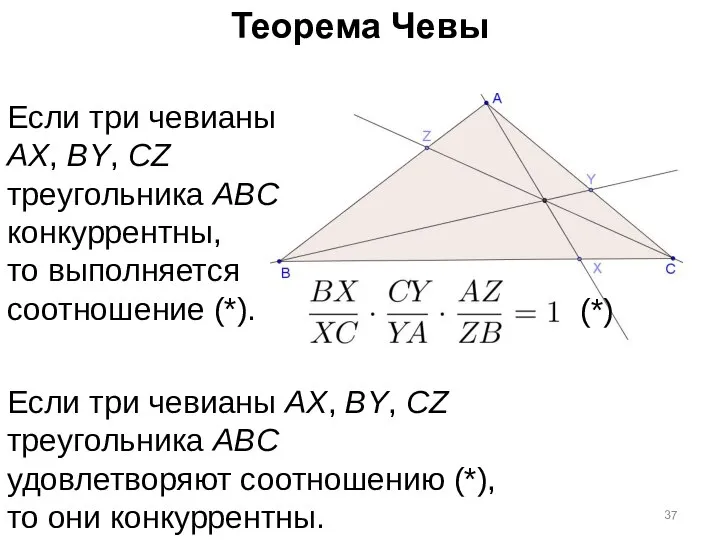
- 36. Теорема Чевы Если три чевианы AX, BY, CZ треугольника ABC конкуррентны, то выполняется соотношение (*). (*)
- 37. Теорема Чевы Если три чевианы AX, BY, CZ треугольника ABC конкуррентны, то выполняется соотношение (*). Если
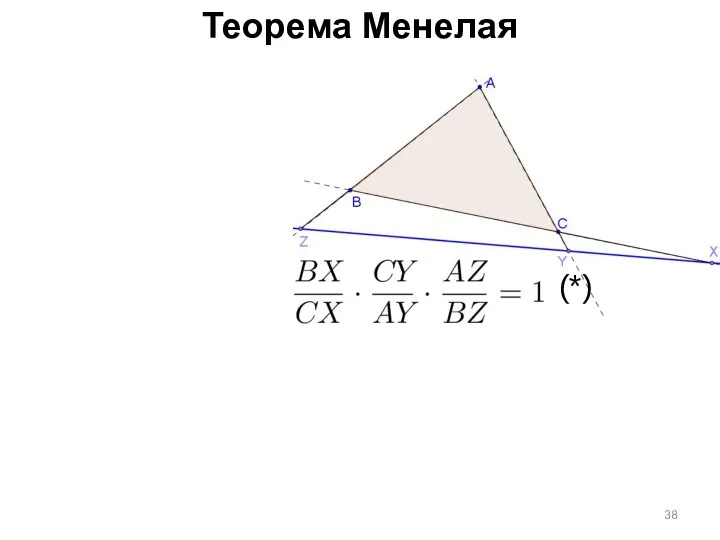
- 38. Теорема Менелая (*)
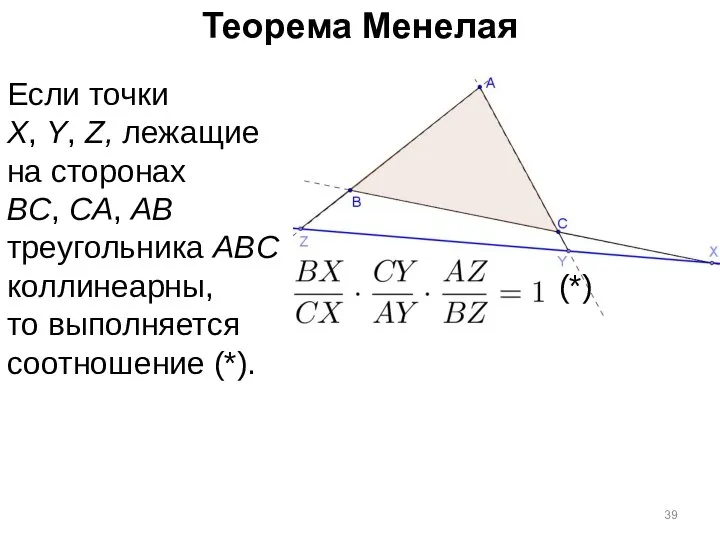
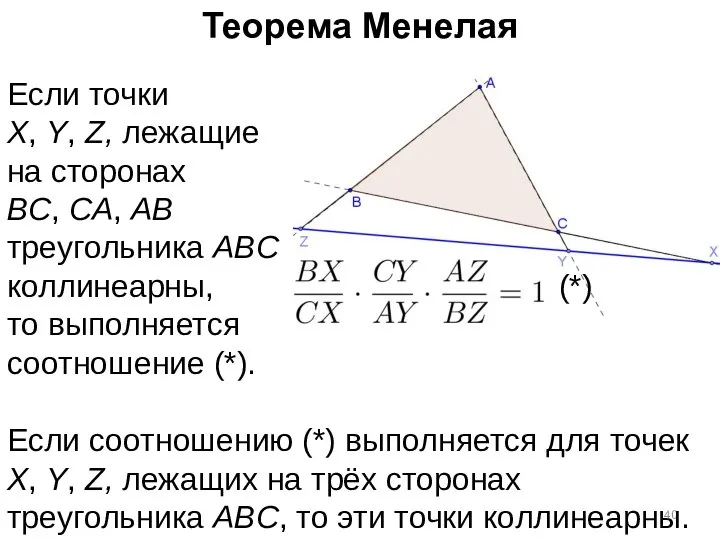
- 39. Теорема Менелая Если точки X, Y, Z, лежащие на сторонах BC, CA, AB треугольника ABC коллинеарны,
- 40. Теорема Менелая Если точки X, Y, Z, лежащие на сторонах BC, CA, AB треугольника ABC коллинеарны,
- 41. Резюме Теорема Чевы – критерий конкуррентности. Теорема Менелая – критерий коллинеарности.
- 42. Домашнее задание Доказать теоремы Чевы и Менелая (прямую и обратную).
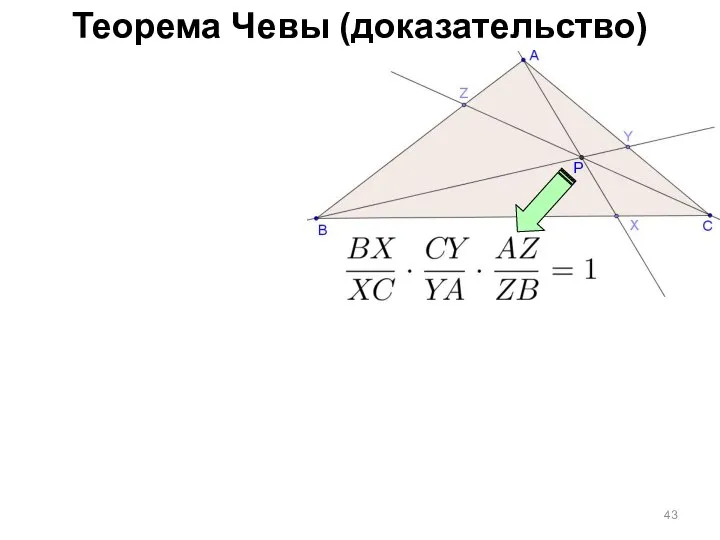
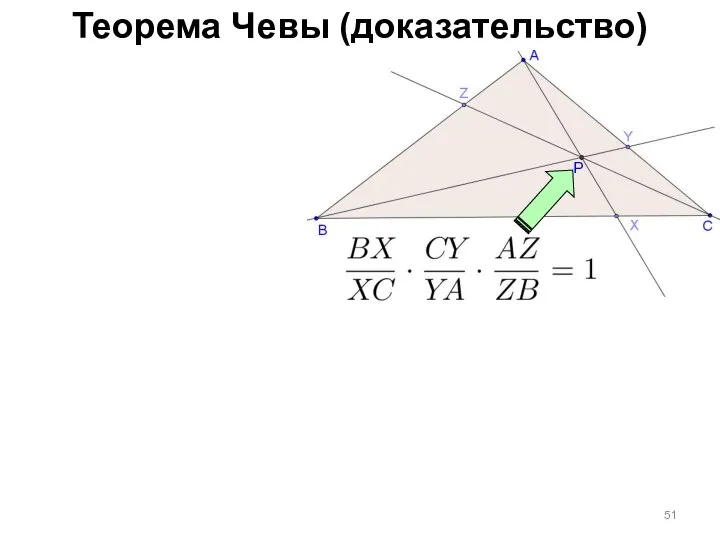
- 43. Теорема Чевы (доказательство)
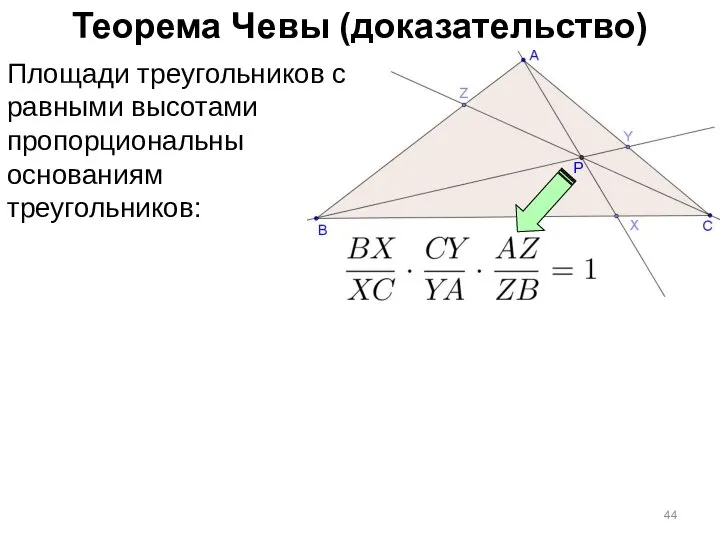
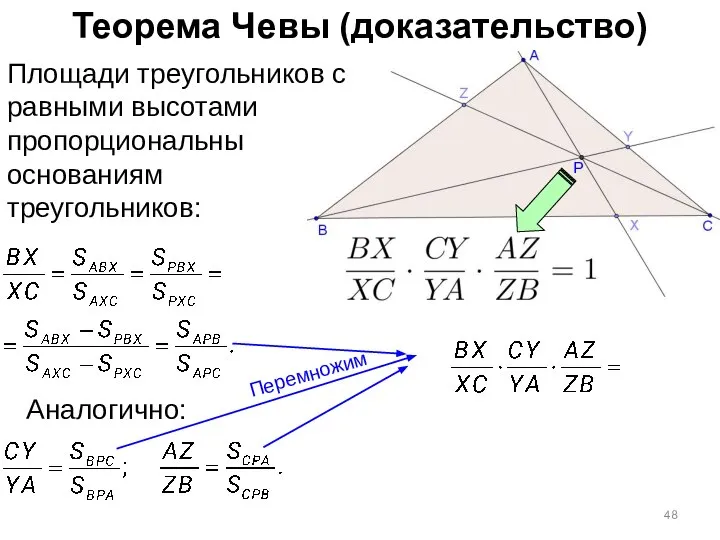
- 44. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников:
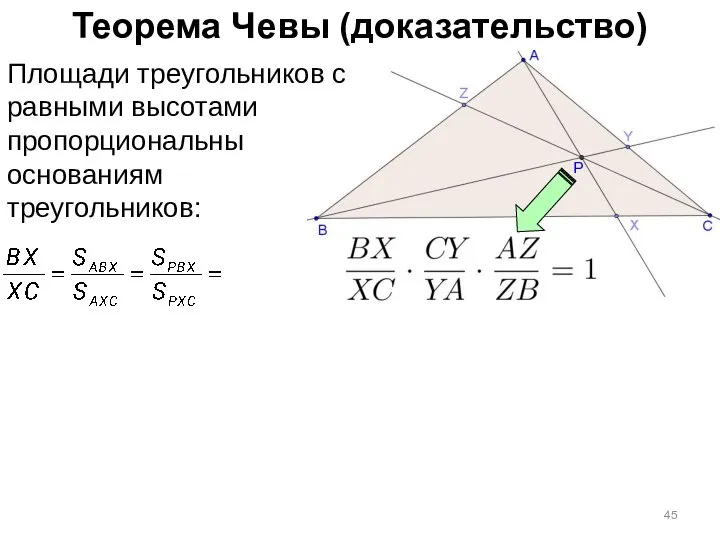
- 45. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников:
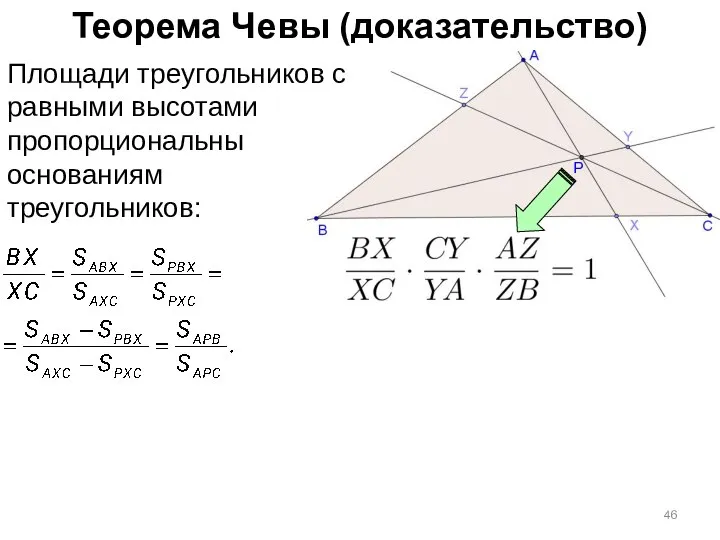
- 46. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников:
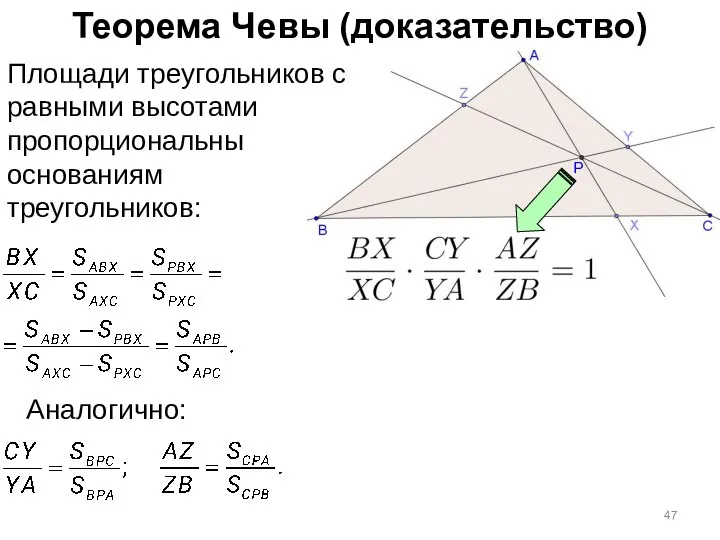
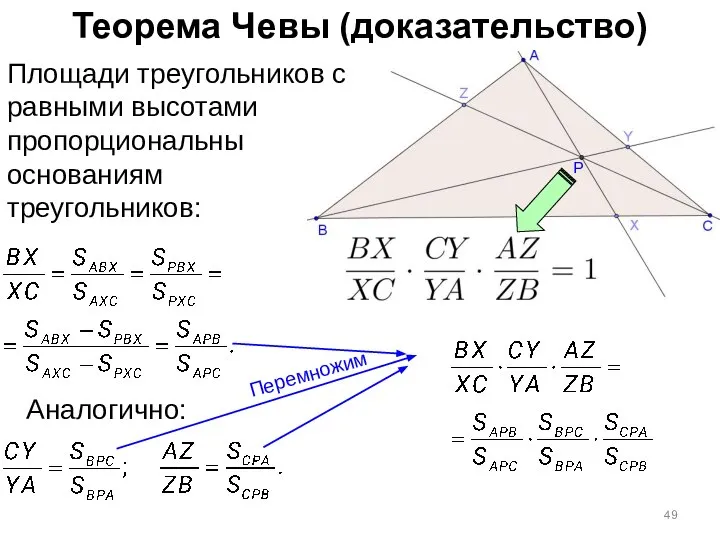
- 47. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников: Аналогично:
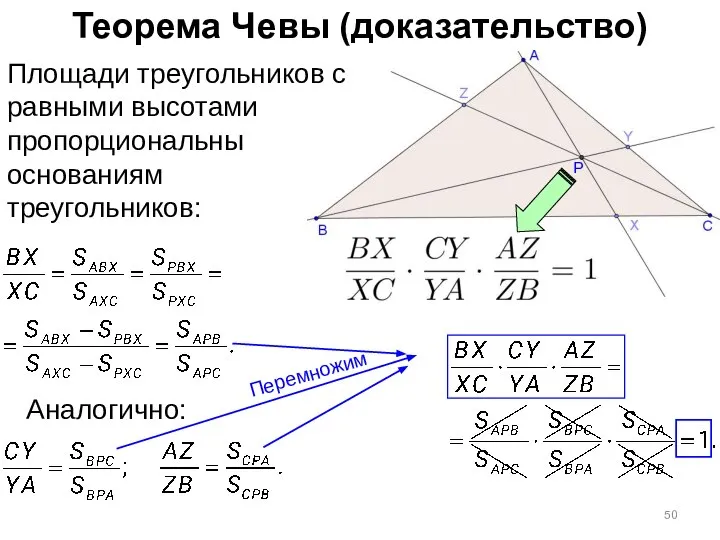
- 48. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников: Аналогично: Перемножим
- 49. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников: Аналогично: Перемножим
- 50. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников: Аналогично: Перемножим
- 51. Теорема Чевы (доказательство) P
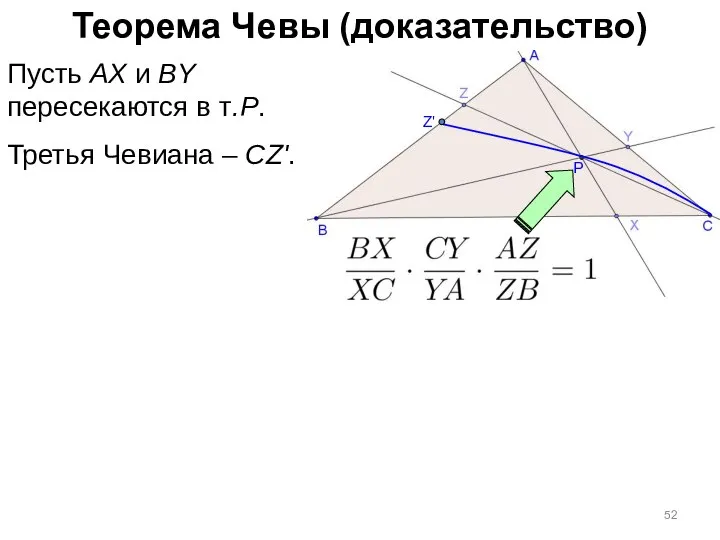
- 52. Теорема Чевы (доказательство) P Пусть AX и BY пересекаются в т.P. Третья Чевиана – CZ'. Z'
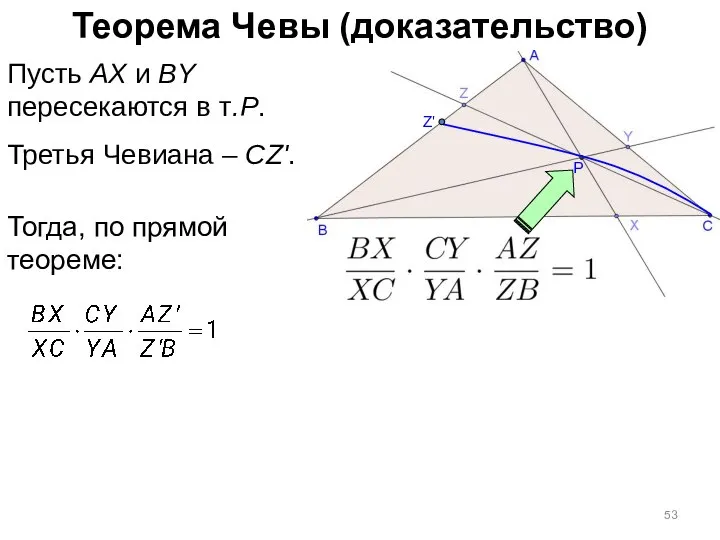
- 53. Теорема Чевы (доказательство) P Пусть AX и BY пересекаются в т.P. Третья Чевиана – CZ'. Z'
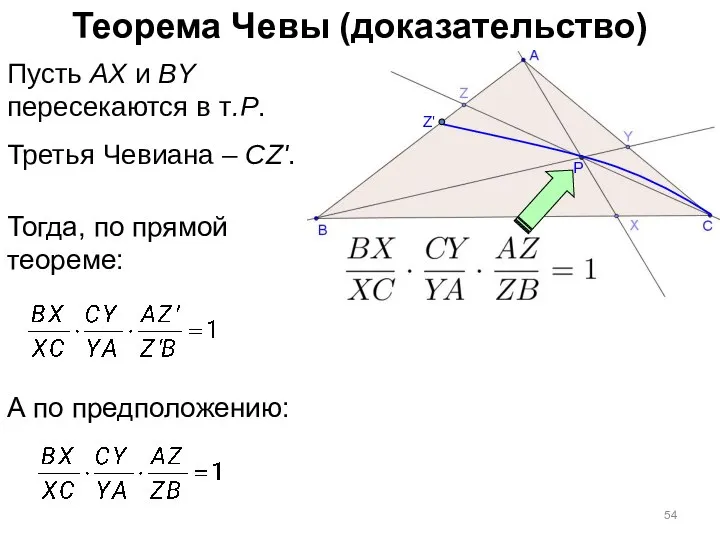
- 54. Теорема Чевы (доказательство) P Пусть AX и BY пересекаются в т.P. Третья Чевиана – CZ'. Z'
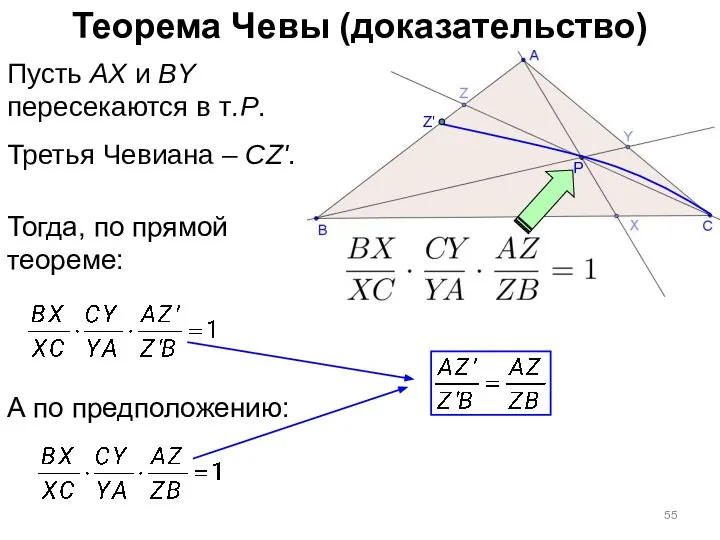
- 55. Теорема Чевы (доказательство) P Пусть AX и BY пересекаются в т.P. Третья Чевиана – CZ'. Z'
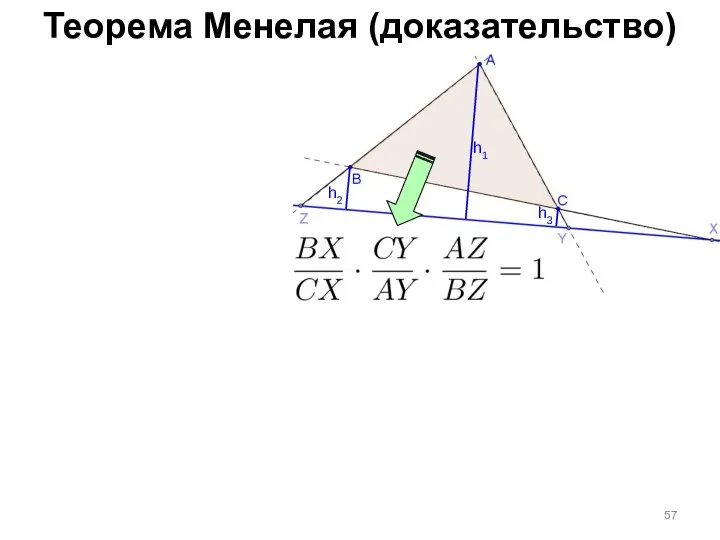
- 56. Теорема Менелая (доказательство)
- 57. Теорема Менелая (доказательство) h1 h3 h2
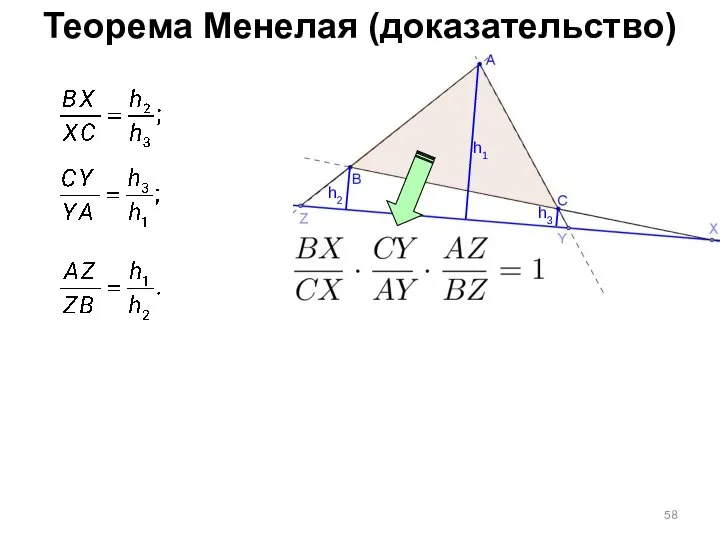
- 58. Теорема Менелая (доказательство) h1 h3 h2
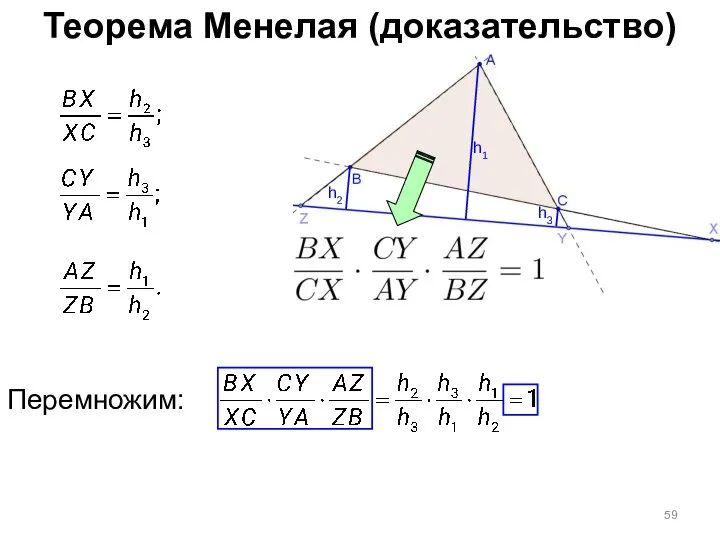
- 59. Теорема Менелая (доказательство) h1 h3 h2 Перемножим:
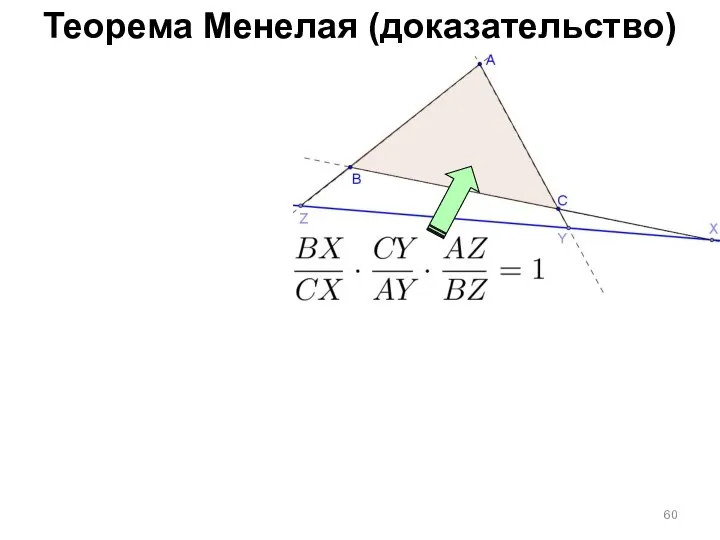
- 60. Теорема Менелая (доказательство)
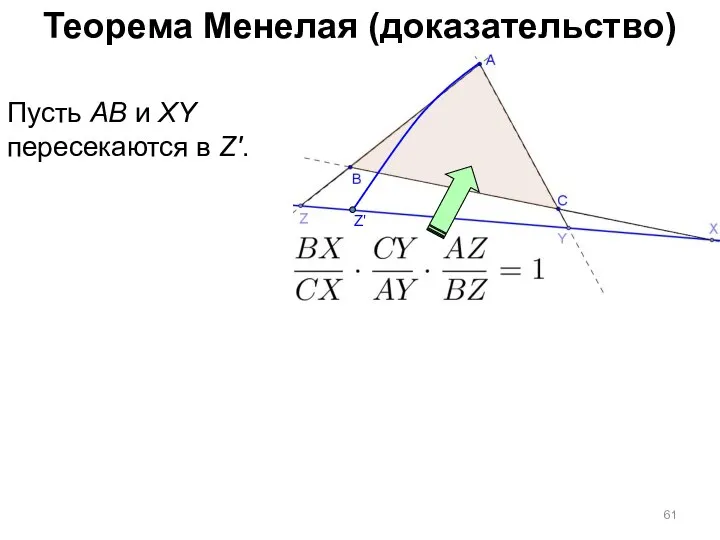
- 61. Теорема Менелая (доказательство) Пусть AB и XY пересекаются в Z'. Z'
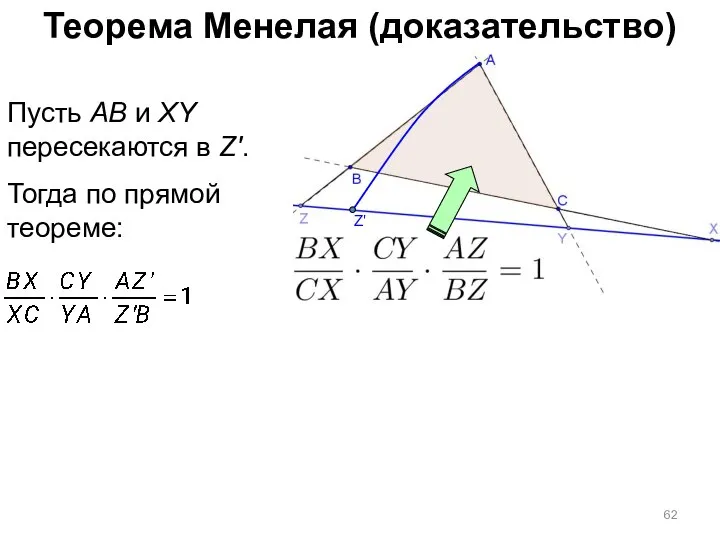
- 62. Теорема Менелая (доказательство) Пусть AB и XY пересекаются в Z'. Тогда по прямой теореме: Z'
- 63. Теорема Менелая (доказательство) Пусть AB и XY пересекаются в Z'. Тогда по прямой теореме: А по
- 65. Скачать презентацию
































 Геометрический смысл производной
Геометрический смысл производной История возникновения счёта, появление цифр и систем счисления
История возникновения счёта, появление цифр и систем счисления Арифметический диктант. Математика
Арифметический диктант. Математика Презентация на тему Путешествие в сказочное математическое королевство
Презентация на тему Путешествие в сказочное математическое королевство Геометрические фигуры
Геометрические фигуры Функции. Пределы функций
Функции. Пределы функций Отрезок. Измерение отрезков. Решение задач. Геометрия 7 класс
Отрезок. Измерение отрезков. Решение задач. Геометрия 7 класс Геометрические фигуры
Геометрические фигуры Метод главных элементов для решения системы линейных уравнений
Метод главных элементов для решения системы линейных уравнений Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Решение неравенств с одной переменной. Алгебра 8 класс
Решение неравенств с одной переменной. Алгебра 8 класс Огюстен Луи Коши (1789-1857)
Огюстен Луи Коши (1789-1857) Повторение пройденного Что узнали.чему научились
Повторение пройденного Что узнали.чему научились Отношение двух чисел
Отношение двух чисел Умножение суммы на число. (2 класс)
Умножение суммы на число. (2 класс) Презентация на тему Закон распределения случайной дискретной величины
Презентация на тему Закон распределения случайной дискретной величины Математические методы прогноза и восстановления зависимостей
Математические методы прогноза и восстановления зависимостей Математические понятия
Математические понятия Математика 4 класс
Математика 4 класс Формулы сокращенного умножения
Формулы сокращенного умножения Презентация по математике "Вычисление площадей с помощью интегралов" - скачать
Презентация по математике "Вычисление площадей с помощью интегралов" - скачать  Применение интеграла в физике и геометрии
Применение интеграла в физике и геометрии Криптографические методы защиты информации. Односторонние функции и система Диффи-Хеллмана. (Лекция 2)
Криптографические методы защиты информации. Односторонние функции и система Диффи-Хеллмана. (Лекция 2) Практическое применение интегралов в различных областях
Практическое применение интегралов в различных областях Функция y = cos x Ее свойства и график
Функция y = cos x Ее свойства и график  Буквенная запись свойств сложения и вычитания
Буквенная запись свойств сложения и вычитания Моделирование и анализ стохастических процессов на основе их локальных характеристик
Моделирование и анализ стохастических процессов на основе их локальных характеристик Множества
Множества