Содержание
- 2. Асимптотическое разложение в окрестности точки x0
- 3. При x0→∞ достаточно часто в качестве ϕ(x) выбираются обратные степени x:
- 4. Замечание. Асимптотический ряд, вообще говоря, не сходится. для достаточно гладких f( t ) и ϕ( t
- 5. Формула Лапласа Обобщим этот результат на случай интегралов от аналитических ФКП.
- 7. Max. вклад в интеграл даст тот участок C, на котором u( x, y ) достигает глобального
- 9. Δu=0, z∈g', и в силу принципа max. гармонической функции, max u|∂g > u(x , y)|(x,y)∈g'=> хотя
- 10. => Через z0∈С проходят другие направления на которых u( x, y ) возрастает от значения u(
- 11. Max. вклад в интеграл будет давать участок интегрирования в окрестности точки z0, если на нем u(
- 12. Участок С, проходящий через z0 можно направить по направлению наибыстрейшего спуска на поверхности u( x ,
- 13. Но ∇u∇v = ux vx + uy vy=0 ( условия Коши-Римана ). => Направление наибыстрейшего спуска-
- 14. Max. вклад в интеграл дает интегрирование по участку С, проходящему через z0 и совпадающему c v
- 15. z0- точка глобального max. => => f ‘ ( z0 ) = 0 (производная не зависит
- 16. Найдем направление наибыстрейшего спуска.
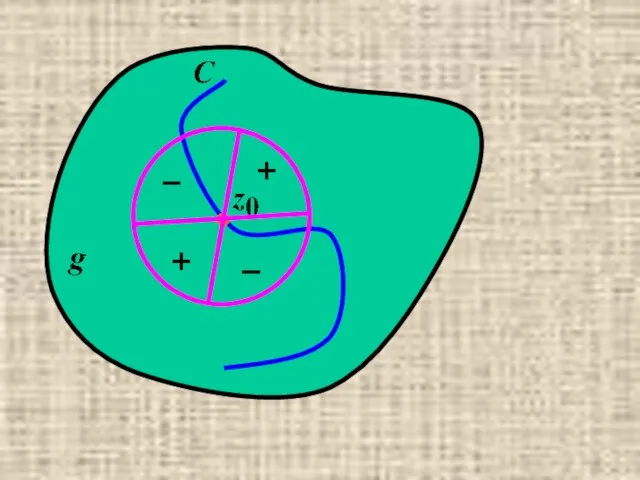
- 17. При 0 ≤ θ ≤ 2 π cos(ψ+2θ)=0 4 раза => окрестность точки z0 разбивается на
- 19. Направление наибыстрейшего спуска определяется условием cos(ψ+2θ) = -1 => ψ+2θ0=π; θ0=(π-ψ)/2, где f ’’ (z0)=2keiψ, ψ=
- 20. Вычислению первого члена асимптотики
- 21. Параметризуем контур интегрирования С :
- 22. Выполнены все условия применимости формулы Лапласа
- 28. Скачать презентацию











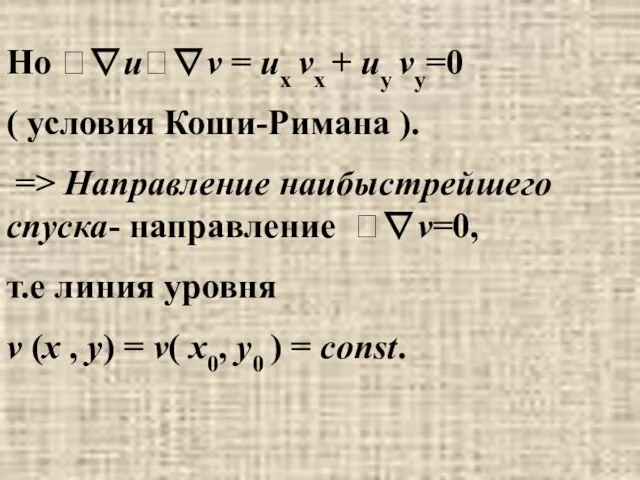

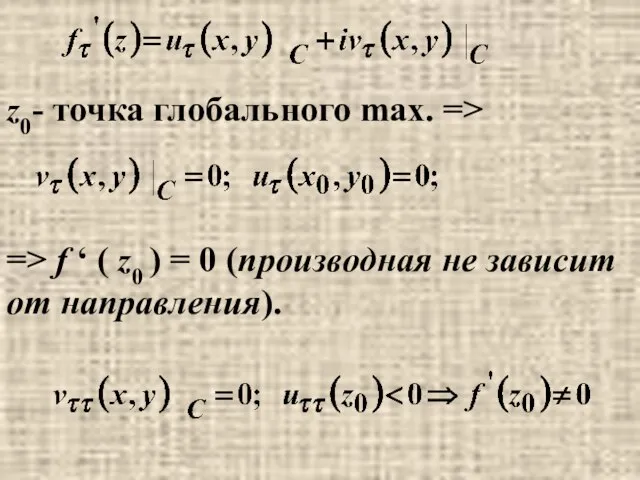
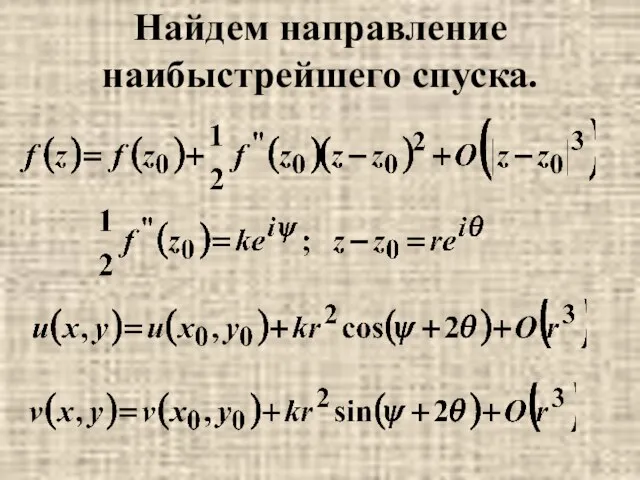


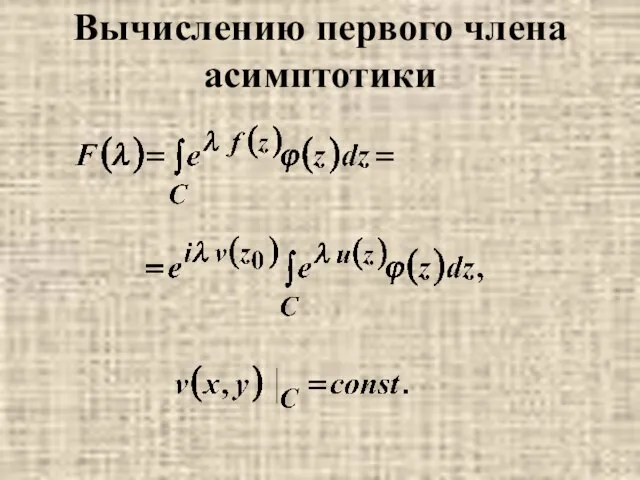
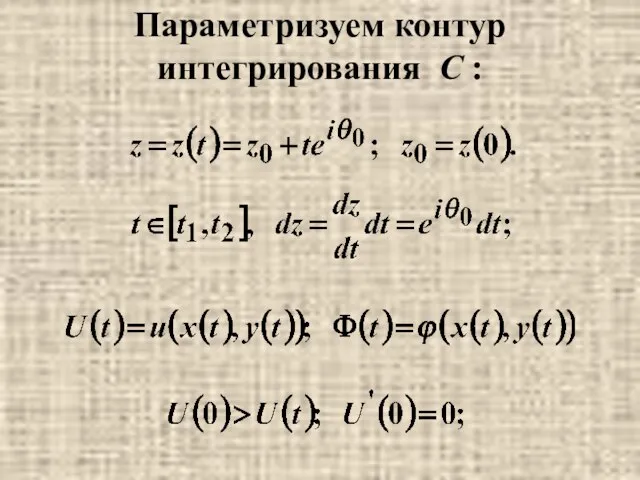




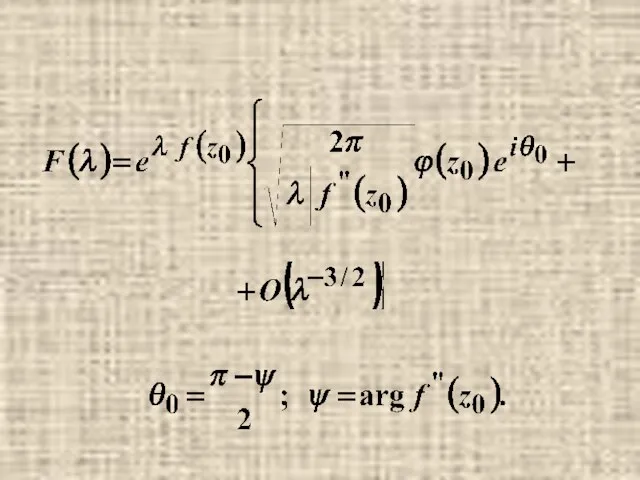
 Решение неравенств
Решение неравенств Презентация на тему Вычитание суммы из числа и числа из суммы
Презентация на тему Вычитание суммы из числа и числа из суммы  Аттестационная работа. Программа курса внеурочной деятельности по математике 5-6 класс Изучая математику, познавай мир
Аттестационная работа. Программа курса внеурочной деятельности по математике 5-6 класс Изучая математику, познавай мир Точность коэффициентов множественной регрессии
Точность коэффициентов множественной регрессии Разложение многочлена на множители с помощью комбинации различных приемов
Разложение многочлена на множители с помощью комбинации различных приемов Плоские фигуры в нашей жизни
Плоские фигуры в нашей жизни Действия с дробями. Задачи на движение
Действия с дробями. Задачи на движение Displaying data – shape of distributions. Week 3 (1)
Displaying data – shape of distributions. Week 3 (1) Комплексные числа
Комплексные числа Аттестационная работа. Методическая разработка элективного курса для 8 класса «Избранные вопросы математики»
Аттестационная работа. Методическая разработка элективного курса для 8 класса «Избранные вопросы математики» Микрокалькулятор
Микрокалькулятор Аттестационная работа. Образовательная программа внеурочной деятельности «Юный математик»
Аттестационная работа. Образовательная программа внеурочной деятельности «Юный математик» Урок математики в 6 «в» классе «Алгоритм решения задач на пропорции» Учитель: Лиманская Ю. И МОУ СОШ №11 _
Урок математики в 6 «в» классе «Алгоритм решения задач на пропорции» Учитель: Лиманская Ю. И МОУ СОШ №11 _ Предельные величины, эластичности
Предельные величины, эластичности Приемы решения целых уравнений
Приемы решения целых уравнений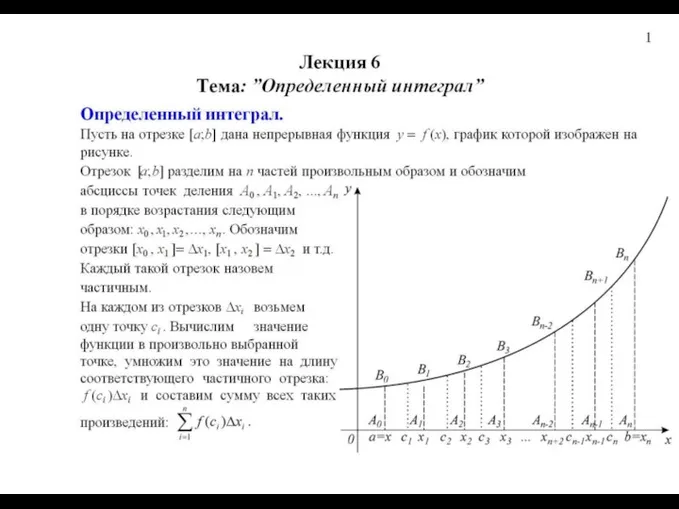 Лекция 6. Определенный интеграл
Лекция 6. Определенный интеграл Действия с десятичными дробями
Действия с десятичными дробями Математика
Математика Умножение дробей. Урок-игра. 6 класс
Умножение дробей. Урок-игра. 6 класс Координатная прямая
Координатная прямая Считаем со смешариками. Тренажер «Сложенеие и вычитание в пределах 10».Технологический прием «Анимированная сорбонка»
Считаем со смешариками. Тренажер «Сложенеие и вычитание в пределах 10».Технологический прием «Анимированная сорбонка» Оптимізаційні методи та моделі. Симплекс-метод розв'язання задач лінійної оптимізації. (Тема 4)
Оптимізаційні методи та моделі. Симплекс-метод розв'язання задач лінійної оптимізації. (Тема 4) Нестандартные способы математических вычислений
Нестандартные способы математических вычислений Решение рациональных неравенств 9 класс Подготовила: учитель математики МОУ сош №30 имени А.И.Колдунова Кутоманова Е.М. 2010-2011 уч
Решение рациональных неравенств 9 класс Подготовила: учитель математики МОУ сош №30 имени А.И.Колдунова Кутоманова Е.М. 2010-2011 уч Графический диктант. Математика. 5 класс
Графический диктант. Математика. 5 класс Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Решение задач. Площади поверхности
Решение задач. Площади поверхности Угол между векторами. Скалярное произведение векторов
Угол между векторами. Скалярное произведение векторов