Линейная алгебра

Литература

В.Л. Клюшин «Высшая математика для экономистов» (учебное пособие)
В.Л. Клюшин «Высшая математика

Понятие матрицы

Определение. Числовая таблица с m строками и n столбцами называется

Общий вид матрицы

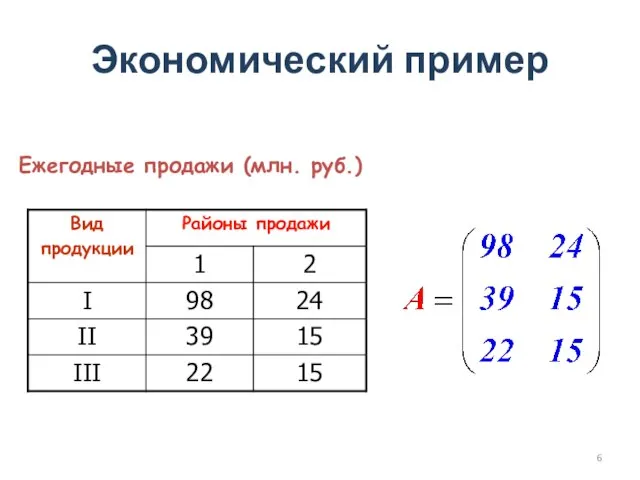
Экономический пример

Ежегодные продажи (млн. руб.)

Операции над матрицами (алгебра матриц)

Сложение и вычитание матриц

… производится поэлементно

Умножение матрицы на число

.

Умножение строки на столбец

.

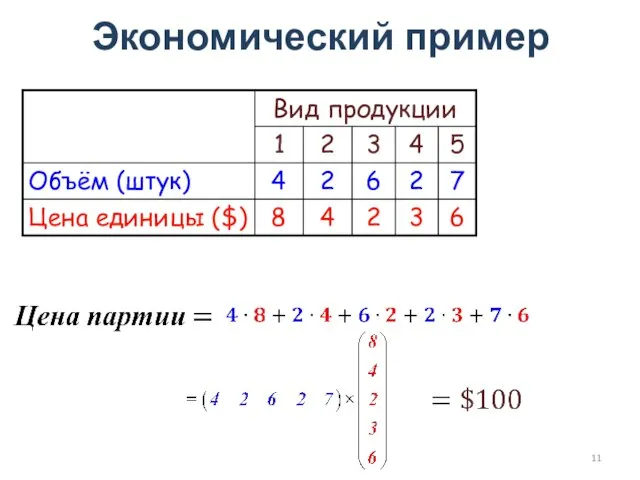
Экономический пример

Умножение строки на столбец

Пример. Умножить каждую строку матрицы A на каждый

Умножение матрицы на матрицу

Пример

.

Результат умножения матриц содержит столько же строк как первый сомножитель и

Связь алгебраических операций

≠

Транспонирование матриц

При транспонировании меняются местами строки и столбцы исходной матрицы. (Первая

Свойства операций над матрицами

Специальные виды матриц

Строка
Столбец
Квадратная
Диагональная
Нулевая
Верхнетреугольная
Нижнетреугольная

Пример

Определить типы следующих матриц (выбрать из строка, столбец, квадратная, диагональная, нулевая,

Определители квадратных матриц

Матрица 1-го порядка – таблица, состоящая из од-ного числа

Числовой пример

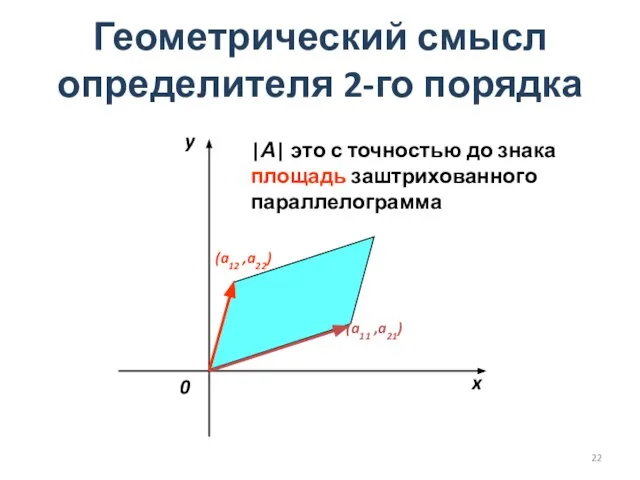
Геометрический смысл определителя 2-го порядка

|А| это с точностью до знака площадь

Решить систему уравнений:

Решить систему уравнений:

.

Решить систему уравнений:

Решить систему уравнений

Теорема Крамера

.

Пример

Разложение определителя по элементам строки или столбца

Разложение определителя по элементам строки или столбца

Пример
Для матрицы

Пример

.

Пример

Разложение определителя по элементам строки или столбца

Разложение определителя по элементам строки или столбца
Для матрицы

Разложение определителя по элементам строки или столбца

Теорема Лапласа. Определитель матрицы равен

Разложение определителя по элементам строки или столбца

Свойства определителей

Определитель не меняется при транспонировании:
Пример:

Свойства определителей

Определитель меняет знак при перестановки любых двух строк или любых

Свойства определителей

3. Общий множитель элементов какой-либо строки или столбца можно вынести

Свойства определителей

4. Определитель матрицы, содержащий строку или столбец, целиком состоящий из

Свойства определителей

5. Определитель матрицы, содержащий равные или пропорциональные строку и столбец,

Свойства определителей

Свойства определителей

Пример.

Свойства определителей

Определитель не изменится, если к элементам некоторой строки (столбца) прибавить

Пример

Свойства определителей

Определитель верхнетреугольной матрицы равен произведению диагональных элементов.
Пример:

Свойства определителей

(Теорема Лапласа.) Определитель равен сумме произведений элементов любой строки (столбца)

Свойства определителей

Если является единственным ненуле-вым элементом в своей строке или столбце,

Свойства определителей

Определитель произведения матриц равен произведению определителей:

Обратная матрица

Обратная матрица

Вопрос: существует ли аналог числа 1 и аналог обратного числа

Обратная матрица

Квадратная матрица называется диагональной, если все её элементы вне главной

Обратная матрица

Обратная матрица

Обратная матрица

Обратная матрица

Пример: так как
и

Обратная матрица

Теорема. Обратная матрица существует только для невырожденной квадратной матрицы.
Пример:

Обратная матрица второго порядка
Теорема.

Нахождение обратной матрицы методом присоединённой матрицы

Нахождение обратной матрицы методом присоединённой матрицы

Итак,

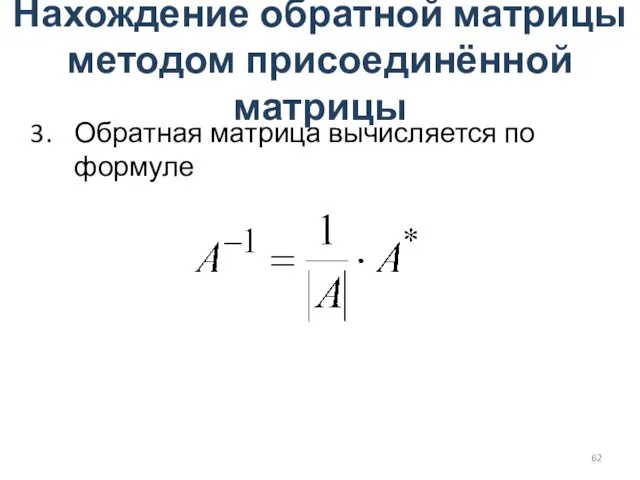
Нахождение обратной матрицы методом присоединённой матрицы

Обратная матрица вычисляется по формуле

Нахождение обратной матрицы методом присоединённой матрицы

Нахождение обратной матрицы методом присоединённой матрицы

2.

Нахождение обратной матрицы методом присоединённой матрицы

2. (продолжение)

Нахождение обратной матрицы методом присоединённой матрицы

(продолжение)

Нахождение обратной матрицы методом присоединённой матрицы

3.

Нахождение обратной матрицы методом присоединённой матрицы

Проверка:
Ответ:

Системы линейных уравнений

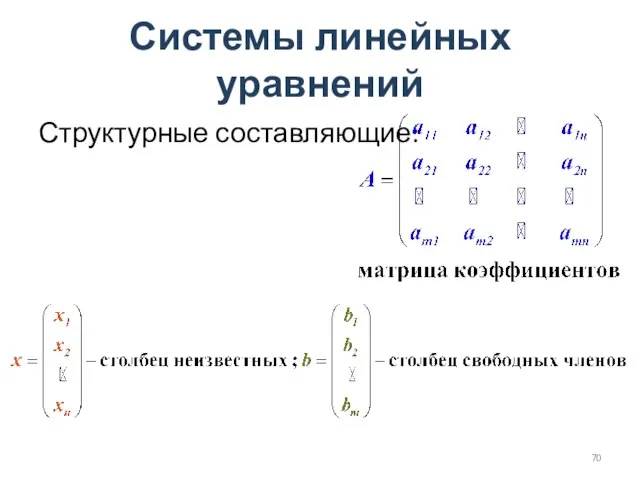
Системы линейных уравнений

Структурные составляющие:

Системы линейных уравнений

Пример:
Здесь m=3, n=3,

Системы линейных уравнений

Решением системы называется такой набор чисел (с1, с2,…, сn),

Системы линейных уравнений

Система называется определенной, если она имеет единственное решение; и

Метод обратной матрицы

Система уравнений
Равносильна матричному уравнению

Метод обратной матрицы

Метод обратной матрицы

В нашем случае