Содержание
- 3. 5. Теорема запаздывания.
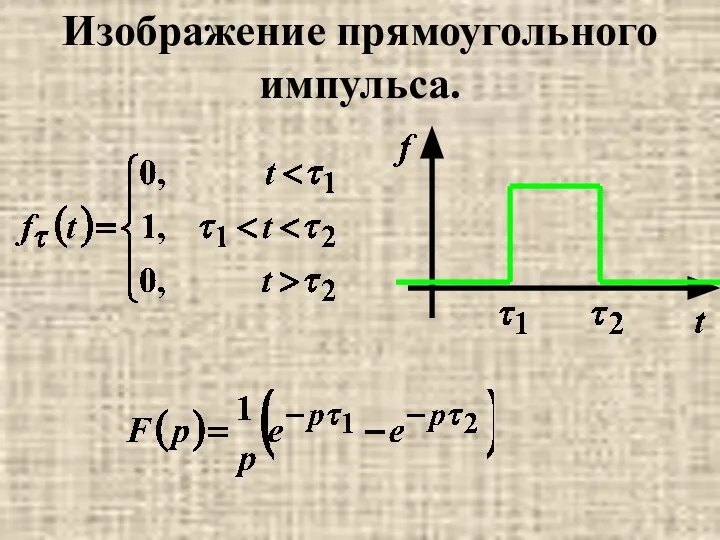
- 5. Изображение прямоугольного импульса.
- 6. 6. Изображение производной
- 7. (по частям)=
- 8. кусочно- непрерывная
- 10. 7. Изображение интеграла.
- 13. 8. Изображение свертки.
- 15. п.3. Решение задачи Коши для линейного обыкновенного дифференциального уравнения с постоянными коэффициентами операционным методом.
- 17. Пусть
- 22. Интеграл Дюгамеля.
- 23. п.4. Теорема Меллина. Пусть и (равномерно относительно аргумента) (равномерно ограничен по x )
- 24. Тогда
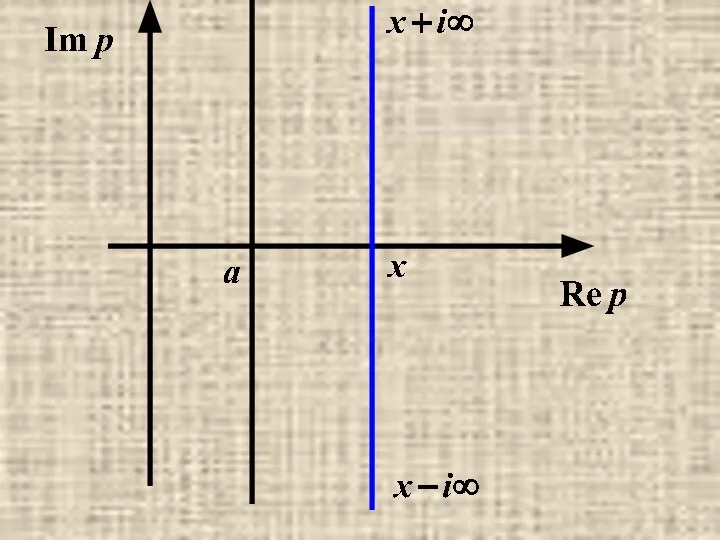
- 25. Замечание. Несобственный интеграл вычисляется вдоль прямой Re p=x>a и понимается в смысле главного значения:
- 27. Доказательство. Рассмотрим и докажем:
- 28. Замечание: на ∀ [0,T] интеграл сходится равномерно по t. 2) Покажем, что I(x , t) не
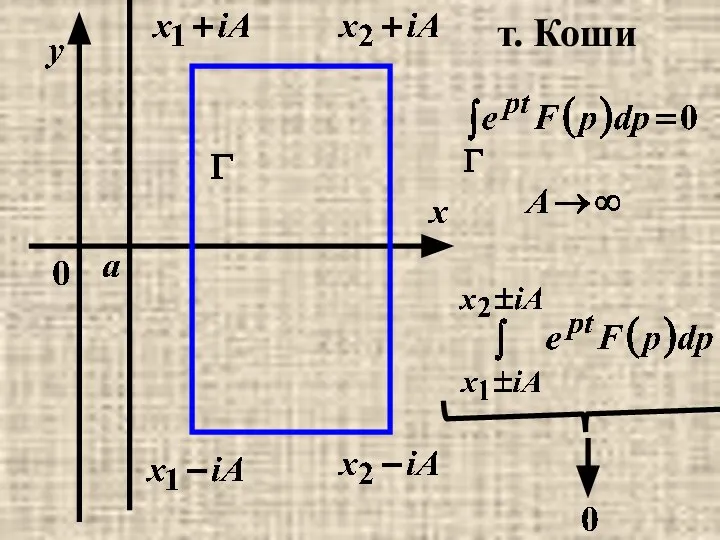
- 29. т. Коши
- 30. интегралы по горизонтальным отрезкам дадут в пределе 0. Интегралы по вертикальным прямым перейдут в несобственные интегралы
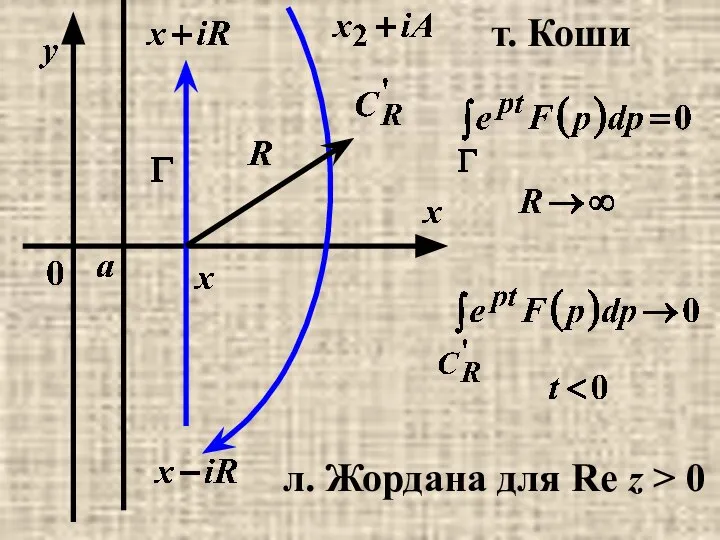
- 31. 3) Докажем, что I ( x , t ) ≡ 0, t Рассмотрим I( x ,
- 32. т. Коши л. Жордана для Re z > 0
- 34. Покажем, что
- 35. =(интеграл можно вычислить с помощью вычетов, учитывая, что контур обходится по часовой стрелке “-”)=
- 36. Замечание. Если ∃ аналитическое продолжение F(p) в левую полуплоскость (Re p
- 37. В частности, если F(p)=1/Pn(p), где все нули полинома Pn(p) лежат в левой полуплоскости Re p
- 38. Пример.
- 41. осциллирующая функция с линейно нарастающей амплитудой- резонанс.
- 42. п.5. Изображение произведения.
- 45. Пример.
- 46. ={при помощи вычетов, с учетом того, что контур интегрирования замыкается вправо и обходится по часовой стрелке-
- 48. Скачать презентацию

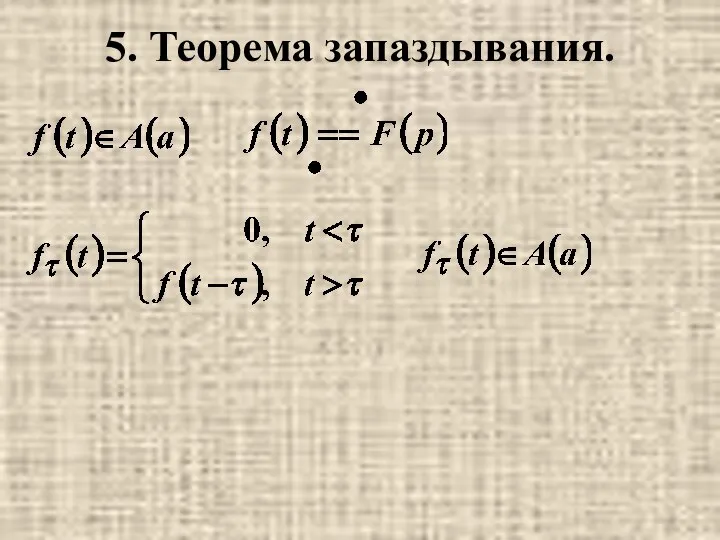
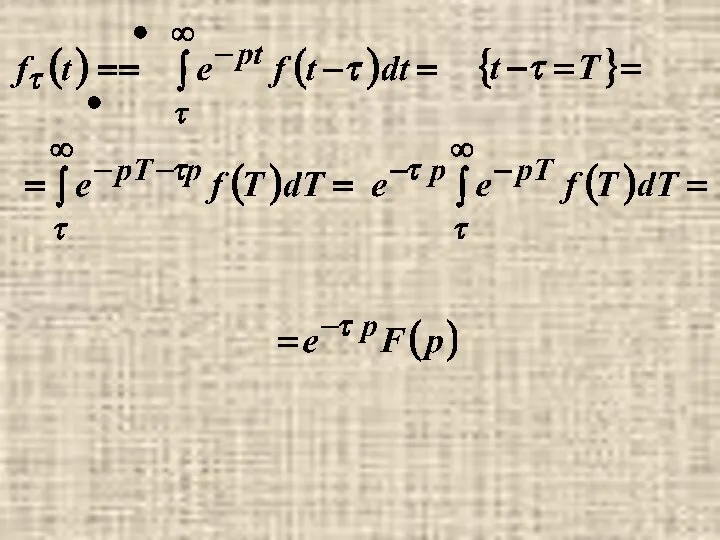
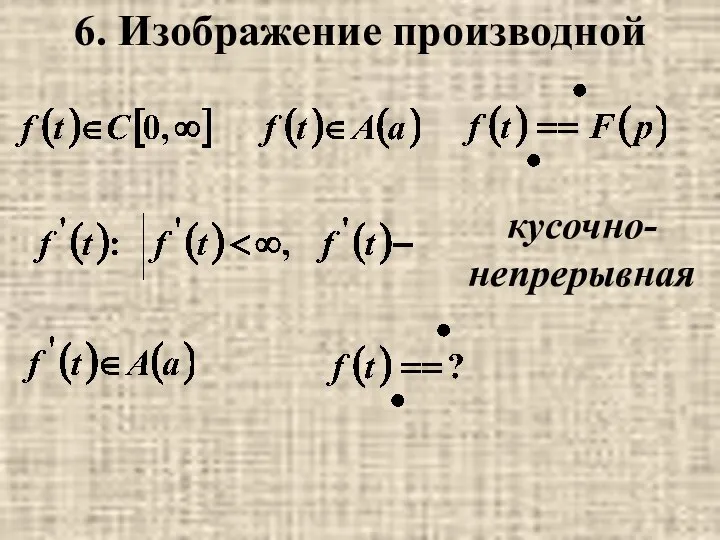
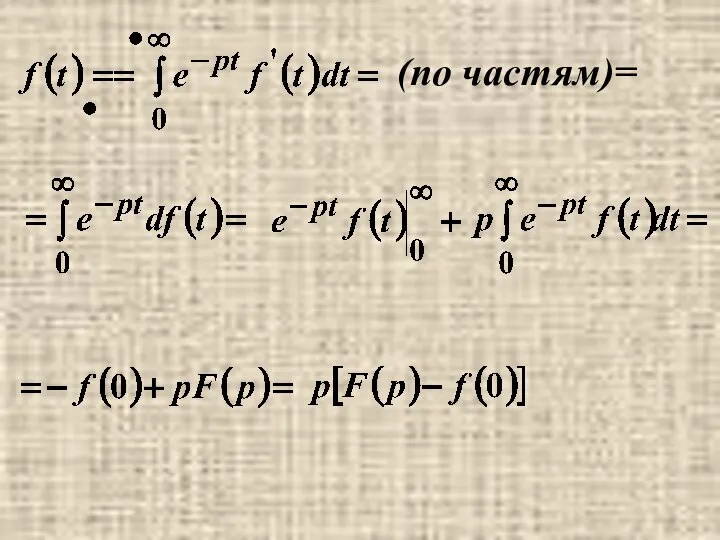
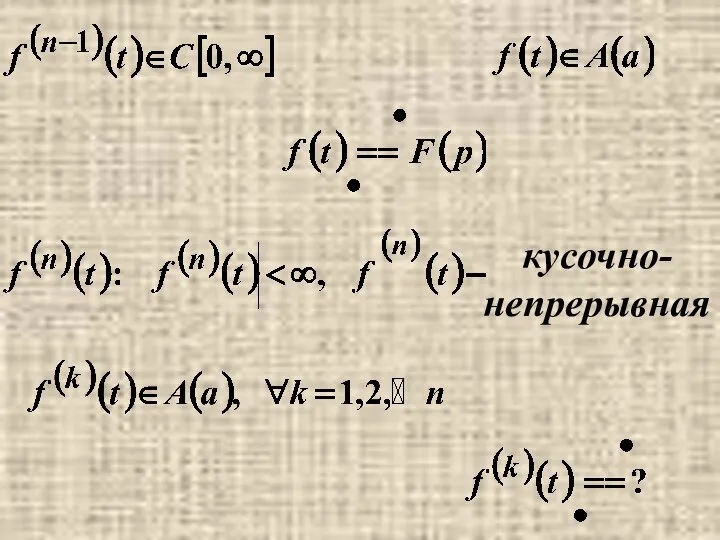
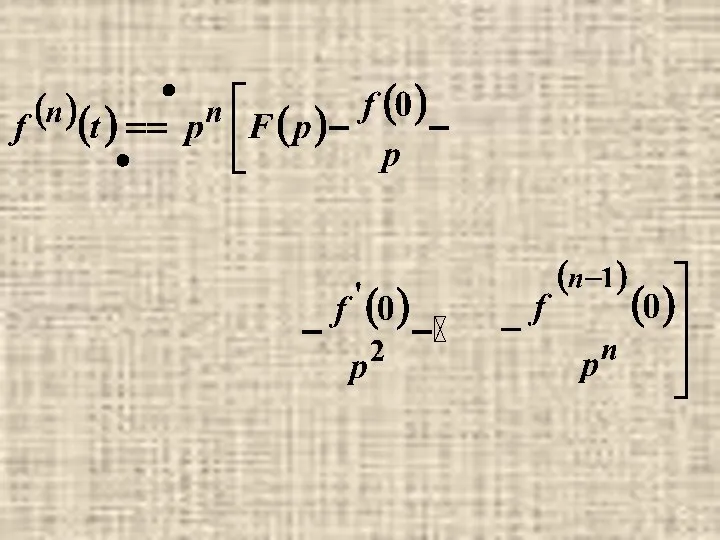
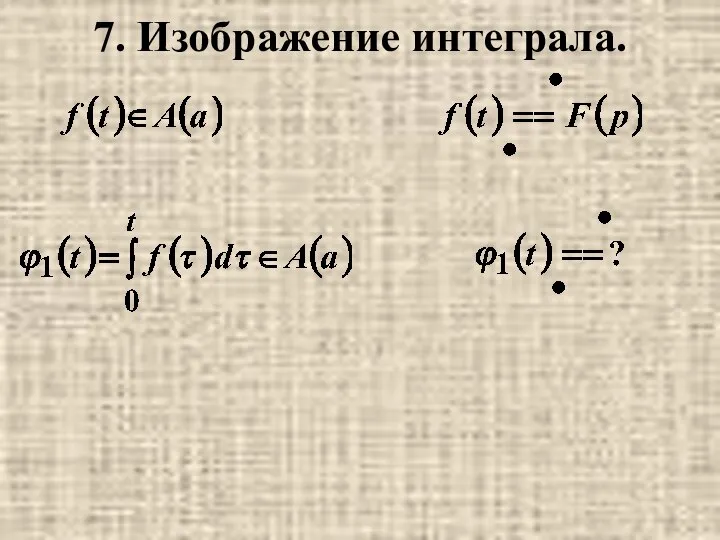
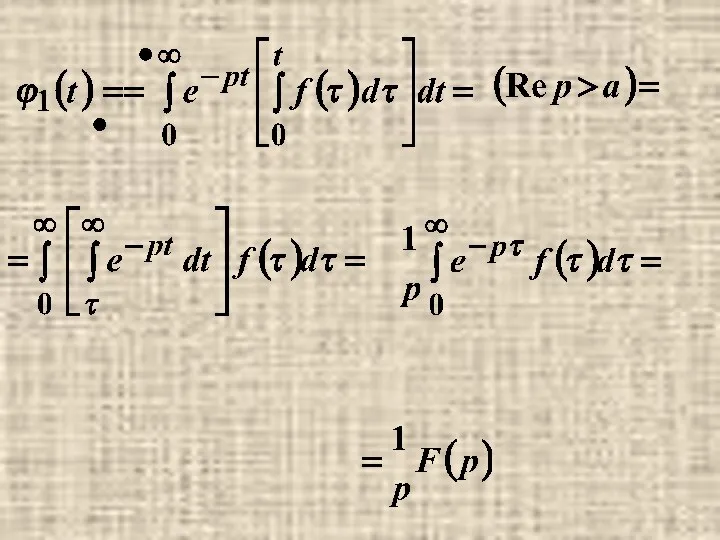
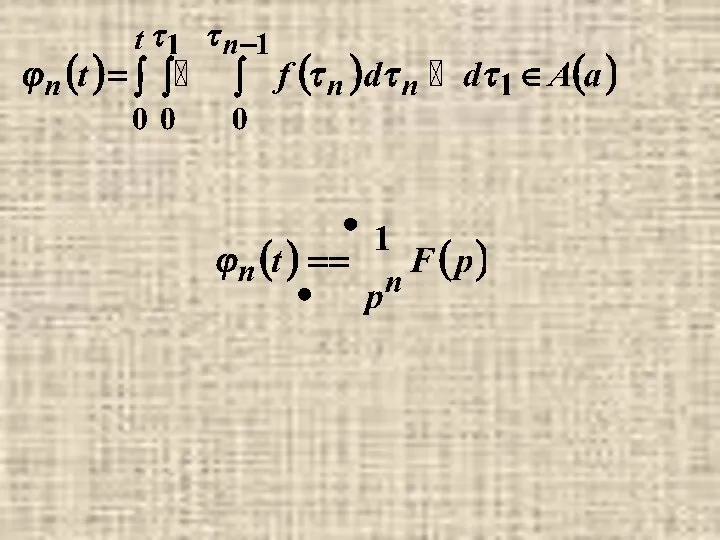
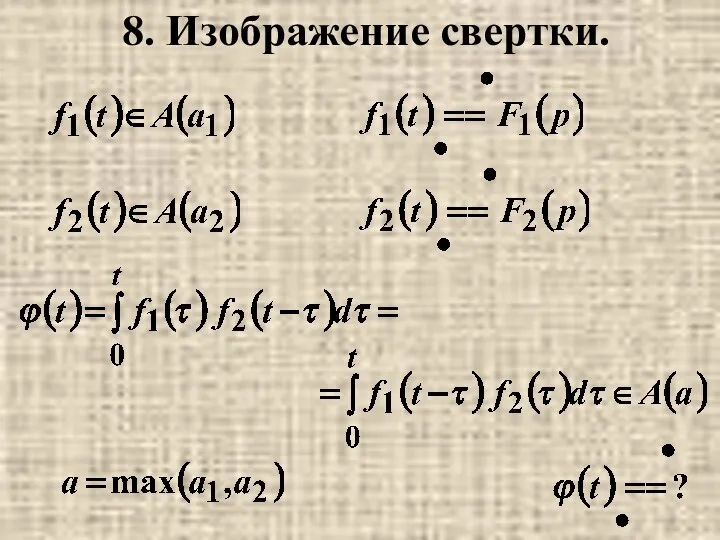


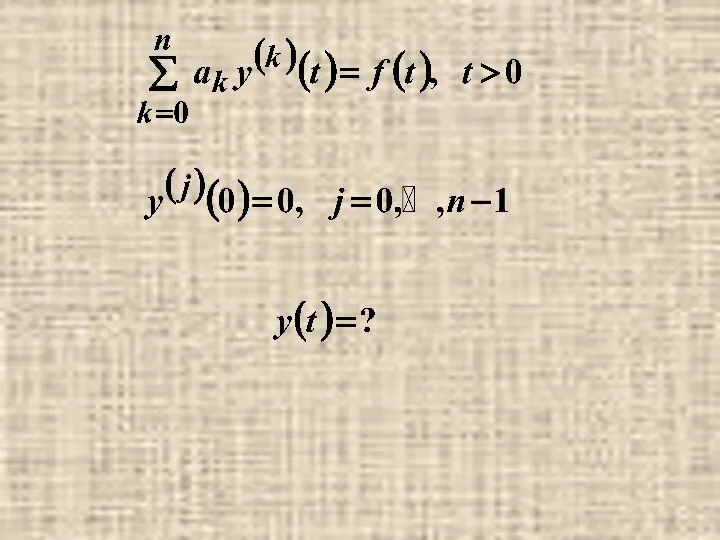
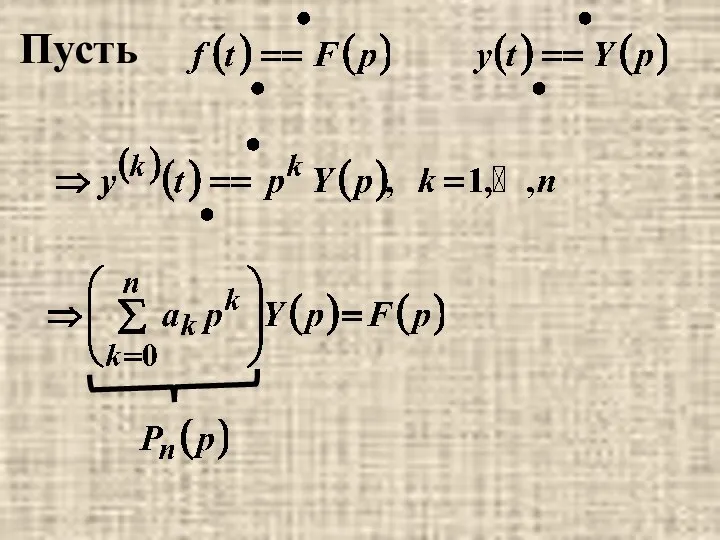
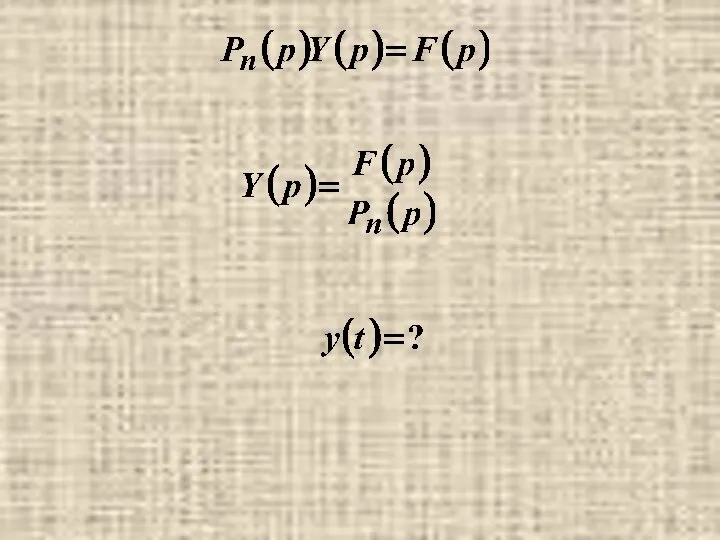
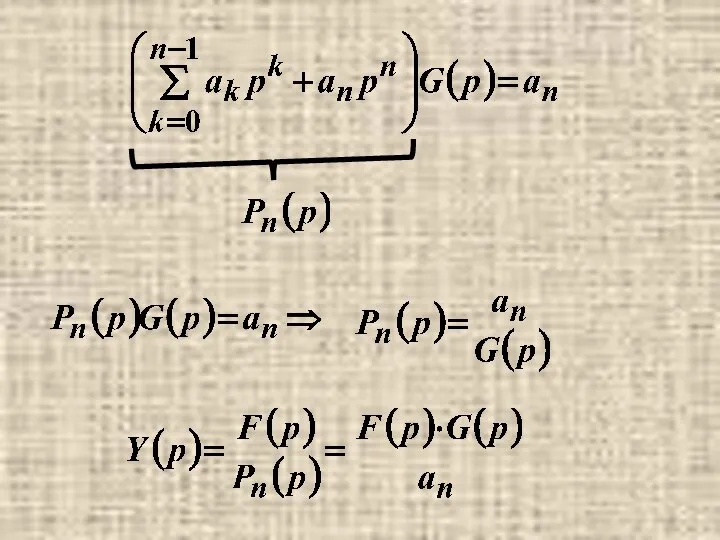
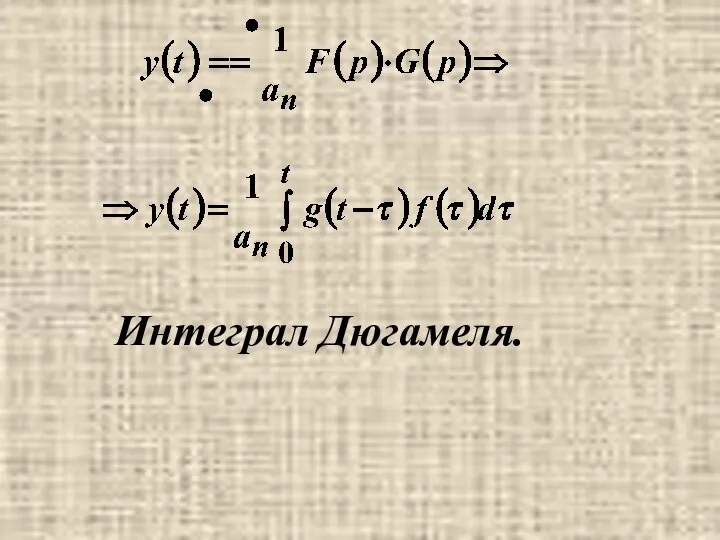

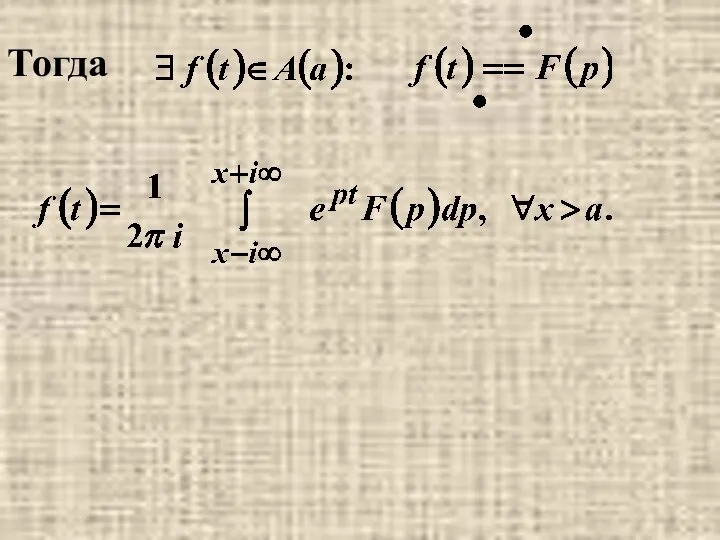

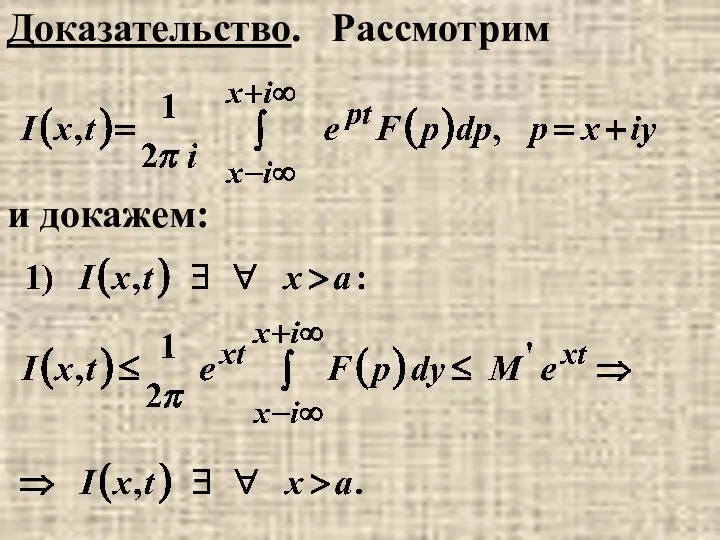
![Замечание: на ∀ [0,T] интеграл сходится равномерно по t. 2) Покажем,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/685719/slide-27.jpg)
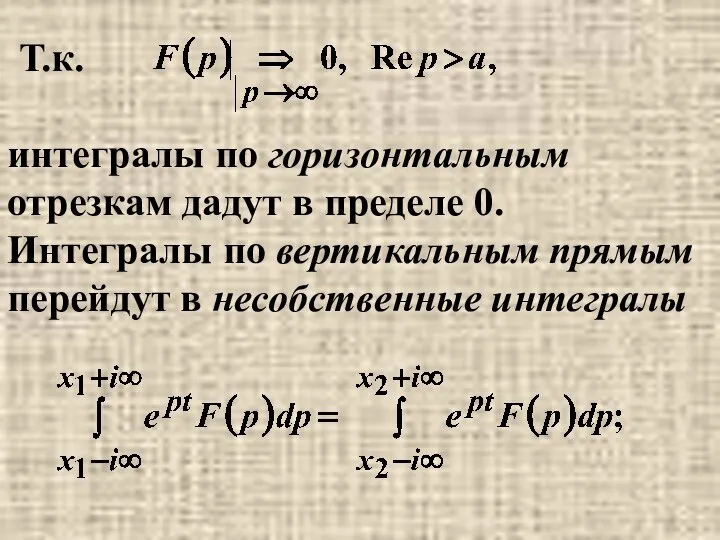


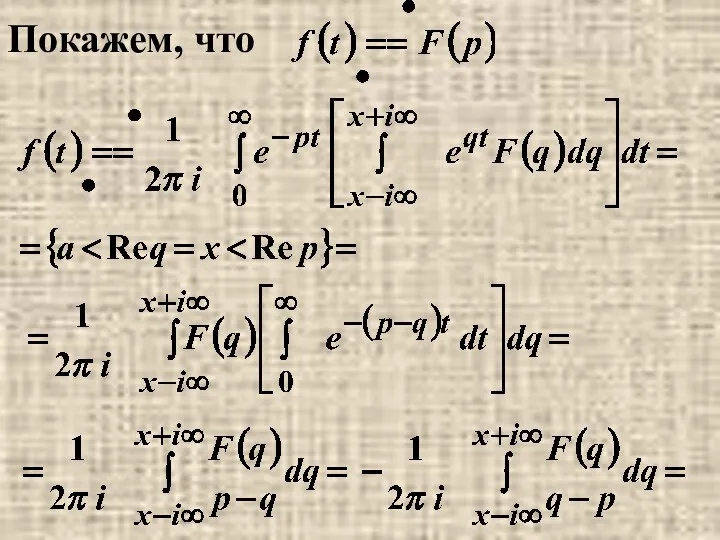

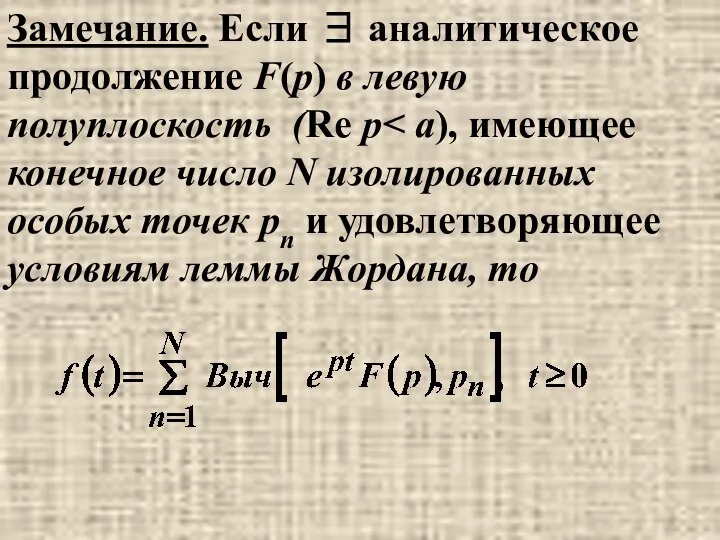

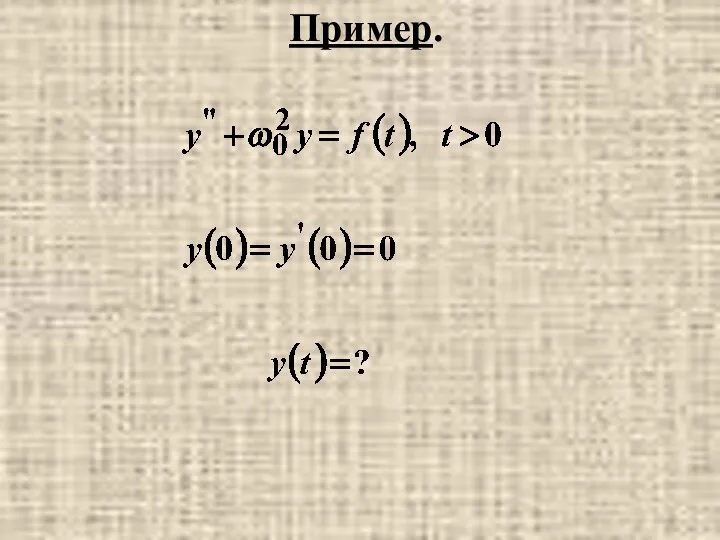
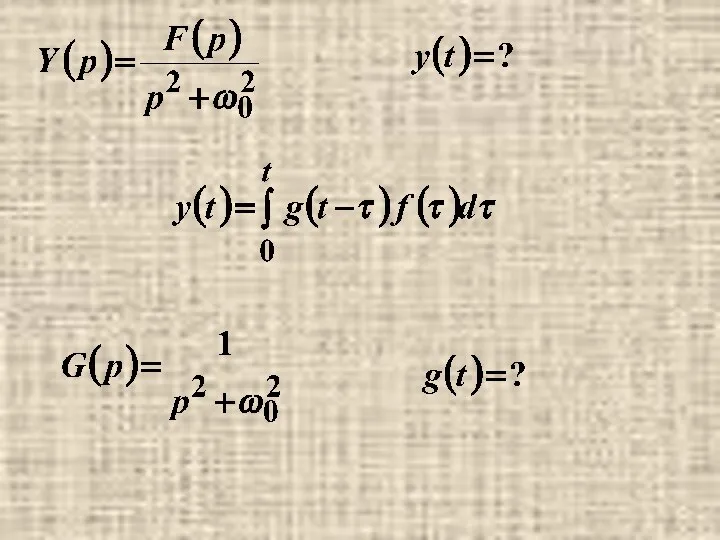
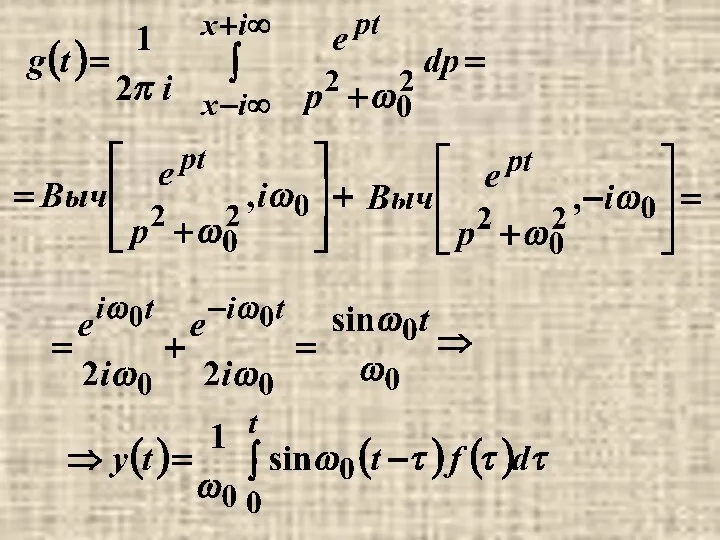
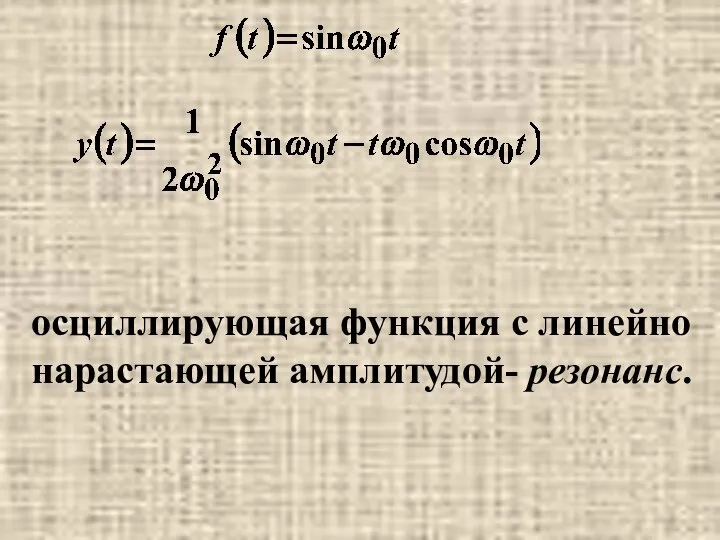
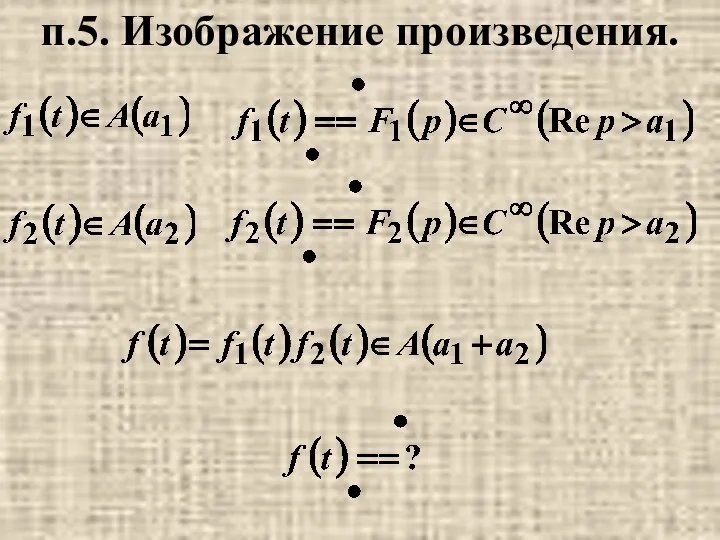
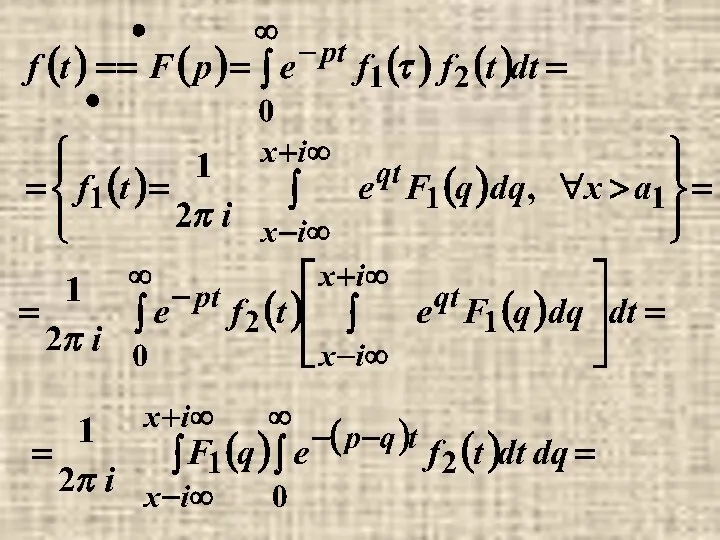
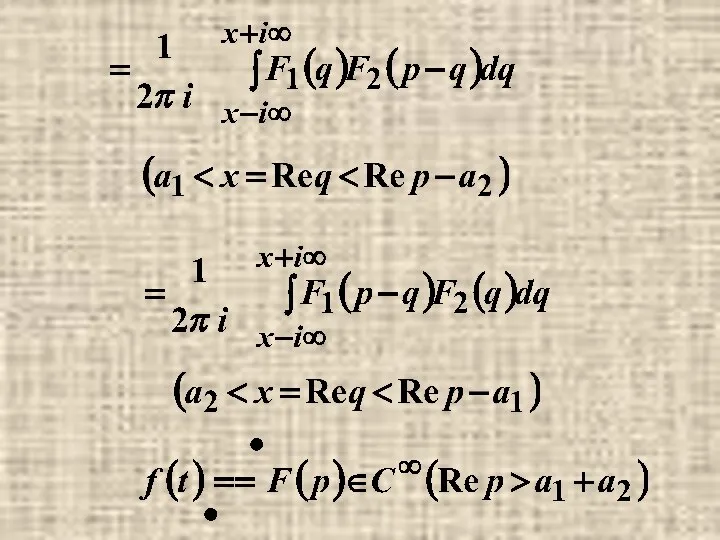
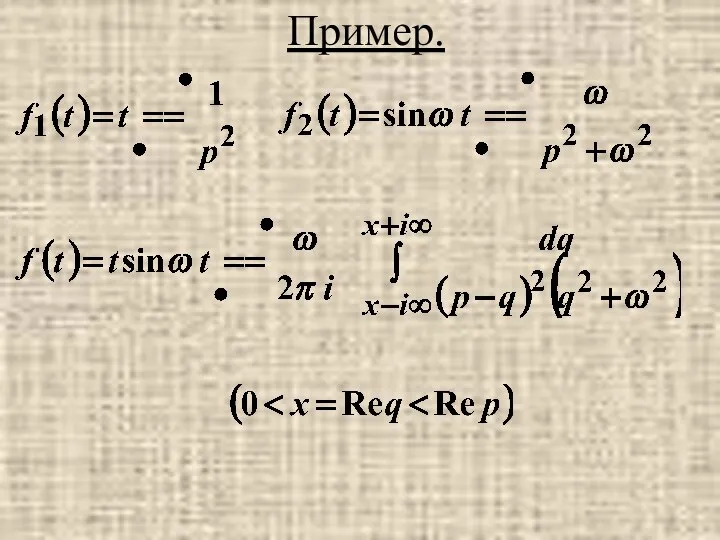

 Подобные слагаемые
Подобные слагаемые Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике Математика для малышей
Математика для малышей Корреляция случайных величин
Корреляция случайных величин Презентация по математике "Нестандартные задачи" - скачать
Презентация по математике "Нестандартные задачи" - скачать  Морской бой. Математическая игра
Морской бой. Математическая игра Условная оптимизация. Лекция 11
Условная оптимизация. Лекция 11 Повторение. Алгебра 9 класс
Повторение. Алгебра 9 класс Признак параллельности прямых. Геометрия 7 класс
Признак параллельности прямых. Геометрия 7 класс Степень с натуральным показателем
Степень с натуральным показателем Уменьшаемое. Вычитаемое. Разность
Уменьшаемое. Вычитаемое. Разность «Дом для гнома» («Состав числа 10» математика 1 класс)
«Дом для гнома» («Состав числа 10» математика 1 класс) Измерения
Измерения Система счисления (задания)
Система счисления (задания) Составление задач на сложение и вычитание по одному рисунку
Составление задач на сложение и вычитание по одному рисунку Решение задания №3 ГИА
Решение задания №3 ГИА Преобразования координат на плоскости
Преобразования координат на плоскости Дәрес барышы
Дәрес барышы Возникновение геометрии
Возникновение геометрии Проект «Золотое сечение»
Проект «Золотое сечение» Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Розв’язання задач на розвиток технічного мислення
Розв’язання задач на розвиток технічного мислення Геометрия части В
Геометрия части В Теорема Пифагора (теорема нимфы, теорема невесты)
Теорема Пифагора (теорема нимфы, теорема невесты) Функции и их графики
Функции и их графики Логические задачи для дошкольников
Логические задачи для дошкольников Решение логарифмических уравнений и неравенств
Решение логарифмических уравнений и неравенств Презентация по математике "Математическое кафе" - скачать бесплатно
Презентация по математике "Математическое кафе" - скачать бесплатно