Содержание
- 2. Для дискретных СВ он выражается формулой: А для непрерывных СВ:
- 3. Выясним смысл этой характеристики. Для этого вычислим корреляционный момент для двух независимых величин Х и У:
- 4. Корреляционный момент двух независимых величин равен нулю. Математическое ожидание произведения независимых случайных величин Х и У
- 5. Следовательно, если корреляционный момент двух случайных величин отличен от нуля, то это есть признак наличия между
- 6. коэффициент корреляции
- 7. Для независимых СВ он также равен нулю. Такие СВ называются некоррелированными. Некорреляция СВ слабее независимости, т.е.
- 8. Вычислим коэффициент корреляции для СВ Х и У из предыдущего примера.
- 9. Коэффициент корреляции характеризует не всякую, а только линейную зависимость, при которой возрастание (убывание) одной СВ приводит
- 10. Вычислим корреляционный момент случайных величин Х и У: По свойству математического ожидания:
- 11. Выражение, стоящее в скобках, по определению является дисперсией Х: С другой стороны, по свойству дисперсии: Тогда
- 12. Таким образом, знак коэффициента корреляции определяется знаком постоянной А. Далее, чтобы показать, что абсолютное значение коэффициента
- 13. Найдем дисперсию Z: (т.к. дисперсия всегда неотрицательна). Тогда
- 15. Скачать презентацию












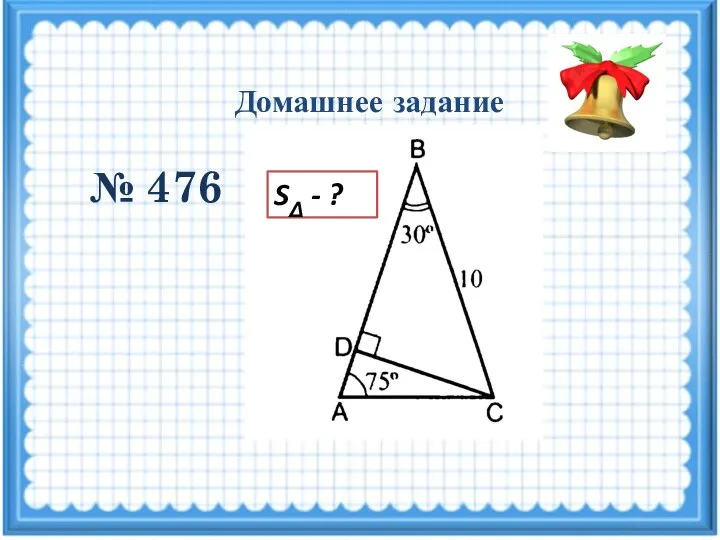 Домашнее задание № 476
Домашнее задание № 476 Перетворення та переміщення подібності. (9 клас)
Перетворення та переміщення подібності. (9 клас) Экспертный метод ранжирования
Экспертный метод ранжирования Реле времени Подготовил: Осипович Сергей 24 А 2 Б
Реле времени Подготовил: Осипович Сергей 24 А 2 Б  Решение заданий ЕГЭ. Урок-консультация. 11 класс
Решение заданий ЕГЭ. Урок-консультация. 11 класс Арккосинус и решение уравнения cos x = a Уроки № 1-2
Арккосинус и решение уравнения cos x = a Уроки № 1-2 Тригонометрия
Тригонометрия Решение одной задачи, не лишено здравого смысла
Решение одной задачи, не лишено здравого смысла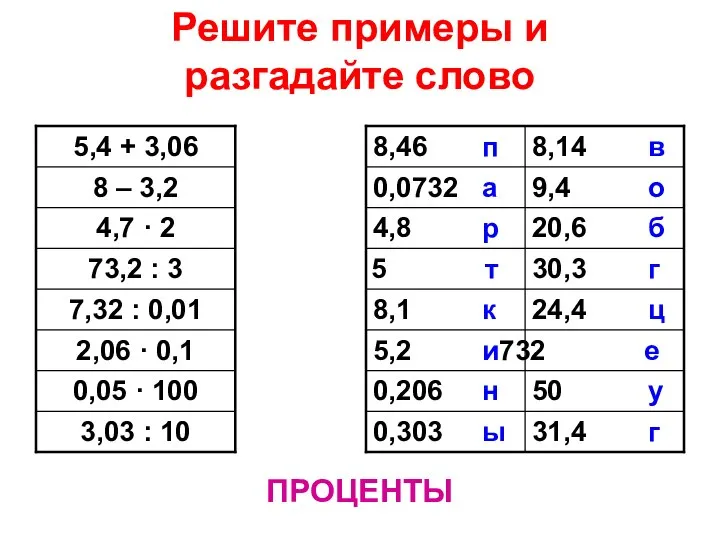 Запись процентов в виде десятичной дроби
Запись процентов в виде десятичной дроби Доказательство теоремы Фалеса (8 класс)
Доказательство теоремы Фалеса (8 класс) Системи лінійних рівнянь
Системи лінійних рівнянь Касательная к окружности. Свойство отрезков касательных
Касательная к окружности. Свойство отрезков касательных Графическое решений квадратных уравнений
Графическое решений квадратных уравнений Математика вокруг нас. Узоры и орнаменты на посуде
Математика вокруг нас. Узоры и орнаменты на посуде Тест по теме: "Взаимное расположение прямых в пространстве. Параллельность прямых, прямой и плоскости"
Тест по теме: "Взаимное расположение прямых в пространстве. Параллельность прямых, прямой и плоскости" Самостоятельная работа. Постройте график функции
Самостоятельная работа. Постройте график функции Объект социально-экономической статистики
Объект социально-экономической статистики Длина окружности
Длина окружности Динамические модели LOGO
Динамические модели LOGO Метод математической индукции
Метод математической индукции Задачи к уроку «Прямоугольный параллелепипед. Куб» 5 класс
Задачи к уроку «Прямоугольный параллелепипед. Куб» 5 класс Презентация на тему Векторы в пространстве
Презентация на тему Векторы в пространстве  Презентация на тему Арифметические действия над числами.
Презентация на тему Арифметические действия над числами. Умение читать свойства функции по графику
Умение читать свойства функции по графику Задачи на нахождение наибольшего и наименьшего значений величин. 10 класс ( первый урок)
Задачи на нахождение наибольшего и наименьшего значений величин. 10 класс ( первый урок) Интегралы, локальные вклады. (Лекция 3)
Интегралы, локальные вклады. (Лекция 3) КРИСТАЛЛЫ - ПРИРОДНЫЕ МНОГОГРАННИКИ Выполнил ученик 10Б класса Мозговой Иван Учитель: Холявка Н.В.
КРИСТАЛЛЫ - ПРИРОДНЫЕ МНОГОГРАННИКИ Выполнил ученик 10Б класса Мозговой Иван Учитель: Холявка Н.В. Элементы символической логики
Элементы символической логики