Содержание
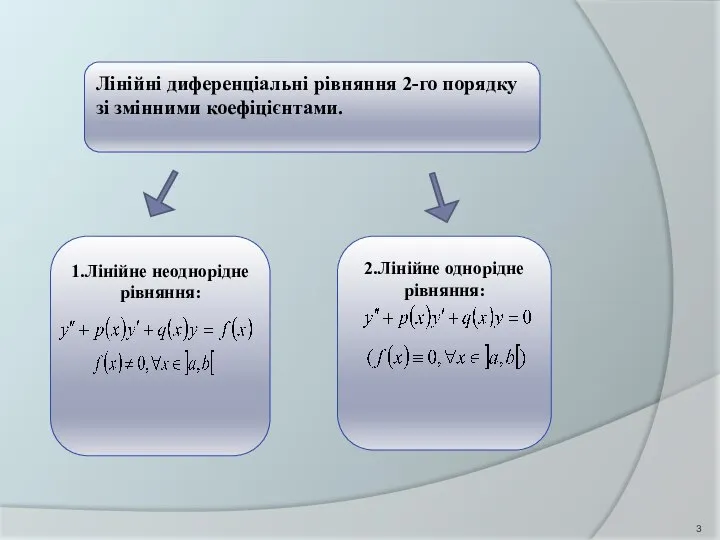
- 2. Тема 14. Лінійні диференціальні рівняння другого порядку. 14.1. Лінійні диференціальні рівняння другого порядку зі змінними коефіцієнтами.
- 3. Лінійні диференціальні рівняння 2-го порядку зі змінними коефіцієнтами. 2.Лінійне однорідне рівняння: 1.Лінійне неоднорідне рівняння:
- 4. Лінійні однорідні рівняння. Властивості розв’язків. Теорема. Якщо − частинні розв’язки однорідного рівняння , (14.1) то функція
- 5. Визначник Вронського. Для двох функцій , розв’язків рівняння (14.1)) визначником Вронського (або вронскіаном) називається визначник другого
- 6. Лінійно залежні функції. 1. Функції , називаються лінійно залежними на інтервалі , якщо існують такі 2
- 7. Лінійно незалежні функції. 1.Функції , називаються лінійно незалежними на інтервалі , якщо тотожність (14.4) де ,
- 8. Загальний розв’язок однорідного рівняння. Теорема. Якщо функції та лінійно незалежні на розв’язки однорідного рівняння (14.1) то
- 9. Знаходження загального розв’язку однорідного рівняння. Теорема. Якщо відомий один частинний розв’язок лінійного однорідного рівняння (14.1), то
- 10. Приклад 14.1. Знайти загальний розв’язок рівняння Зведемо рівняння до вигляду (14.1), розділивши на вираз : Один
- 11. Структура загального розв’язку неоднорідного рівняння. Теорема. Загальний розв’язок лінійного неоднорідного рівняння (14.7) складається з суми загального
- 12. Окремі випадки знаходження частинного розв’язку неоднорідного рівняння. Розглянемо неоднорідне диференціальне рівняння вигляду (14.8) Нехай − частинний
- 13. Метод варіації довільних сталих (метод Лагранжа). 2. Загальний розв’язок лінійного неоднорідного рівняння (14.7) шукаємо у вигляді
- 14. Приклад 14.3. Розв’язати рівняння Маємо рівняння вигляду (14.1). Складемо відповідне йому однорідне рівняння , його загальний
- 15. Продовження прикладу 14.3. , , і, згідно з формулами Крамера, , Інтегруючи ці диференціальні рівняння, ,
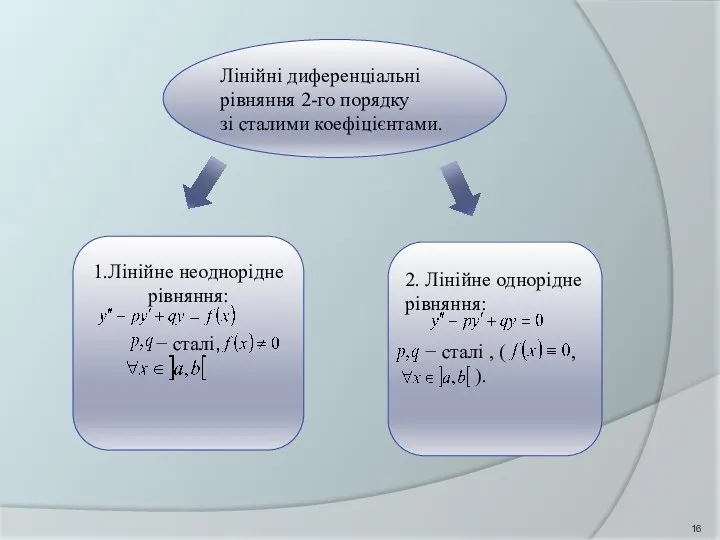
- 16. Лінійні диференціальні рівняння 2-го порядку зі сталими коефіцієнтами. 1.Лінійне неоднорідне рівняння: − сталі, 2. Лінійне однорідне
- 17. Метод Ейлера Застосовуємо заміну Ейлера , до однорідного рівняння Приходимо до характеристичного рівняння Тут можливі три
- 18. Приклад 14.4. Розв’язати задачу Коші: , , . Характеристичне рівняння має корені , , отже загальний
- 19. Метод невизначених коефіцієнтів. Якщо права частина неоднорідного рівняння (14.14) спеціального вигляду , (14.15) де - сталі,
- 20. Приклад 14.5. Розв’язати рівняння . Характеристичне рівняння має корені , , , тому загальний розв’язок однорідного
- 22. Скачать презентацию

















 Аттестационная работа. Методическая разработка Проектноисследовательская деятельность учащихся на уроках математики
Аттестационная работа. Методическая разработка Проектноисследовательская деятельность учащихся на уроках математики Подготовка к МСО
Подготовка к МСО Упражнения к главе 1
Упражнения к главе 1 Решение систем уравнений с двумя неизвестными
Решение систем уравнений с двумя неизвестными Великие математики
Великие математики Измерение углов
Измерение углов Ох,уж эта математика! Команды «Квадрат и Звезды»
Ох,уж эта математика! Команды «Квадрат и Звезды» Устный счет
Устный счет Функции и их свойства
Функции и их свойства Площадь. Формула площади прямоугольника
Площадь. Формула площади прямоугольника Математика 3 класс, II четверть Тема урока Решение задач.
Математика 3 класс, II четверть Тема урока Решение задач.  Возведение степени в степень
Возведение степени в степень Обратные тригонометрические функции
Обратные тригонометрические функции Основные понятия и аксиомы стереометрии
Основные понятия и аксиомы стереометрии Исследование функций. Задачи типа В12 в ЕГЭ
Исследование функций. Задачи типа В12 в ЕГЭ Повторение. (5 класс. Урок 3)
Повторение. (5 класс. Урок 3) Умножение дробей
Умножение дробей Свойства параллелограмма
Свойства параллелограмма Алгебра и начала анализа. 9-10 класс. Радианная мера углов и дуг
Алгебра и начала анализа. 9-10 класс. Радианная мера углов и дуг Матричная алгебра в экономике
Матричная алгебра в экономике Показательные уравнения
Показательные уравнения Степень с натуральным показателем
Степень с натуральным показателем Брейн - ринг. Математическая игра
Брейн - ринг. Математическая игра Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии
Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии Решение задач. Теорема Пифагора
Решение задач. Теорема Пифагора Преподавание элементов теории вероятности и статистики в 5-9 классах. Система подготовки учащихся к итоговой аттестации
Преподавание элементов теории вероятности и статистики в 5-9 классах. Система подготовки учащихся к итоговой аттестации Линейная алгебра
Линейная алгебра Где встречаются многогранники и в каких областях могут применяться
Где встречаются многогранники и в каких областях могут применяться