Содержание
- 2. Историческая справка Впервые логарифмическая спираль упоминается в письме Декарта к Мерсену в 1638г., в котором Декарт
- 3. Определение Логарифмической спиралью называется кривая, выражаемая в полярной системе уравнением: где p – расстояние от произвольной
- 4. Построение Построение логарифмической спирали может быть осуществлено по точкам и с помощью специального прибора. Построение по
- 5. Построение с помощью специального прибора Прибор для вычерчивания логарифмической спирали состоит из стержня АВ, к одному
- 6. Уравнения Уравнение в полярных координатах (полюс совпадает с полюсом спирали; полярная ось проведена через произвольно взятую
- 7. Свойства Угол μ, составляемый касательной в произвольной точке логарифмической спирали с радиусом-вектором точки касания за висит
- 8. Радиус кривизны в произвольной точке логарифмической спирали пропорционален радиусу-вектору этой точки. Длина дуги логарифмической спирали равняется
- 9. Длина дуги логарифмической спирaли от полюса до произвольной точки ее равна длине полярной касательной; про· веденной
- 10. Логарифмическая спираль в технике и природе Нож соломорезки
- 12. Скачать презентацию









 Теорема Піфагора
Теорема Піфагора Отношения и отображения
Отношения и отображения Наибольший общий делитель. Взаимно простые числа
Наибольший общий делитель. Взаимно простые числа Проект – исследование по теме «Теория случайностей» Выполнила: ученица 9 класса Бтикова Алина Руководитель: учитель матема
Проект – исследование по теме «Теория случайностей» Выполнила: ученица 9 класса Бтикова Алина Руководитель: учитель матема Задачи на готовых чертежах. Четырехугольники
Задачи на готовых чертежах. Четырехугольники Показательные уравнения и неравенства
Показательные уравнения и неравенства Виды треугольников
Виды треугольников Яковлева Ксения ученица 11 класса МБОУ «СОШ№22» г. Анжеро-Судженск, Кемеровской области Научный руководитель: Лилия Геннадьевна
Яковлева Ксения ученица 11 класса МБОУ «СОШ№22» г. Анжеро-Судженск, Кемеровской области Научный руководитель: Лилия Геннадьевна Обыкновенные дроби. (Урок 48)
Обыкновенные дроби. (Урок 48) Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Свойства функций. Непрерывность в точке
Свойства функций. Непрерывность в точке Вычислительная математика: термины и определения
Вычислительная математика: термины и определения Учебники математики
Учебники математики Современное метрологическое обеспечение. Средства измерения в системах ГХ
Современное метрологическое обеспечение. Средства измерения в системах ГХ Неклассические логики. (Глава 6)
Неклассические логики. (Глава 6) Изучение нумерации чисел в концентре 1000 и в концентре многозначные числа в начальной школе по программе 2100
Изучение нумерации чисел в концентре 1000 и в концентре многозначные числа в начальной школе по программе 2100 Число π
Число π Применение производной и интегралов в различных областях биологии и химии
Применение производной и интегралов в различных областях биологии и химии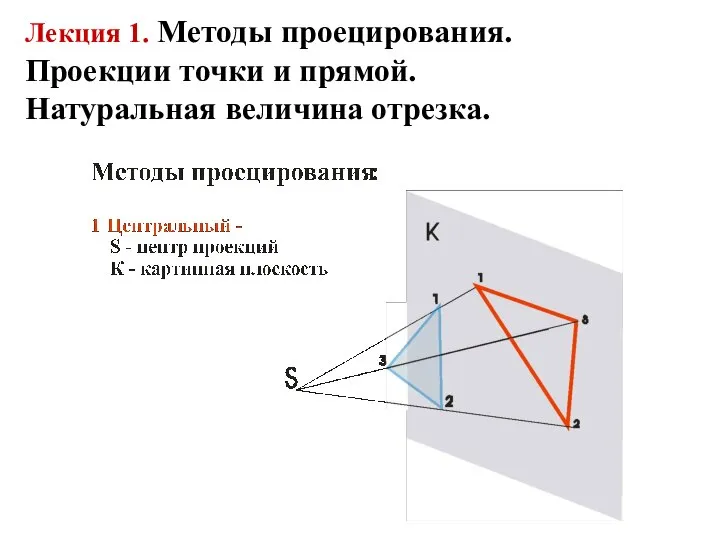 Лекция 1. Методы проецирования. Проекции точки и прямой. Натуральная величина отрезка
Лекция 1. Методы проецирования. Проекции точки и прямой. Натуральная величина отрезка Комбинаторная задача с монетами
Комбинаторная задача с монетами Золотое сечение
Золотое сечение Функции1
Функции1 Уравнение прямой на плоскости
Уравнение прямой на плоскости  Сравнение дробей с одинаковыми знаменателями
Сравнение дробей с одинаковыми знаменателями Угол. Геометрические фигуры
Угол. Геометрические фигуры Числовые выражения
Числовые выражения Объем тел
Объем тел Деление двузначного числа на однозначное
Деление двузначного числа на однозначное