Содержание
- 2. Отношения Определение. Пусть X и Y - два произвольных множества. Если какому-либо элементу x∈X по некоторому
- 3. Не исключено, что X=Y, тогда говорят, что отношение установлено между элементами множества X. Отношения могут обозначаться
- 4. xRy, x∈X, y∈Y - x и y находятся в отношении R. xRy, x∈X, y∈Y - x
- 5. Рассмотрим отношение R между множествами X и Y. Графиком отношения R называется множество Γ={(x,y)|x∈X, y∈Y, xRy}⊇X×Y.
- 8. Всякое отношение имеет график - некоторое подмножество декартового произведения X и Y, и наоборот, всякое подмножество
- 9. Отношение эквивалентности Определение. Отношение R, заданное на множестве X, называется отношением эквивалентности, если оно обладает следующими
- 11. С отношением эквивалентности тесно связано разбиение множества на классы. Определение. Множество X разбито на классы (подмножества),
- 13. Отношение > Определение. Отношение > заданное на множестве X называется отношением частичного строгого порядка, если оно
- 14. Отношение ≥ Определение. Отношение ≥, заданное на множестве X, назывется отношением частичного нестрогого порядка, если выполнены
- 15. Множество X, в котором определены отношения частичного порядка (строгие и нестрогие) называется частично упорядоченным.
- 16. Отображения Пусть X и Y - два произвольных множества. Определение. Соответствие, при котором каждому из элементов
- 17. Множество X называется областью определения отображения и обозначается X=D(f). E(f) называется множеством значений отображения, и E(f)={y∈Y|∃x∈X,
- 18. Пусть f - некоторое отображение из множества X в множество Y. Если x при этом отображении
- 20. Определение. Совокупность всех элементов из множества X, образом которых является y из Y, называется полным прообразом
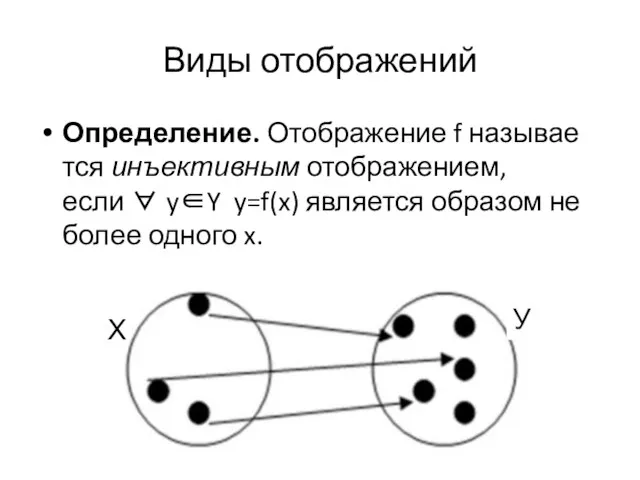
- 22. Виды отображений Определение. Отображение f называется инъективным отображением, если ∀ y∈Y y=f(x) является образом не более
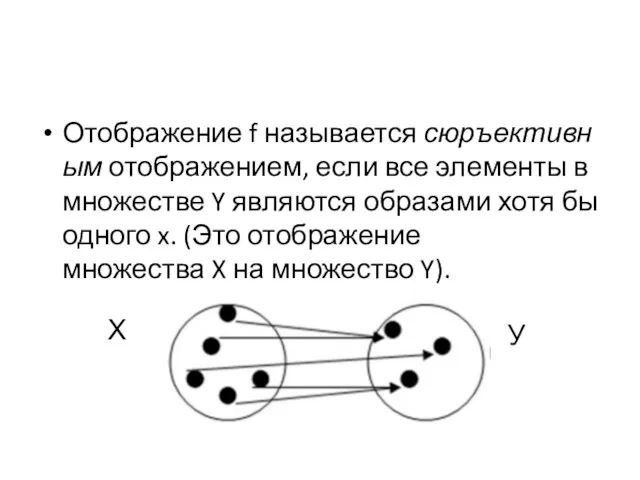
- 23. Отображение f называется сюръективным отображением, если все элементы в множестве Y являются образами хотя бы одного
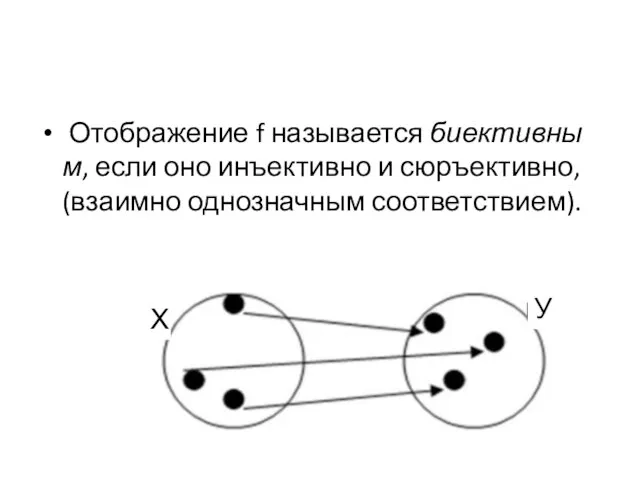
- 24. Отображение f называется биективным, если оно инъективно и сюръективно, (взаимно однозначным соответствием). Х У
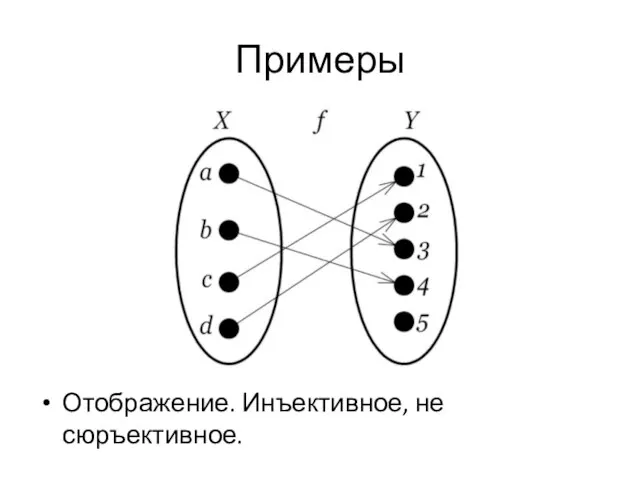
- 25. Примеры Отображение. Инъективное, не сюръективное.
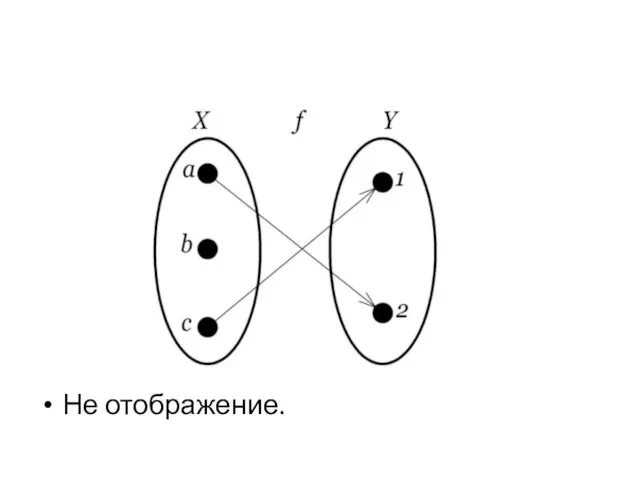
- 26. Не отображение.
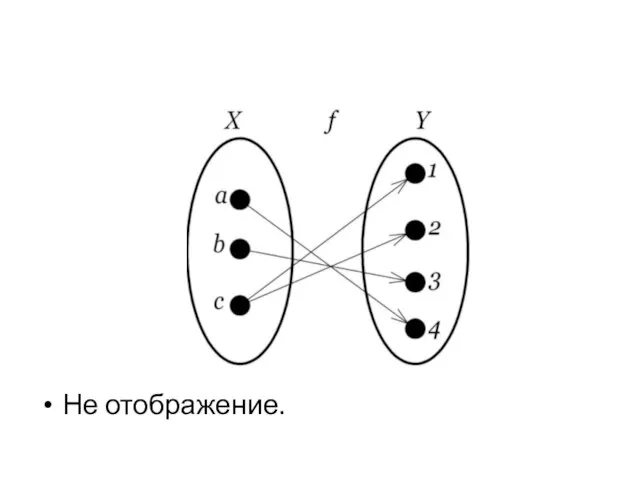
- 27. Не отображение.
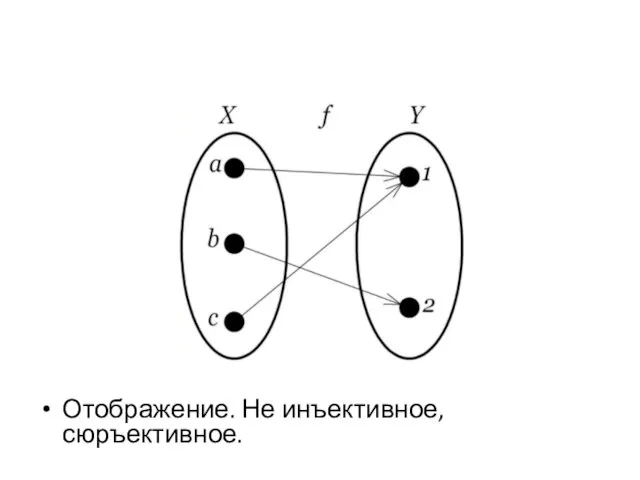
- 28. Отображение. Не инъективное, сюръективное.
- 30. Скачать презентацию




















 Простейшие задачи в координатах
Простейшие задачи в координатах Как помочь учащимся легче воспринимать новый материал
Как помочь учащимся легче воспринимать новый материал Таблица умножения на 6
Таблица умножения на 6 Matlab. Математические вычисления
Matlab. Математические вычисления Основное свойство дроби
Основное свойство дроби Алгоритм решения биквадратного уравнения
Алгоритм решения биквадратного уравнения Артамонова Л.В, учитель математики МКОУ «Москаленский лицей»
Артамонова Л.В, учитель математики МКОУ «Москаленский лицей»  Исполнение линейного алгоритма. Подготовка к ГИА. (Задания В8)
Исполнение линейного алгоритма. Подготовка к ГИА. (Задания В8) Презентация по математике "Функция у=ах^2, её свойства и график" - скачать бесплатно
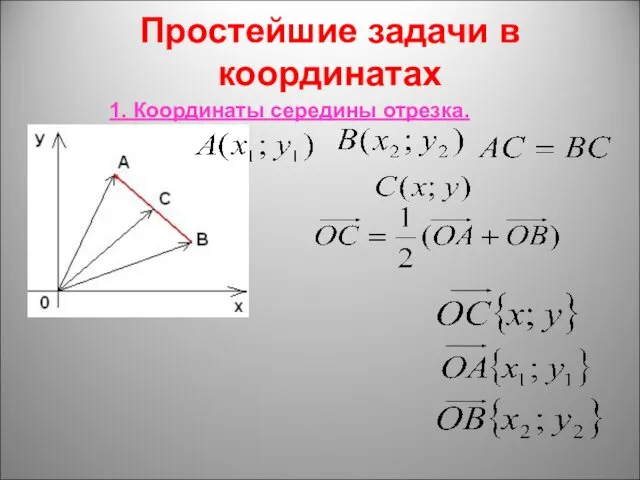
Презентация по математике "Функция у=ах^2, её свойства и график" - скачать бесплатно Координаты середины отрезка.
Координаты середины отрезка.  Сложение и вычитание десятичных дробей. Урок - путешествие
Сложение и вычитание десятичных дробей. Урок - путешествие Сумма углов треугольника
Сумма углов треугольника Неделя предметов естественно-математического цикла
Неделя предметов естественно-математического цикла Решение задач с параметром, сводящихся к исследованию корней квадратного трехчлена
Решение задач с параметром, сводящихся к исследованию корней квадратного трехчлена Процесс решения задачи, как вид деятельности учащихся
Процесс решения задачи, как вид деятельности учащихся Из истории систем счисления
Из истории систем счисления Геометрическое место точек
Геометрическое место точек Работа учителя математики МОУ «СОШ №42» г. Воркуты Курылевой Э. Р.
Работа учителя математики МОУ «СОШ №42» г. Воркуты Курылевой Э. Р.  Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна
Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна  Презентация по математике "Сравнение чисел. Графы" - скачать бесплатно
Презентация по математике "Сравнение чисел. Графы" - скачать бесплатно Простая арифметическая задача
Простая арифметическая задача Язык геометрических рисунков
Язык геометрических рисунков Математические аспекты двухмерной машинной графики
Математические аспекты двухмерной машинной графики Перетворення графіків функцій
Перетворення графіків функцій Масштаб. Виды масштаба
Масштаб. Виды масштаба Сложение и вычитание смешанных чисел. Урок - игра
Сложение и вычитание смешанных чисел. Урок - игра Познакомить с приёмом письменного умножения. Совершенствовать вычислительные навыки и умения решать задачи.
Познакомить с приёмом письменного умножения. Совершенствовать вычислительные навыки и умения решать задачи. Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций