Содержание
- 2. Логическое отрицание (инверсия) Логическое отрицание образуется из высказывания с помощью добавления частицы «не» к сказуемому или
- 3. Таблица истинности для инверсии Из таблицы истинности следует, что инверсия высказывания истинна, когда высказывание ложно.
- 4. Логическое умножение (конъюнкция) Логическое умножение образуется соединением двух высказываний в одно с помощью союза «и». Например:
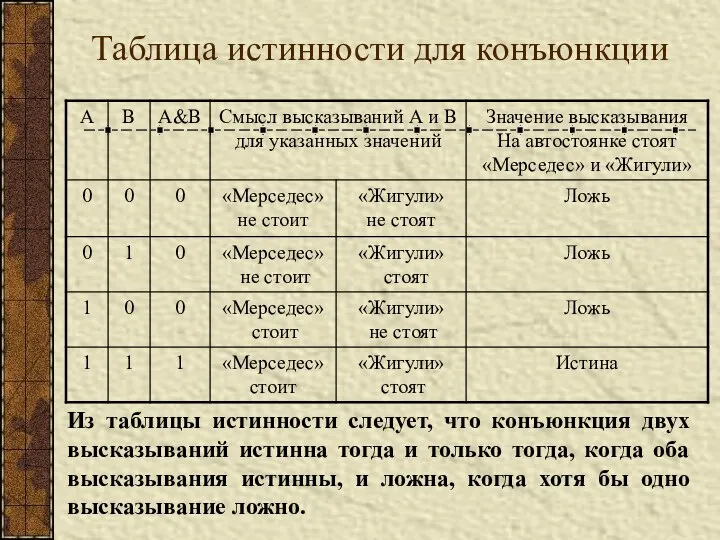
- 5. Таблица истинности для конъюнкции Из таблицы истинности следует, что конъюнкция двух высказываний истинна тогда и только
- 6. Логическое сложение (дизъюнкция) Логическое сложение образуется соединением двух высказываний в одно с помощью союза «или». Например:
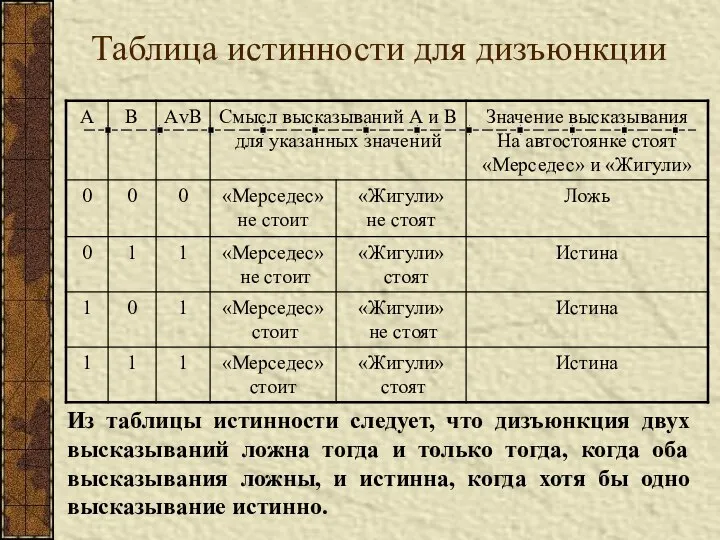
- 7. Таблица истинности для дизъюнкции Из таблицы истинности следует, что дизъюнкция двух высказываний ложна тогда и только
- 8. Логическое следование (импликация) Логическое следование образуется соединением двух высказываний в одно с помощью оборота речи «если
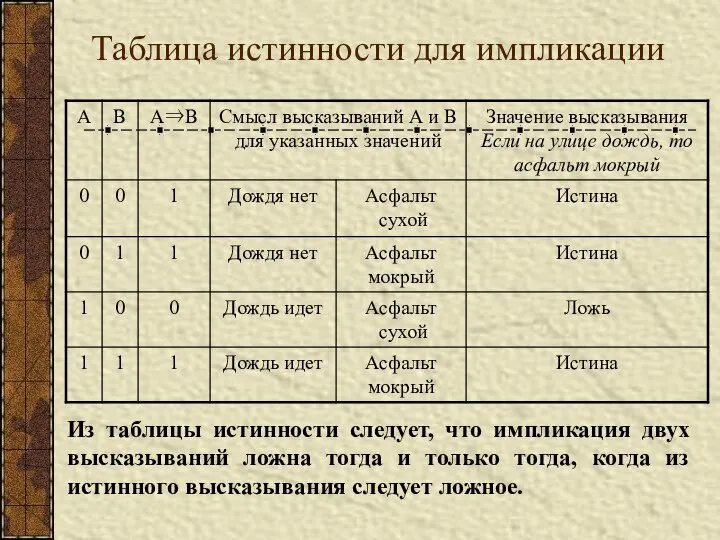
- 9. Таблица истинности для импликации Из таблицы истинности следует, что импликация двух высказываний ложна тогда и только
- 10. Логическое равенство (эквивалентность) Логическое равенство образуется соединением двух высказываний в одно с помощью оборота речи «…тогда
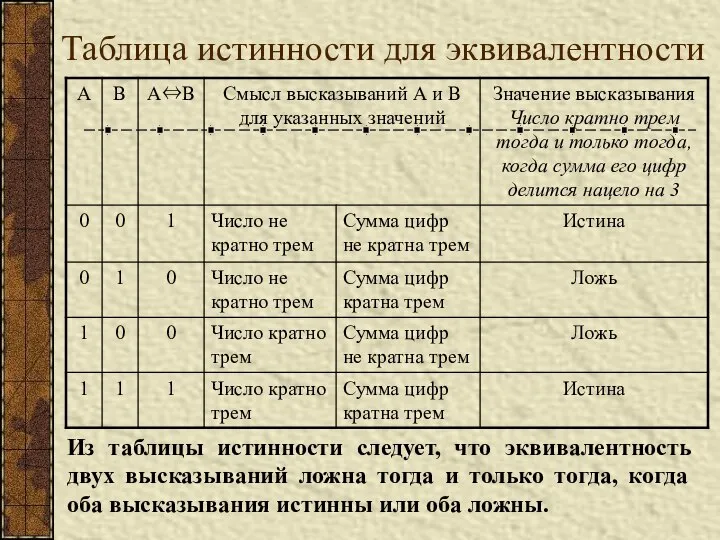
- 11. Таблица истинности для эквивалентности Из таблицы истинности следует, что эквивалентность двух высказываний ложна тогда и только
- 13. Скачать презентацию






 Графика в координатах Автор: Стафеева Елизавета
Графика в координатах Автор: Стафеева Елизавета Вычитание дробей с разными знаменателями
Вычитание дробей с разными знаменателями Элементы теории вероятностей. Элементы комбинаторики. (Лекция 3.4)
Элементы теории вероятностей. Элементы комбинаторики. (Лекция 3.4) Признак подобия треугольников. Урок 32
Признак подобия треугольников. Урок 32 Аттестационная работа. Исследовательская работа "Проценты, проценты, проценты"
Аттестационная работа. Исследовательская работа "Проценты, проценты, проценты" Взаимосвязь математики и архитектуры в симметрии
Взаимосвязь математики и архитектуры в симметрии Таблица умножения и деления на 3
Таблица умножения и деления на 3 Распределительное свойство умножения
Распределительное свойство умножения Среднее арифметическое, размах и мода
Среднее арифметическое, размах и мода Задачи по математике
Задачи по математике Математическая логика. Логические операции и высказывания
Математическая логика. Логические операции и высказывания Функциональные уравнения в школьном курсе математики
Функциональные уравнения в школьном курсе математики Полуплоскость. Луч. Прямая
Полуплоскость. Луч. Прямая Симметрия
Симметрия Презентация по математике "Введение вероятностно-статистической линии в школьный курс математики 5-6 классов" - скачать
Презентация по математике "Введение вероятностно-статистической линии в школьный курс математики 5-6 классов" - скачать  Векторы плоскости
Векторы плоскости Действия с обыкновенными дробями. Умножение и деление
Действия с обыкновенными дробями. Умножение и деление Discrete mathematics
Discrete mathematics Взаимное расположение графиков линейной функции
Взаимное расположение графиков линейной функции Основы теории проверки статистических гипотез
Основы теории проверки статистических гипотез Обозначение натуральных чисел Урок 1 5 класс
Обозначение натуральных чисел Урок 1 5 класс  Деление с остатком
Деление с остатком Касательная к графику функции
Касательная к графику функции Презентация по математике "Натуральное число 5" - скачать бесплатно
Презентация по математике "Натуральное число 5" - скачать бесплатно Производная. Тест по алгебре
Производная. Тест по алгебре История возникновения дробей
История возникновения дробей Решение задач с помощью систем линейных уравнений
Решение задач с помощью систем линейных уравнений Теорема Пифагора
Теорема Пифагора