Содержание
- 2. Маршруты Пусть G =(V, E) – н-граф. Маршрутом в графе G называется чередующаяся последовательность вершин и
- 3. Маршруты Вершина - начальная вершина маршрута М, - конечная, - внутренняя вершина, маршрут соединяющий и .
- 4. Маршруты Маршрут М называется цепью - если его ребра не повторяются, простой цепью – если его
- 5. Маршруты Маршрут М называется циклическим, если начальная и конечная вершина совпадают. Замечание: совпадают, не значит повторяются.
- 6. Маршруты Циклический маршрут М называется циклом - если его ребра не повторяются, простым циклом – если
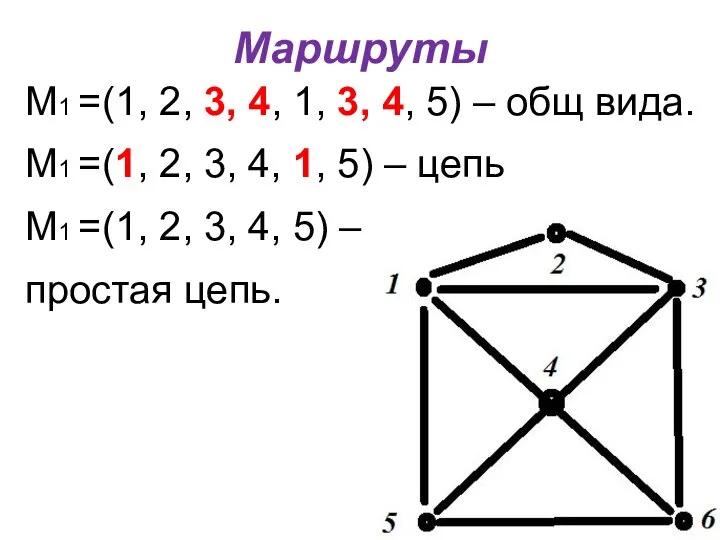
- 7. Маршруты М1 =(1, 2, 3, 4, 1, 3, 4, 5) – общ вида. М1 =(1, 2,
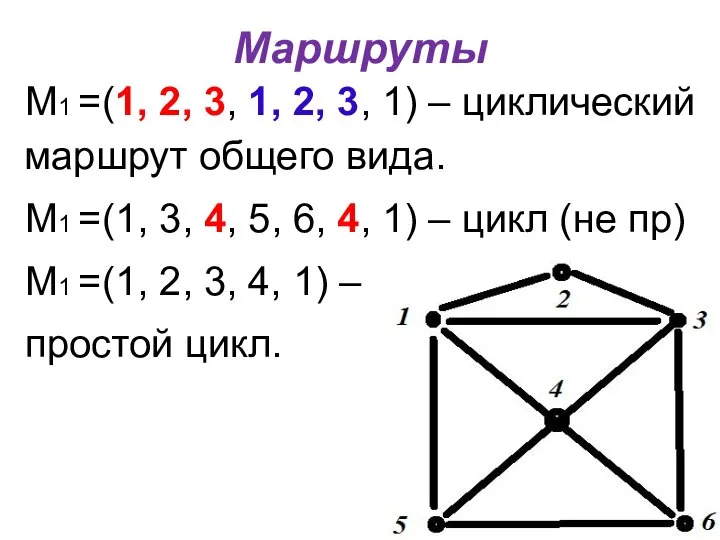
- 8. Маршруты М1 =(1, 2, 3, 1, 2, 3, 1) – циклический маршрут общего вида. М1 =(1,
- 9. Расстояния в графе Расстоянием между вершинами a и b называется длина минимальной простой цепи, связывающей их.
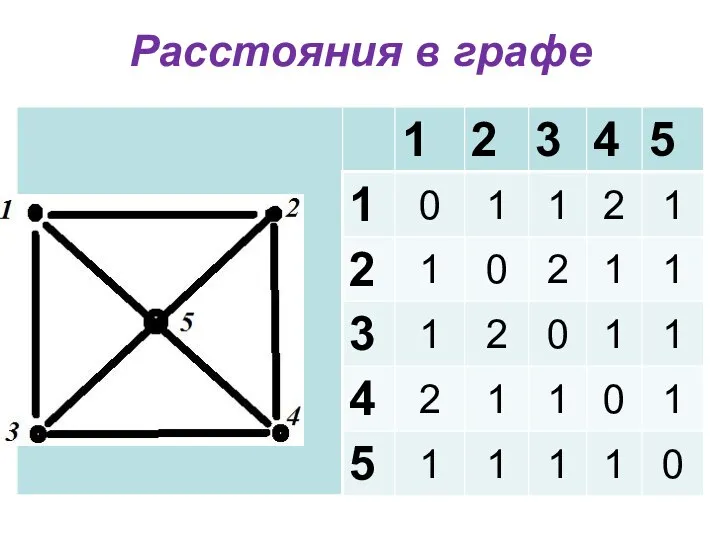
- 10. Расстояния в графе
- 11. Расстояния в графе ri – эксцентриситет i-ой вершины – расстояние от этой вершины до наиболее удаленной
- 12. Расстояния в графе Диаметр графа G – максимальное расстояние между вершинами графа d(G)= max d(vi,vj) по
- 13. Расстояния в графе Центр графа G – это вершина, расстояние от которой до наиболее удаленной вершины
- 14. Расстояния в графе Радиус графа G –расстояние от центра графа до наиболее удаленной вершины. r(G)=min ri
- 15. Расстояния в графе Центр графа G –такая вершина i, для которой ri =r(G). Замечание: Центр в
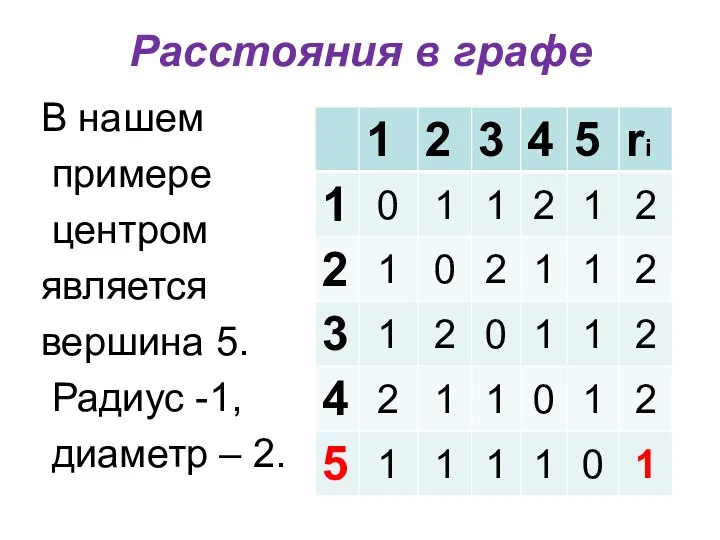
- 16. Расстояния в графе В нашем примере центром является вершина 5. Радиус -1, диаметр – 2.
- 17. Расстояния в графе Диаметральные цепи графа G – простые цепи, длина которых равна d(G), соединяющие наиболее
- 18. Расстояния в графе Радиальные цепи графа G – простые цепи, длина которых равна r(G), соединяющие центр
- 20. Скачать презентацию













 умножение дес др Основное
умножение дес др Основное Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Координатная плоскость. (2). Игра « Морской бой»
Координатная плоскость. (2). Игра « Морской бой» Алгебра и начала анализа. Функции y=sin x и y=cos x, их свойства и графики
Алгебра и начала анализа. Функции y=sin x и y=cos x, их свойства и графики Решение примеров и задач с числами в пределах 10
Решение примеров и задач с числами в пределах 10 Площадь поверхности
Площадь поверхности Решение задач на проценты (%)
Решение задач на проценты (%) Функции и их графики
Функции и их графики Электронный учебник по алгебре для 7 класса
Электронный учебник по алгебре для 7 класса Необходимый признак сходимости
Необходимый признак сходимости Решение комбинаторных задач
Решение комбинаторных задач Неравенство треугольника
Неравенство треугольника Домашняя работа по геометрии, 8 класс
Домашняя работа по геометрии, 8 класс Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 Математика 2 класс. Дидактическая игра «Строим крепость»
Математика 2 класс. Дидактическая игра «Строим крепость» Игра для учащихся «Математический активизатор»
Игра для учащихся «Математический активизатор» Задача Коши и краевая задача для ДУ n-го порядка
Задача Коши и краевая задача для ДУ n-го порядка Математика 5 класс МБОУ СОШ №7 г.Лобня учитель математики Фокина Надежда Николаеевна
Математика 5 класс МБОУ СОШ №7 г.Лобня учитель математики Фокина Надежда Николаеевна  Элементы комбинаторики. Перестановки, размещения, сочетания
Элементы комбинаторики. Перестановки, размещения, сочетания Умножение на двухзначное число
Умножение на двухзначное число Упрощение тригонометрических выражений
Упрощение тригонометрических выражений Функции y = tg x, y = ctg x, их свойства и графики
Функции y = tg x, y = ctg x, их свойства и графики Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки
Векторы. Понятие вектора. Равенство векторов. Откладывание вектора от данной точки Периметр многоугольника
Периметр многоугольника Тест по теме: "Пирамида". Часть 1
Тест по теме: "Пирамида". Часть 1 Активизация мыслительной деятельности учащихся на уроках математики
Активизация мыслительной деятельности учащихся на уроках математики Погрешности результата измерений. Погрешности средств измерений
Погрешности результата измерений. Погрешности средств измерений Решение задач по математике
Решение задач по математике