Содержание
- 2. Математическая статистика Математическая статистика - это раздел прикладной математики, в котором рассматриваются методы отыскания законов и
- 3. Анализ статистических данных включает оценку вероятностей события, функции распределения вероятностей или плотности вероятностей, оценку параметров известного
- 4. Генеральная совокупность Основными понятиями математической статистики являются генеральная совокупность и выборка. Генеральная совокупность – это совокупность
- 5. Генеральная совокупность (продолжение) Не следует смешивать понятие генеральной совокупности с реально существующими совокупностями. Например, на склад
- 6. Выборка Выборкой (выборочной совокупностью) называется совокупность случайно отобранных объектов из генеральной совокупности. Выборка должна быть репрезентативной
- 7. Способы получения выборки: 1) Простой отбор – случайное извлечение объектов из генеральной совокупности с возвратом или
- 8. Ранжирование выборки Полученные различными способами отбора данные образуют выборку. Обычно это множество чисел, расположенных в беспорядке.
- 9. Ранжирование выборки Пример 1. Дана выборка : Проведем ранжирование выборки : После проведения операции ранжирования значения
- 10. Вариационный ряд Вариационный ряд- последовательность вариантов, записанная в возрастающем порядке. Число, показывающее, сколько раз встречаются соответствующие
- 11. Дискретный статистический ряд Дискретным статистическим рядом называется ранжированная совокупность вариантов (хi) с соответствующими им частотами (ni)
- 12. Характеристики дискретного статистического ряда: Размах варьирования R= Мода ( ) – вариант , имеющий наибольшую частоту
- 13. Если изучаемая случайная величина Х является непрерывной или число значений её велико, то составляют интервальный статистический
- 14. Более точно шаг можно рассчитать с помощью формулы Стерджеса: , число интервалов m ≈ 1+ 3,322*lg
- 15. За начало первого интервала рекомендуется брать величину , а конец последнего должен удовлетворять условию: . Промежуточные
- 16. В первую строку таблицы статистического распределения вписывают частичные промежутки: Во вторую строку статистического ряда вписывают количество
- 17. Эмпирическая функция распределения. Пусть получено статистическое распределение выборки, и каждому варианту из этой выборки поставлена в
- 18. Функция F*(х) обладает теми же свойствами, что и функция F(x): 1. 2. F*(x) – неубывающая функция
- 19. Эмпирическая плотность распределения Для интегральной функции распределения F(x) справедливо приближённое равенство: , где f(x) –дифференциальная функция
- 20. Пусть наблюдаемые значения непрерывной случайной величины представлены в виде интервального вариационного ряда. Полагая, что - частость
- 21. Графическое изображение статистических данных. Статистическое распределение изображается графически с помощью полигона и гистограммы. Полигоном частот называют
- 22. Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основания которых расположены на оси Ох и
- 23. Пример 1. Дана выборка значений случайной величины Х объёма 20: 12, 14, 19, 15, 14, 18,
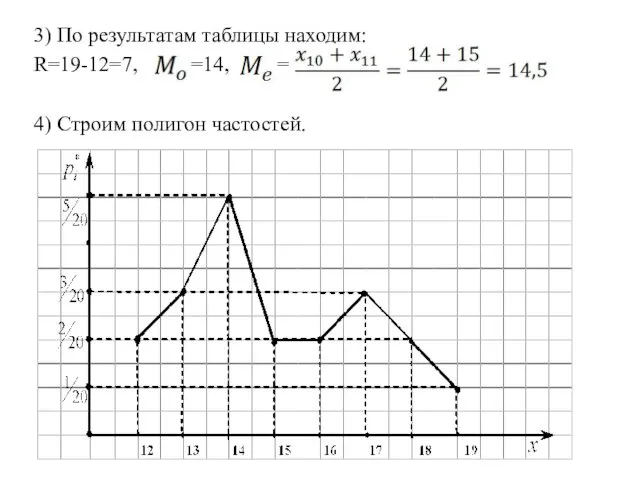
- 24. 3) По результатам таблицы находим: R=19-12=7, =14, = 4) Строим полигон частостей.
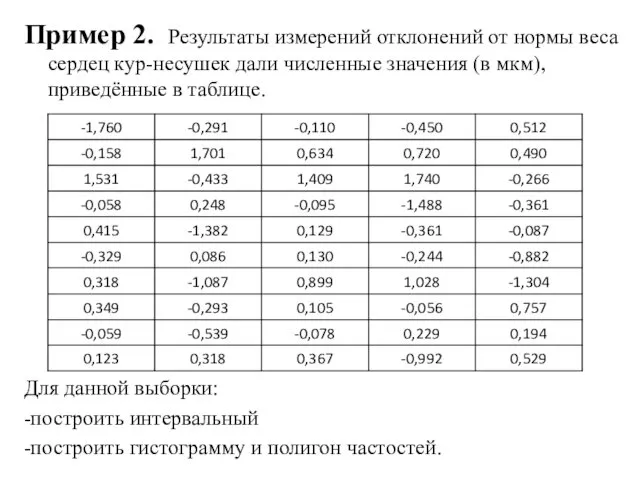
- 25. Пример 2. Результаты измерений отклонений от нормы веса сердец кур-несушек дали численные значения (в мкм), приведённые
- 26. 1) Строим интервальный ряд. По данным таблицы определяем хmin= -1,76 xmax=1,74; Для определения длины интервала h
- 27. Строим интервальный ряд:
- 29. Скачать презентацию
























 5-6 классы
5-6 классы Наибольший общий делитель
Наибольший общий делитель Теория графов
Теория графов Длина окружности и площадь круга
Длина окружности и площадь круга Презентация по математике "Решение диофантовых уравнений" - скачать
Презентация по математике "Решение диофантовых уравнений" - скачать  Простые и составные числа
Простые и составные числа Стандартный вид числа
Стандартный вид числа Исследование лабиринтов
Исследование лабиринтов Простые числа. Решето Эратосфена
Простые числа. Решето Эратосфена Обзор численных методов
Обзор численных методов Степень с натуральным показателем и ее свойства
Степень с натуральным показателем и ее свойства Весёлая математика
Весёлая математика Тела вращения
Тела вращения Лесная школа. Умножение и деление. Задачи в стихах
Лесная школа. Умножение и деление. Задачи в стихах Тема урока: «Умножение и деление десятичных дробей на натуральные числа»
Тема урока: «Умножение и деление десятичных дробей на натуральные числа» VIII Международная олимпиада по математике для I курсов ССУЗ
VIII Международная олимпиада по математике для I курсов ССУЗ Значения выражений
Значения выражений Основное свойство дроби. Сокращение дробей
Основное свойство дроби. Сокращение дробей Школа № 254 Преподаватель Павлова Марина Константиновна
Школа № 254 Преподаватель Павлова Марина Константиновна  Загадкове число. Число пі
Загадкове число. Число пі Решение заданий ЕГЭ. Элементы комбинаторики, статистики и теории вероятностей
Решение заданий ЕГЭ. Элементы комбинаторики, статистики и теории вероятностей Описательная статистика
Описательная статистика Сращивание асимптотических разложений. Логарифмы. (Лекция 7)
Сращивание асимптотических разложений. Логарифмы. (Лекция 7) Презентация по математике "Бенефис дробей" - скачать
Презентация по математике "Бенефис дробей" - скачать  Табличное умножение и деление. 2 класс
Табличное умножение и деление. 2 класс Несобственные интегралы
Несобственные интегралы Производная функции в точке
Производная функции в точке Решение неравенств второй степени
Решение неравенств второй степени