Содержание
- 2. 1. Теория и практика приближенных вычислений
- 3. 08.09.2016 Вопросы: Абсолютная и относительная погрешности Верные значащие цифры Правила округления чисел и погрешностей
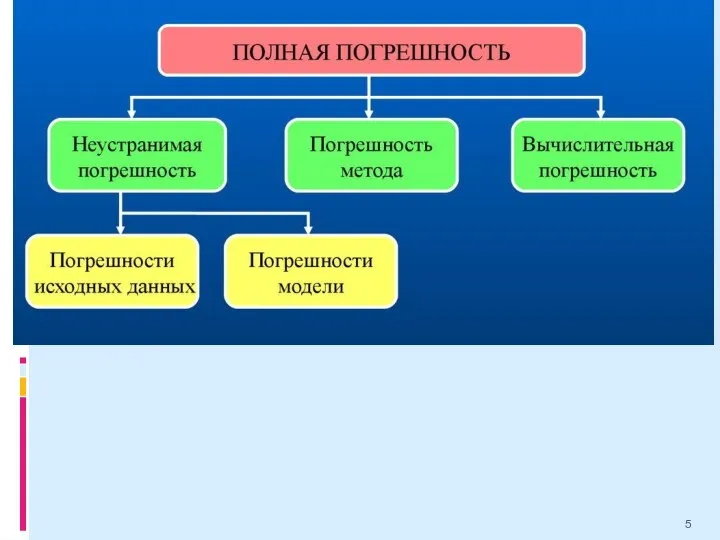
- 4. ВВЕДЕНИЕ Под погрешностью понимается величина, характеризующая точность результата. Выделяют три основных вида погрешностей: 1. Неустранимая погрешность
- 6. 1. Абсолютная и относительная погрешности Пусть Х – точное значение некоторой величины, а х – ее
- 7. Абсолютной относительной погрешностью приближенного числа х называется отношение Абсолютная и относительная погрешности связаны соотношением Относительную погрешность
- 8. 2. Значащие цифры Первая слева, отличная от нуля цифра данного числа и все следующие за ней
- 9. Погрешность Δх подбирают так, чтобы : а) в записи Δх было не более 1 – 3
- 10. Верные значащие цифры 2.1. Значащая цифра числа называется верной в строгом (узком) смысле, если абсолютная погрешность
- 11. 6: стоит в разряде единиц, ½=0,5>0,007 - верная 8: стоит в разряде десятых, 0,1/2=0,05>0,007 - верная
- 12. 2.2. Значащая цифра числа называется верной в широком смысле, если абсолютная погрешность числа не превосходит единицы
- 13. 3. Правила округления чисел и погрешностей 3.1. При записи чисел руководствуются правилом: все значащие цифры должны
- 14. Примеры. Округлить числа до сотых: 1) 1,2537≈1,25; 2) 1,2563≈1,26,; 3) 2,36566≈2,37; 4) 2,665≈2,66,(т.к. 6 – четная);
- 15. Погрешность округления Пример. Пусть в приближенном значении а=16,395 все цифры верны в широком смысле. Округлим а
- 16. 3.2. Правила округления погрешностей Пример. Округлить до сотых число 4,5371±0,0482 Сначала округлим погрешность , оставив одну
- 17. 15.09.2016 Прямая задача теории погрешностей Вопросы: Учет погрешности приближенных вычислений. Систематический учет погрешностей при вычислениях Метод
- 18. Прямая задача теории погрешностей: Заключается в том, чтобы оценить погрешность вычисления значений функции по заданной погрешности
- 19. 1. Учет погрешности приближенных вычислений 1.1. Строгие методы оценки точности результатов вычислений: Систематический пооперационный учёт погрешностей;
- 20. Погрешность результатов арифметических операций Относительная погрешность алгебраической суммы равна Пусть известны погрешности Δх и Δу соответственно
- 21. Предельная относительная погрешность произведения (частного) равна сумме относительных погрешностей слагаемых (делимого и делителя). Предельные абсолютные погрешности
- 22. Пример 1. а) Записать порядок выполняемых операций, оценить погрешности их результатов, вычислить и оценить погрешность искомого
- 23. Предельная относительная погрешность операций возведения в степень и извлечения корня. Предельные абсолютные погрешности вычисляется по формулам
- 24. Погрешность вычисления функции Пусть задана дифференцируемая функция и абсолютные погрешности аргументов Тогда абсолютная погрешность функции вычисляется
- 25. Пример 2. а) Записать порядок выполняемых операций, оценить погрешности их результатов, вычислить и оценить погрешность искомого
- 26. Пример 3. Δπ=0,0016
- 28. Пример 4. а) Записать порядок выполняемых операций, оценить погрешности их результатов, вычислить и оценить погрешность искомого
- 29. Порядок выполняемых операций:
- 30. б) Для определения числа верных знаков воспользуемся определением и оценкой для абсолютной погрешности функции. Таким образом,
- 31. Метод границ
- 32. Метод границ
- 33. Оценить точность вычислений методом границ НГ(a-b)=НГа – ВГb = 9,20 – 3,07=6,13 ВГ(a-b)=ВГа – НГb =
- 35. Метод подсчета верных цифр – нестрогий метод оценки точности вычислений
- 38. 5. Обратная задача теории погрешностей Необходимо определить допустимую погрешность аргументов по допустимой погрешности функции. Для функции
- 39. Пример (обратная задача) Выяснить погрешность задания исходных данных, необходимую для получения результата с верными значащими цифрами.
- 40. Исходим из того, что Для использования принципа равных влияний считаем, что все слагаемые , равны между
- 42. Скачать презентацию






































 Деление десятичных дробей
Деление десятичных дробей Разложение на множители с помощью группировки
Разложение на множители с помощью группировки 20180329_urok_6_klass-_1a
20180329_urok_6_klass-_1a Плоскость. Прямая. Луч
Плоскость. Прямая. Луч Свойства логарифмов
Свойства логарифмов Четырёхзначные таблицы В.М. Брадиса
Четырёхзначные таблицы В.М. Брадиса Презентация Сравнение многозначных чисел
Презентация Сравнение многозначных чисел  Основное свойство дроби
Основное свойство дроби Комплексные числа. Решение двучленного уравнения
Комплексные числа. Решение двучленного уравнения Побудова розгорток геометричних фігур
Побудова розгорток геометричних фігур Кружок «Математика на свежем воздухе»
Кружок «Математика на свежем воздухе» Объем тел
Объем тел Применение распределительного свойства умножения 6 класс
Применение распределительного свойства умножения 6 класс  Диаграммы рассеивания
Диаграммы рассеивания Домашнее задание. Геометрия
Домашнее задание. Геометрия Проценты в современной жизни
Проценты в современной жизни Предмет теории систем
Предмет теории систем Натуральные числа и суеверия, связанные с ними
Натуральные числа и суеверия, связанные с ними Показательные уравнения и неравенства
Показательные уравнения и неравенства Старинная задача по математике
Старинная задача по математике Аттестационная работа. Образовательная программа дополнительного образования Избранные вопросы математики. (6 класс)
Аттестационная работа. Образовательная программа дополнительного образования Избранные вопросы математики. (6 класс) Призмы. Виды призм
Призмы. Виды призм Математика в моей будущей профессии. Подготовила Подшибякина Наталья, учащаяся 10 «А» класса. Руководитель: Иващенко Ольга Иван
Математика в моей будущей профессии. Подготовила Подшибякина Наталья, учащаяся 10 «А» класса. Руководитель: Иващенко Ольга Иван Викторина «Своя игра». (10 класс)
Викторина «Своя игра». (10 класс) Решение уравнения. (Задание 13)
Решение уравнения. (Задание 13) Одночлены и многочлены
Одночлены и многочлены Решение задач с помощью уравнений (5 класс)
Решение задач с помощью уравнений (5 класс) Визначений інтеграл
Визначений інтеграл