Содержание
- 2. Якщо функція f(x) неперервна на відрізку [a;b](де a Розбити цей відрізок на n частинних відрізків довжиною
- 3. Означення Якщо по різному ділити відрізок [a;b] на n частинних відрізків і по-різному вибирати на них
- 4. Властивості визначеного інтеграла 1) При перестановці меж інтегрування знак інтегралу змінюється на протилежний: 2) Інтеграл з
- 5. 5) Постійний множник k можна виносити за знак інтеграла: Для обчислення визначеного інтеграла використовується формула Ньютона-Лейбніца:
- 6. Приклад 1. Приклад 2.
- 7. 2. Метод заміни змінної у визначеному інтегралі. Якщо визначений інтеграл перетворюється за допомогою підстановки: в інший
- 8. Приклад 3.
- 9. Інтегрування частинами у визначеному інтегралі. Якщо підінтегральний вираз у визначеному інтегралі можна представити у вигляді добутку
- 10. Приклад 4.
- 11. 3. Невласні інтеграли. а) Інтеграли з нескінченними межами. Означення. Якщо існує скінченна границя: то цю границю
- 12. Тобто: (3) У цьому випадку кажуть, що інтеграл існує або він є збіжним. Якщо не має
- 13. Приклад. Обчислити інтеграл: Розв’язок:
- 14. б) Інтеграли від розривних функцій. Якщо функція визначена та неперервна у відкритому інтервалі: ,а у точці
- 16. Скачать презентацию

![Означення Якщо по різному ділити відрізок [a;b] на n частинних відрізків](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1470232/slide-2.jpg)


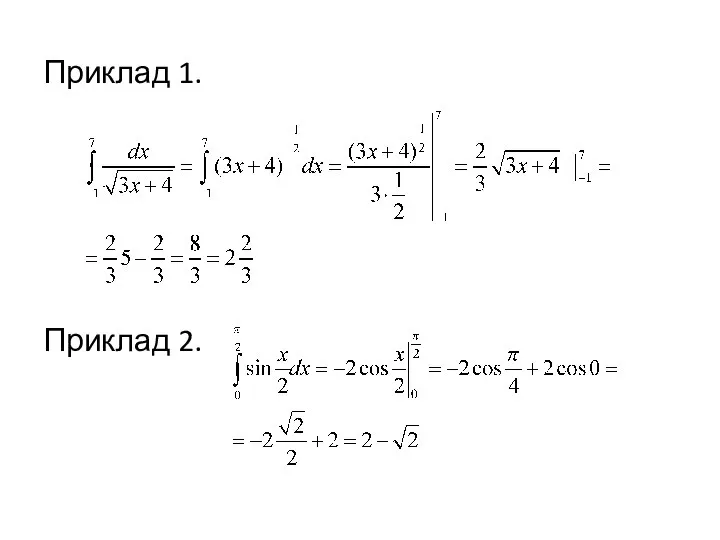

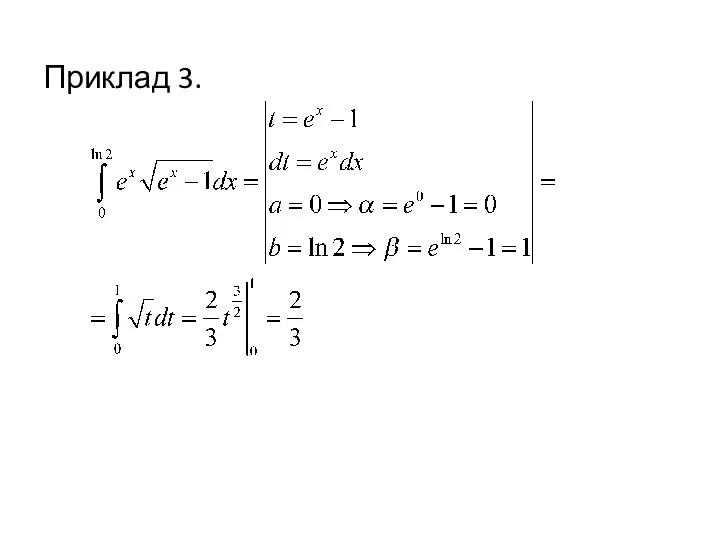






 Свойства прямоугольных треугольников
Свойства прямоугольных треугольников Тема: Внетабличное умножение и деление. Развивать навык в решении примеров на внетабличное умножение и деление; Повторять прой
Тема: Внетабличное умножение и деление. Развивать навык в решении примеров на внетабличное умножение и деление; Повторять прой Сложение и вычитание смешанных чисел. 5 класс
Сложение и вычитание смешанных чисел. 5 класс Матрицы и определители
Матрицы и определители Практика. Примеры решения задач по темам: предел функции, вычисление производных, исследование функции
Практика. Примеры решения задач по темам: предел функции, вычисление производных, исследование функции Геометрические тела и их проекции
Геометрические тела и их проекции Прямая пропорциональная зависимость
Прямая пропорциональная зависимость Осевая и центральная симметрии
Осевая и центральная симметрии Introduction to Statistics. Week 1 (2)
Introduction to Statistics. Week 1 (2) Понятие вектора в пространстве
Понятие вектора в пространстве Правильные многогранники
Правильные многогранники Операция двоичного сложения и её свойства. Многочлен Жегалкина
Операция двоичного сложения и её свойства. Многочлен Жегалкина Производная и дифференциал. Производные высших порядков
Производная и дифференциал. Производные высших порядков Треугольник и его виды
Треугольник и его виды Применение интегралов для решения физических задач
Применение интегралов для решения физических задач Площадь трапеции (От простого к сложному)
Площадь трапеции (От простого к сложному) Счастливый случай. 7 класс
Счастливый случай. 7 класс Линейная функция у=кх
Линейная функция у=кх Параллельность плоскостей
Параллельность плоскостей Свойства функции
Свойства функции История возникновения счёта, появление цифр и систем счисления
История возникновения счёта, появление цифр и систем счисления Вводный урок по теме "Элементы математической статистики"
Вводный урок по теме "Элементы математической статистики"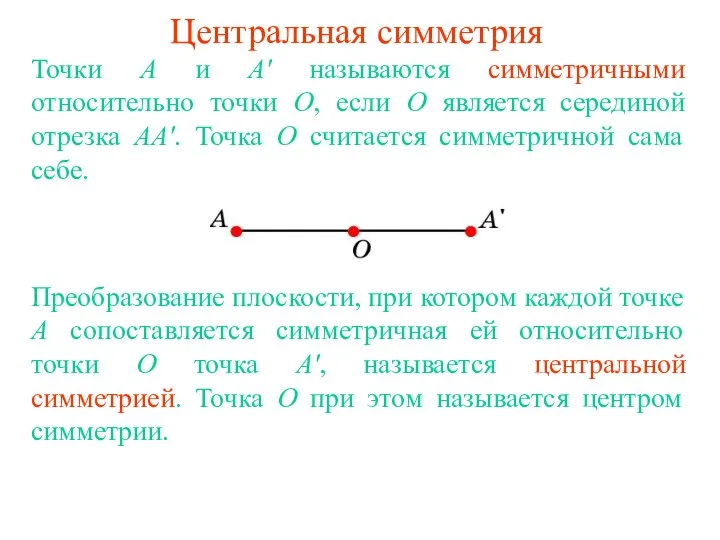 Центральная симметрия
Центральная симметрия Показательная функция
Показательная функция Общее повторение алгебры
Общее повторение алгебры Усечённая пирамида
Усечённая пирамида Нам радостно, нам весело! Смеемся мы с утра. Но вот пришло мгновенье, Серьезным быть пора. Глазки прикрыли, ручки сложили, Головки
Нам радостно, нам весело! Смеемся мы с утра. Но вот пришло мгновенье, Серьезным быть пора. Глазки прикрыли, ручки сложили, Головки  Урок математики в 6 «в» классе «Алгоритм решения задач на пропорции» Учитель: Лиманская Ю. И МОУ СОШ №11
Урок математики в 6 «в» классе «Алгоритм решения задач на пропорции» Учитель: Лиманская Ю. И МОУ СОШ №11