Содержание
- 2. Высказыванием называют любое повествовательное предложение, о котором можно сказать, истинно оно или ложно. Высказывания и предикаты
- 3. «Истина» и «ложь» называются значениями истинности высказывания. Каждое высказывание либо истинно, либо ложно, быть одновременно тем
- 4. Существуют предложения, относительно которых без дополнительных условий нельзя установить, истинно оно или ложно. Такие предложения называются
- 5. Два высказывания А и В равносильны (эквивалентны), если они одновременно истинны или одновременно ложны: А =
- 6. Предикатом называется предложение с одной или несколькими переменными, обращающееся в высказывание всякий раз при подстановке вместо
- 8. Вместе с предикатом, как правило, задается и множество, из которого выбираются значения переменной (переменных), входящей в
- 9. Множество значений переменной, которые обращают предикат в истинное высказывание, называется множеством истинности предиката. Примеры: 1) А(х):«х
- 10. 3) D(х): «х у» х, у ∈ Х, где Х - множество однозначных четных натуральных
- 11. Предложение называется простым (элементарным), если никакая его часть сама не является предложением. Предложение называется составным, если
- 12. Примеры: 1) Число 28 четное и делится на 7. 2) Число х меньше или равно 7.
- 13. Упражнение Среди следующих предложений укажите высказывания и предикаты. Для высказываний укажите значения истинности, для предикатов –
- 14. Операции над высказываниями и предикатами Отрицание Отрицание некоторого высказывания А можно получить, если перед данным высказыванием
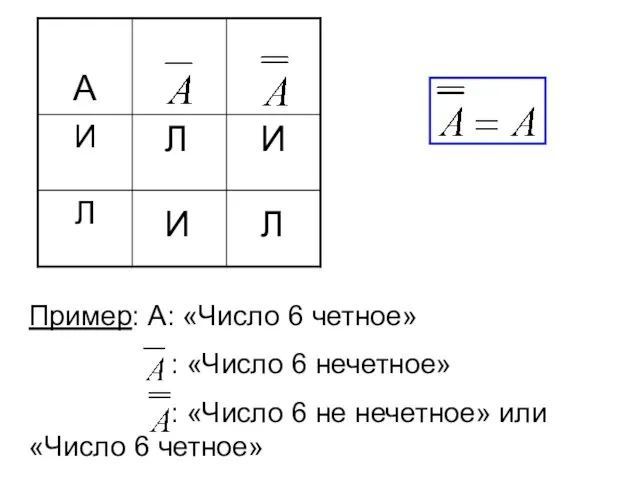
- 15. Отрицанием высказывания А называется такое высказывание Ā, которое истинно, если данное высказывание ложно, и ложно, если
- 16. И И Л Л Пример: А: «Число 6 четное» : «Число 6 нечетное» : «Число 6
- 17. Отрицанием предиката А(х), заданного на множестве Х, называют предикат Ā(х), определенный на том же множестве Х,
- 18. Пример: Х = {10, 15, 20, 25, 30} А(х): «Число х оканчивается цифрой 5» Ā(х): «Неверно,
- 19. Упражнения 1. Образуйте отрицание каждого из следующих высказываний; укажите, является истинным данное высказывание или его отрицание.
- 20. Логическая операция, в результате которой из двух высказываний А и В с помощью логической связки «и»
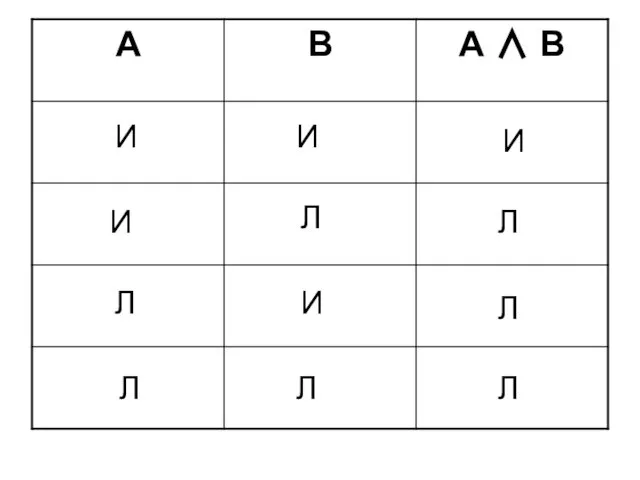
- 21. Конъюнкция двух высказываний А и В - это такое высказывание А∧В, которое истинно тогда и только
- 22. И И И Л Л И Л Л Л Л Л И
- 23. Примеры: А: «15 3», В: «15 5», А ∧ В: «Число 15 кратно 3
- 24. 3) 3 А: «3 Двойное числовое неравенство представляет собой конъюнкцию двух неравенств
- 25. И Л Л Л
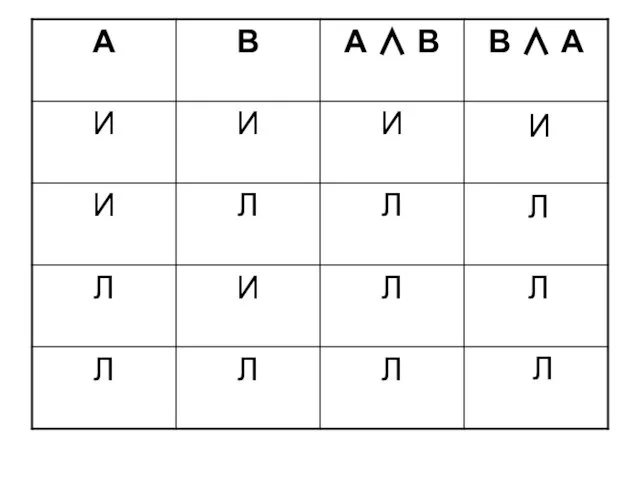
- 26. А ∧ В = В ∧ А коммутативный закон конъюнкции Пример: А ∧ В: «Число 12
- 27. И И Л Л Л Л Л Л И Л Л Л Л Л Л Л
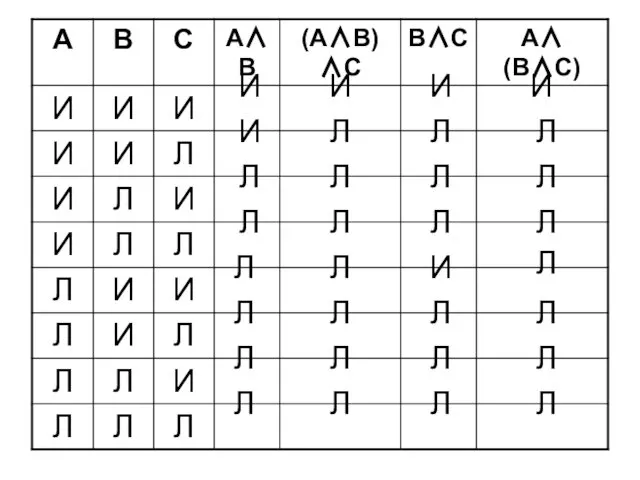
- 28. (А ∧ В) ∧ С = А ∧ (В ∧ С) ассоциативный закон конъюнкции
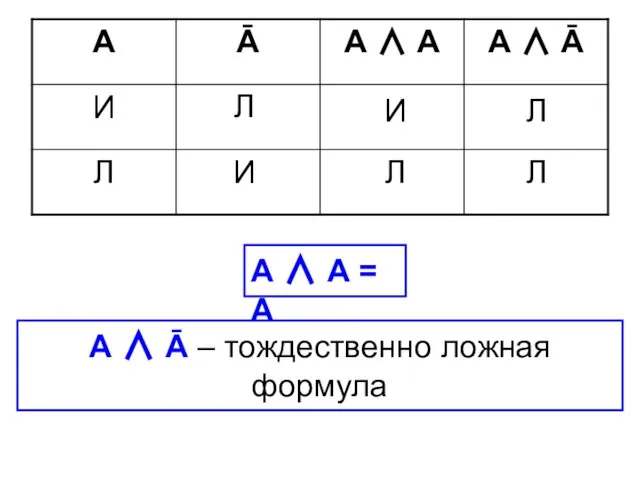
- 29. Л Л Л Л И И А ∧ А = А А ∧ Ā – тождественно
- 30. Замечание: В обыденной речи конъюнкция может выражаться с помощью различных союзов: «и», «а», «но», «не только…,
- 31. Конъюнкцией предикатов А(х) и В(х), заданных на множестве Х, называется предикат А(х)∧В(х), заданный на том же
- 32. Пример: А(х): «Число х четное», В(х): «Число х кратно 5», х∈Х, Х = {10, 15, 16,
- 33. Дизъюнкция Логическая операция, в результате которой из двух высказываний А и В с помощью логической связки
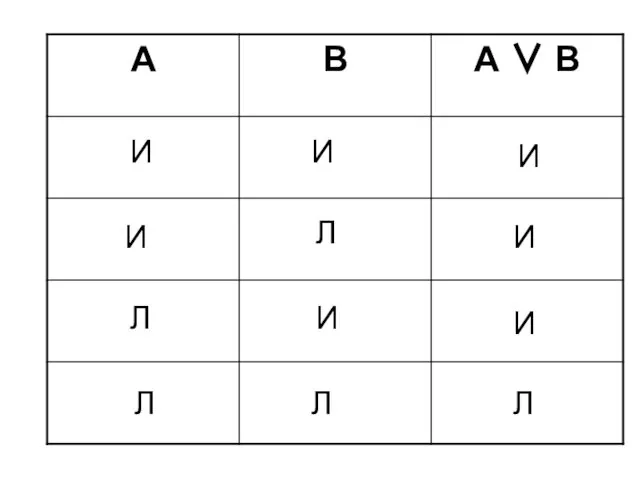
- 34. Дизъюнкция двух высказываний А и В - это такое высказывание А ∨ В, которое истинно тогда
- 35. И И И Л Л И Л Л Л И И И
- 36. Замечание: В обыденной речи союз «или» употребляется в двух смыслах: как разделительный или неразделительный. Примеры: 1)
- 37. Примеры: 1) А: «10 > 7» (И), В: «10 = 7» (Л), А ∨ В: «10
- 38. И И И Л
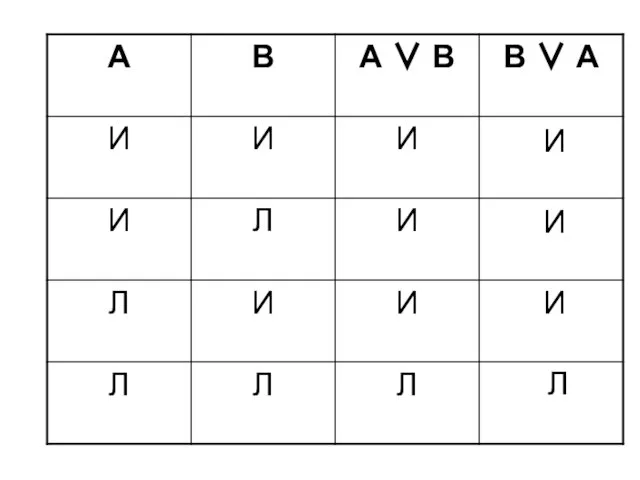
- 39. А ∨ В = В ∨ А коммутативный закон дизъюнкции
- 40. И И И И И И Л Л И И И И И И И Л
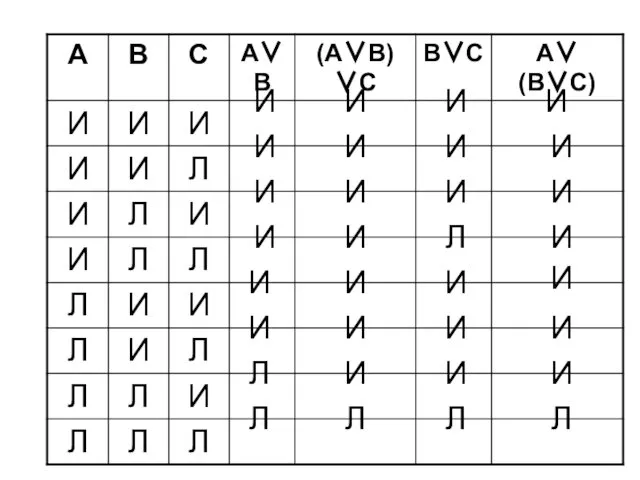
- 41. (А ∨ В) ∨ С = А ∨ (В ∨ С) ассоциативный закон дизъюнкции (А ∧
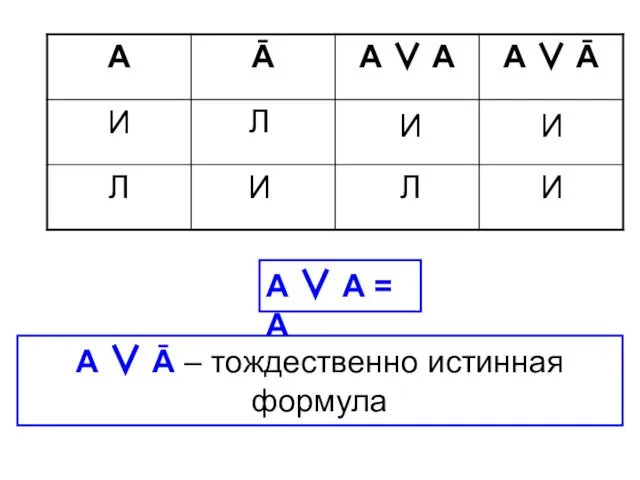
- 42. Л И И Л И И А ∨ А = А А ∨ Ā – тождественно
- 43. Дизъюнкцией предикатов А(х) и В(х), заданных на множестве Х, называется предикат А(х)∨В(х), заданный на том же
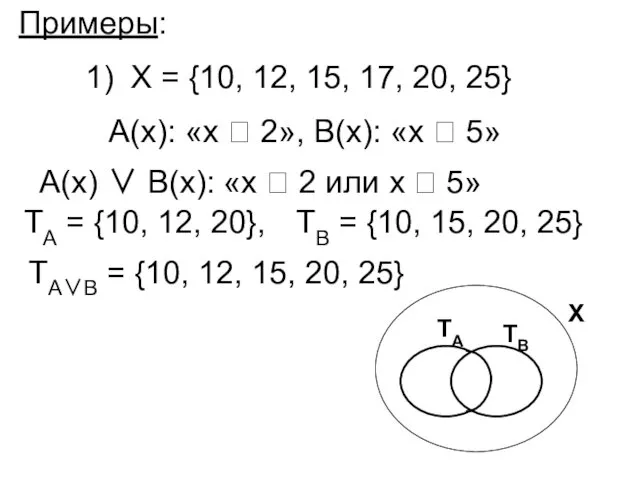
- 44. Примеры: Х = {10, 12, 15, 17, 20, 25} А(х): «х 2», В(х): «х
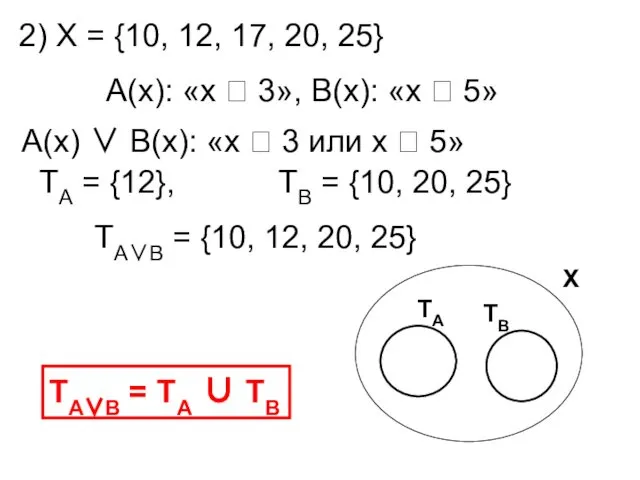
- 45. 2) Х = {10, 12, 17, 20, 25} А(х): «х 3», В(х): «х 5»
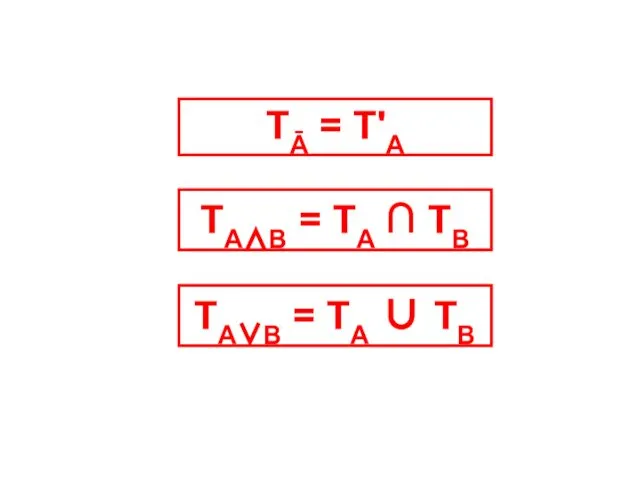
- 46. ТА∨В = ТА ∪ ТВ ТА∧В = ТА ∩ ТВ ТĀ = Т'А
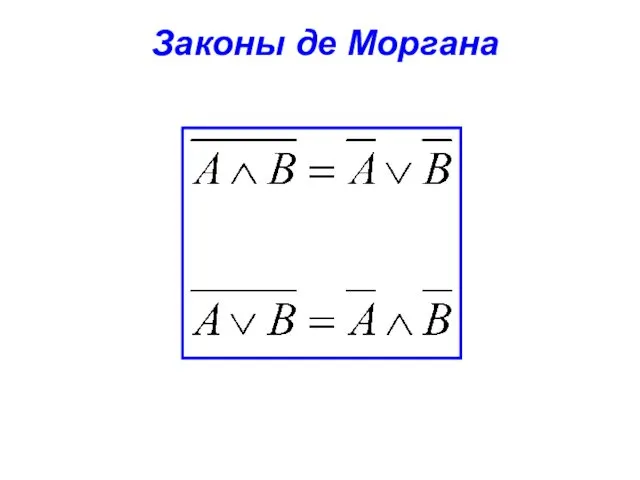
- 47. Законы де Моргана
- 48. Доказательство Л Л И И Л И И Л И Л Л Л Л Л И
- 49. Пример: А: «Я играю в шахматы», В: «Я играю в шашки». А∨В: «Я играю в шахматы
- 50. Упражнения Известно, что высказывание А – истинно. Можно ли, зная лишь это определить значение истинности высказывания:
- 51. 3) Покажите, что выполняя следующие задания, мы находим множество истинности конъюнкции и дизъюнкции предикатов: а) Даны
- 52. Решение задач на распознавание объектов Решение задач на распознавание объектов связано с понятиями конъюнкции и дизъюнкции.
- 53. Алгоритм распознавания 1. Проверить, истинно ли высказывание: х ∈ С. 2. Если х ∉ С, то
- 54. Если видовое отличие представляет собой конъюнкцию свойств, т.е. Р = Р1 ∧ Р2 ∧ … ∧
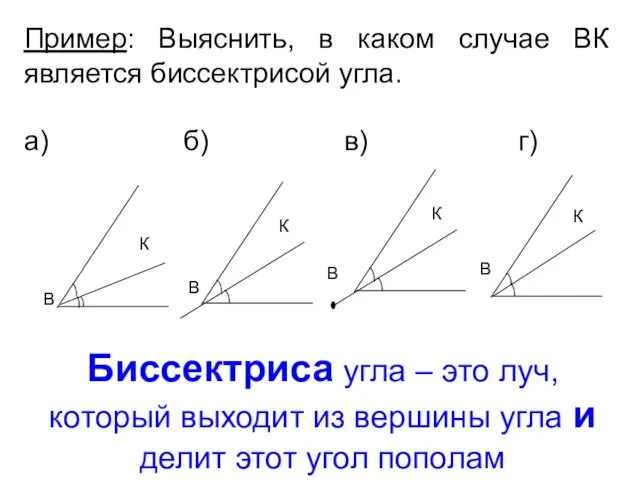
- 55. Пример: Выяснить, в каком случае ВК является биссектрисой угла. а) б) в) г) Биссектриса угла –
- 56. Если видовое отличие представляет собой дизъюнкцию свойств: Р = Р1 ∨ Р2 ∨ … ∨ Рк,
- 57. Пример: Даны множества А={1, 2, 3}, В={2, 4, 6}. Какие из чисел 1, 2, 3, 4,
- 58. Импликация Составное высказывание, которое образовано из двух элементарных высказываний с помощью логической связки «если …, то…»,
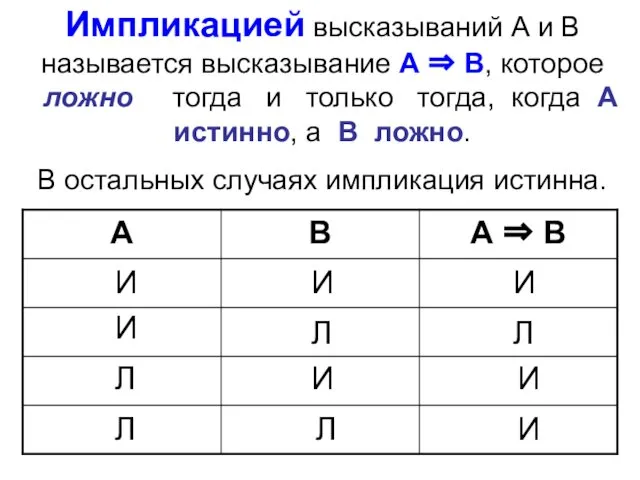
- 59. Импликацией высказываний А и В называется высказывание А ⇒ В, которое ложно тогда и только тогда,
- 60. Пример: А: «Треугольник АВС прямоугольный» В: «В треугольнике АВС квадрат одной стороны равен сумме квадратов двух
- 61. 1) «Если Наполеон – француз, то 2·2 = 4». 2) «Если 2 · 2 = 5,
- 62. Замечание: Употребление слов «Если…, то…» в логике отличается от употребления их в обыденной речи, где мы
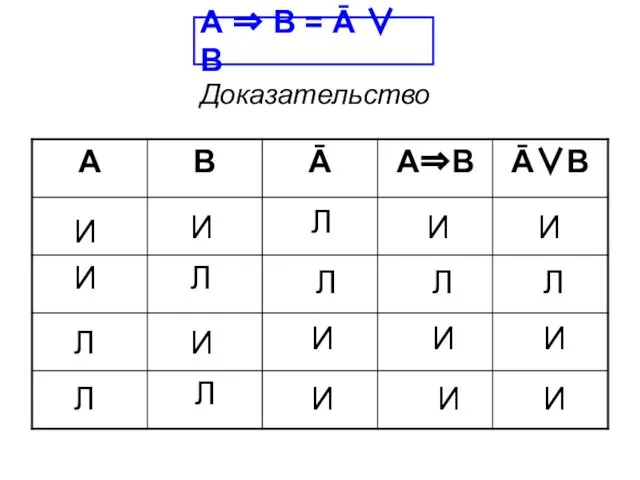
- 63. А ⇒ В = Ā ∨ В Доказательство И И И Л И Л Л Л
- 64. А ⇒ В – данная импликация В ⇒ А - импликация обратная данной - импликация противоположная
- 65. А ⇒ В: «Если сумма цифр числа 126 кратна 3, то и само число 126 кратно
- 66. А ⇒ В = Ā ∨ В Отрицание импликации
- 67. Импликацией предикатов А(х) и В(х), заданных на множестве Х, называется предикат А(х)⇒В(х), заданный на том же
- 68. Примеры: 1) А(х): «Число х кратно 3» и В(х): «Число х –двузначное», х ∈ N А(х)⇒В(х):
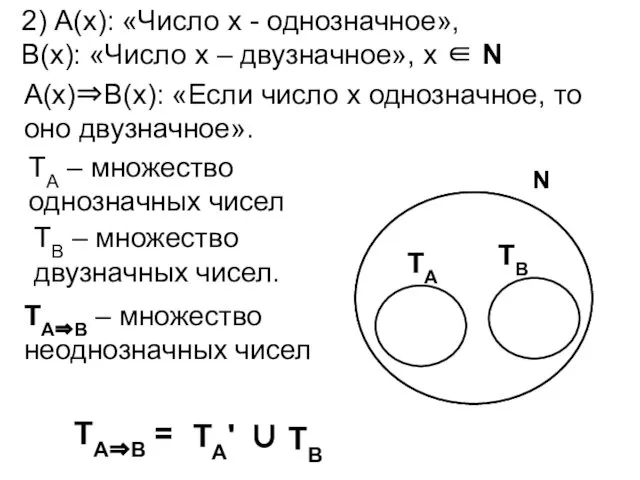
- 69. 2) А(х): «Число х - однозначное», В(х): «Число х – двузначное», х ∈ N А(х)⇒В(х): «Если
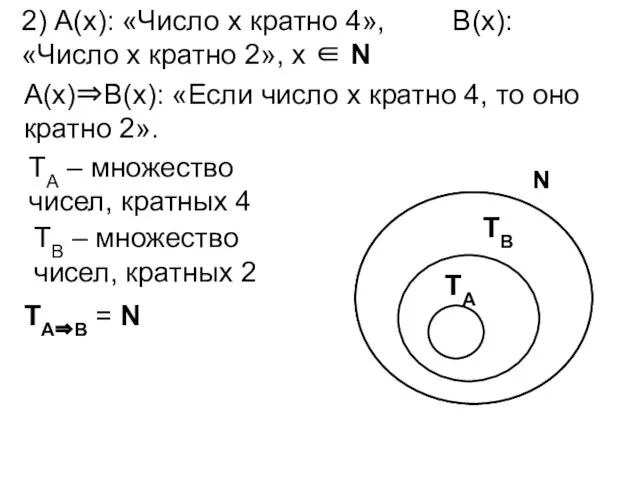
- 70. 2) А(х): «Число х кратно 4», В(х): «Число х кратно 2», х ∈ N А(х)⇒В(х): «Если
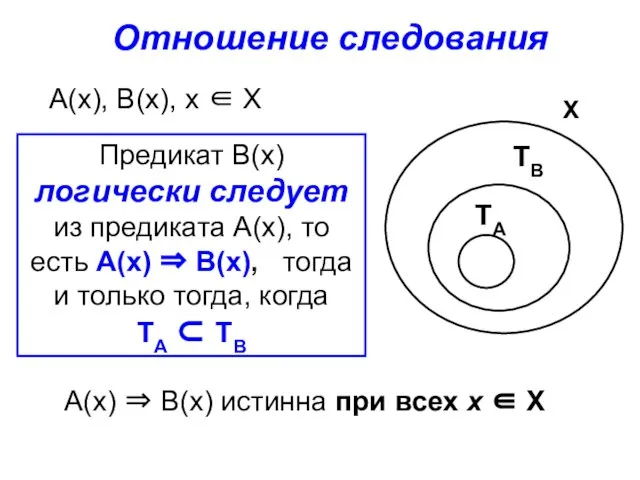
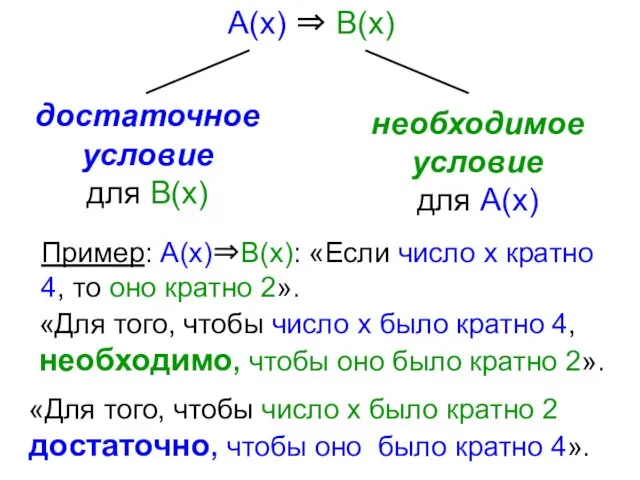
- 71. Отношение следования А(х), В(х), х ∈ Х А(х) ⇒ В(х) истинна при всех х ∈ Х
- 72. Пример: А(х)⇒В(х): «Если число х кратно 4, то оно кратно 2». «Для того, чтобы число х
- 73. Эквиваленция Составное высказывание, которое образовано из двух элементарных высказываний с помощью логических связок «если и только
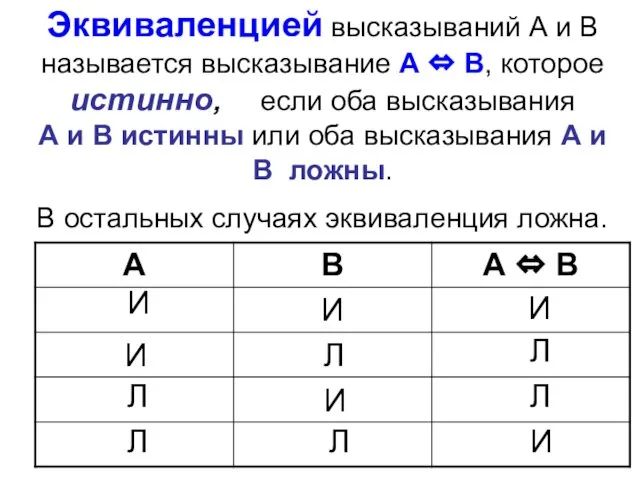
- 74. Эквиваленцией высказываний А и В называется высказывание А ⇔ В, которое истинно, если оба высказывания А
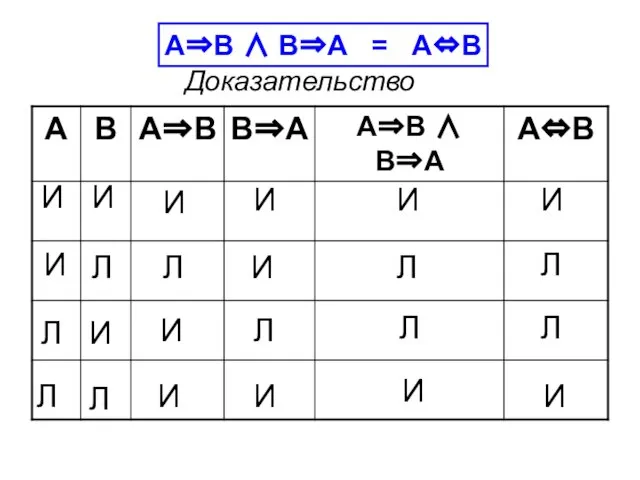
- 75. А⇒В ∧ В⇒А = А⇔В Доказательство И Л И И И Л Л И Л И
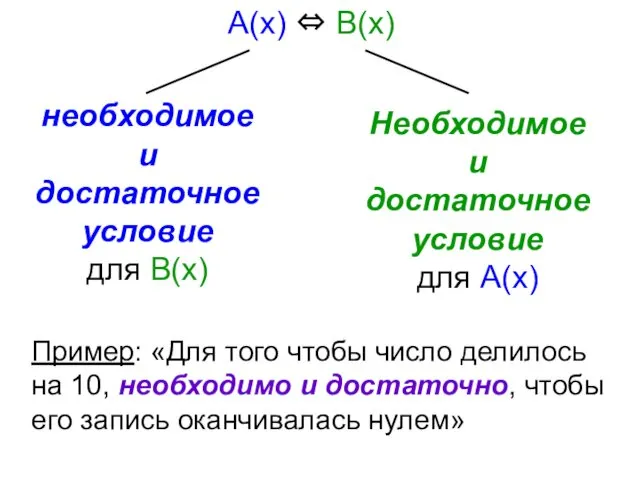
- 76. Эквиваленцией предикатов А(х) и В(х), заданных на множестве Х, называется предикат А(х)⇔В(х), заданный на том же
- 77. Если предикаты А(х) и В(х) равносильны на множестве Х, то эквиваленция предикатов А(х) ⇔ В(х) истинна
- 78. Пример: А(х) «Число х делится на 10», В(х): «Запись числа х заканчивается цифрой 0» А(х)⇔В(х): «Число
- 79. Пример: «Для того чтобы число делилось на 10, необходимо и достаточно, чтобы его запись оканчивалась нулем»
- 80. Замечание. Из равносильности предикатов А(х) и В(х) на некотором множестве Х не следует, что предикаты, выраженные
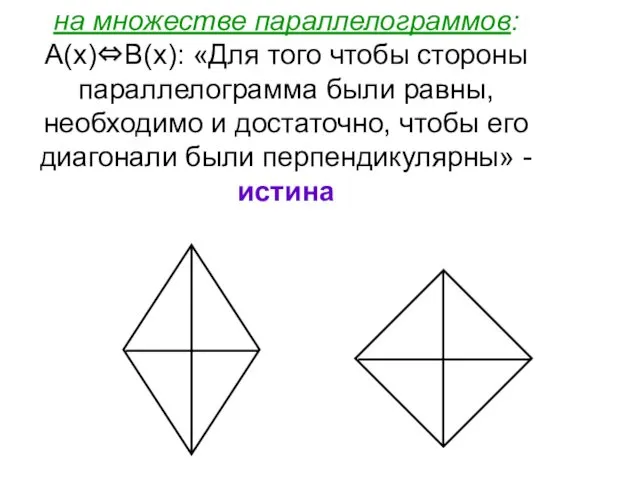
- 81. на множестве параллелограммов: А(х)⇔В(х): «Для того чтобы стороны параллелограмма были равны, необходимо и достаточно, чтобы его
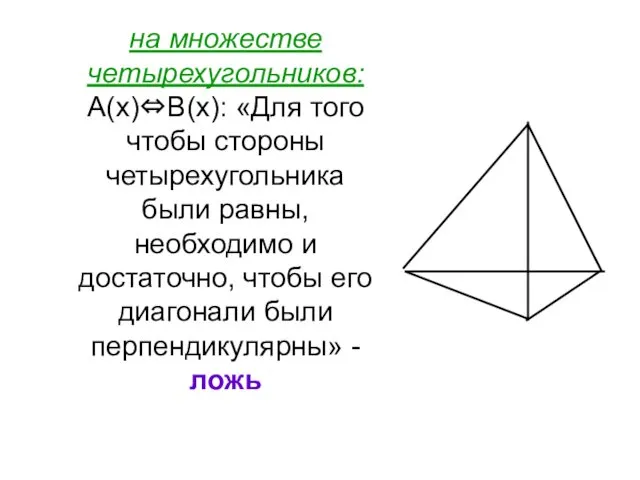
- 82. на множестве четырехугольников: А(х)⇔В(х): «Для того чтобы стороны четырехугольника были равны, необходимо и достаточно, чтобы его
- 84. Скачать презентацию


















































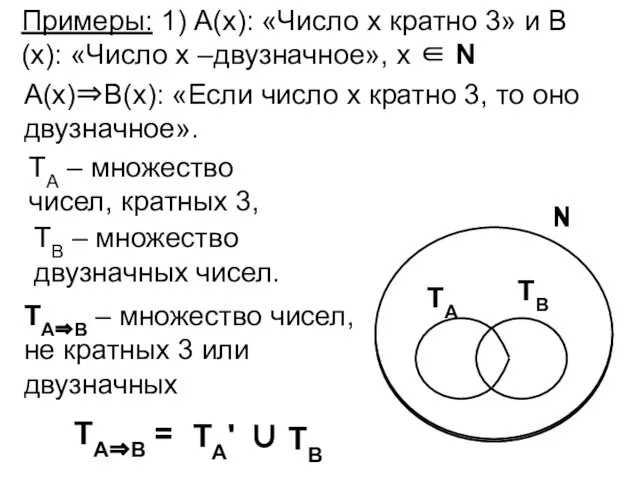





 Знаки тригонометрических функций
Знаки тригонометрических функций Figures of matching
Figures of matching Тренажер для устного счета «Свойства степени с целым показателем»
Тренажер для устного счета «Свойства степени с целым показателем» Урок математики. Запись чисел римскими цифрами
Урок математики. Запись чисел римскими цифрами Единицы площади. Ар. Гектар
Единицы площади. Ар. Гектар Вычисление определителя третьего порядка по правилу треугольников
Вычисление определителя третьего порядка по правилу треугольников Подготовка к ОГЭ. Задания по геометрии. Занятие 7
Подготовка к ОГЭ. Задания по геометрии. Занятие 7 Задачи на построение угла. Биссектриса
Задачи на построение угла. Биссектриса Стереометрия аксиомалары
Стереометрия аксиомалары Логарифмическая функция
Логарифмическая функция Свойства функции
Свойства функции «Повторение – мать учения»
«Повторение – мать учения» Производная функций. Обобщающий урок
Производная функций. Обобщающий урок Применение рядов в приближенных вычислениях. (Тема 14.5)
Применение рядов в приближенных вычислениях. (Тема 14.5) Парная регрессия и корреляция
Парная регрессия и корреляция Задачи
Задачи Презентация на тему Математические головоломки
Презентация на тему Математические головоломки  Числовые множества. Комплексные числа
Числовые множества. Комплексные числа Десятичные дроби. Приложение к уроку в 5 классе
Десятичные дроби. Приложение к уроку в 5 классе Задачи на построение треугольника
Задачи на построение треугольника Математический трамвайчик. Конкурс
Математический трамвайчик. Конкурс Построение треугольника по трем элементам
Построение треугольника по трем элементам Квадратный корень из произведения и дроби
Квадратный корень из произведения и дроби Решение задач на проценты. Подготовка к ГИА
Решение задач на проценты. Подготовка к ГИА Применение ИКТ для повышения качества образования
Применение ИКТ для повышения качества образования Линейная функция и её график (часть I)
Линейная функция и её график (часть I) Определение высоты здания
Определение высоты здания Вычисление длин дуг. Вычисление объемов тел по площадям поперечных сечений. Вычисление объемов тел вращения. (Лекция 10)
Вычисление длин дуг. Вычисление объемов тел по площадям поперечных сечений. Вычисление объемов тел вращения. (Лекция 10)