Содержание
- 2. Понятие числовой функции Переменной величиной будем называть числовую величину, которая в изучаемой задаче принимает различные значения.
- 3. Если каждому числу x ставится в соответствие одно, определенное по правилу f, число – значение числовой
- 8. Замечание: Разность двух функций бесконечно больших при x → a ,имеющих значения одинаковых знаков, неопределена; неопределены
- 9. Замечательные пределы
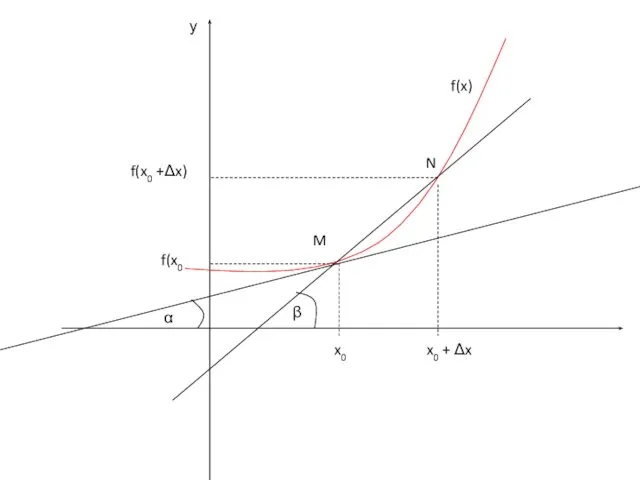
- 12. у f(x0 +Δx) f(x0 α x0 x0 + Δx M f(x) β N
- 13. Пусть f(x) определена на некотором промежутке (a, b). Тогда тангенс угла наклона секущей МР к графику
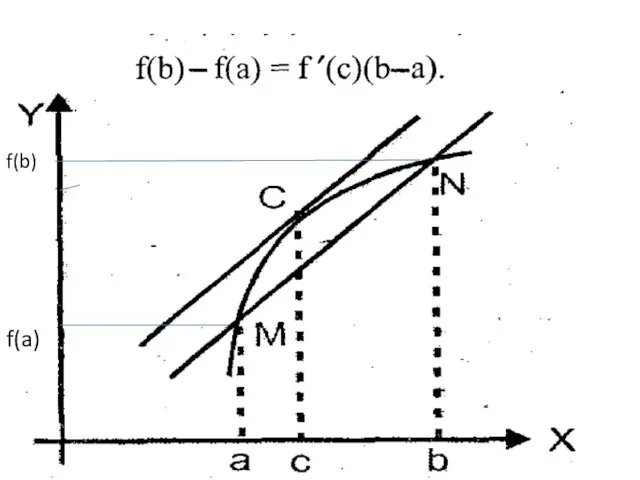
- 14. f(b) f(a)
- 18. Пример. Найти производную функции . Сначала преобразуем данную функцию:
- 22. Интегральное исчисление. Первообразная функция. Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если
- 23. Неопределенный интеграл. Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) +
- 26. Методы интегрирования Непосредственное интегрирование.
- 27. Способ подстановки (замены переменных).
- 28. Интегрирование по частям.
- 30. Определенный интеграл. Пусть на отрезке [a, b] задана непрерывная функция f(x).
- 31. Если для функции f(x) существует предел то функция называется интегрируемой на отрезке [a, b].
- 33. Скачать презентацию
























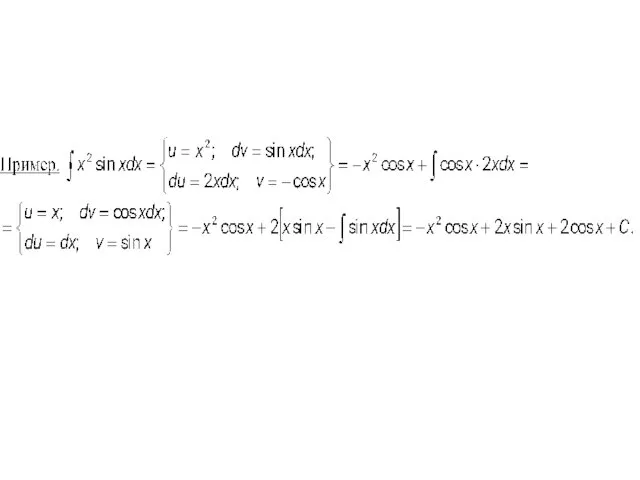
![Определенный интеграл. Пусть на отрезке [a, b] задана непрерывная функция f(x).](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/498128/slide-29.jpg)
![Если для функции f(x) существует предел то функция называется интегрируемой на отрезке [a, b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/498128/slide-30.jpg)
 Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Функция, область определения, значения, четность. Автор: Горбунова В. И., учитель математик
Функция, область определения, значения, четность. Автор: Горбунова В. И., учитель математик Нахождение высоты с помощью шеста
Нахождение высоты с помощью шеста Жай бөлшектерді қосу және азайту
Жай бөлшектерді қосу және азайту Основы финансовых вычислений
Основы финансовых вычислений СУММА УГЛОВ ТРЕУГОЛЬНИКА
СУММА УГЛОВ ТРЕУГОЛЬНИКА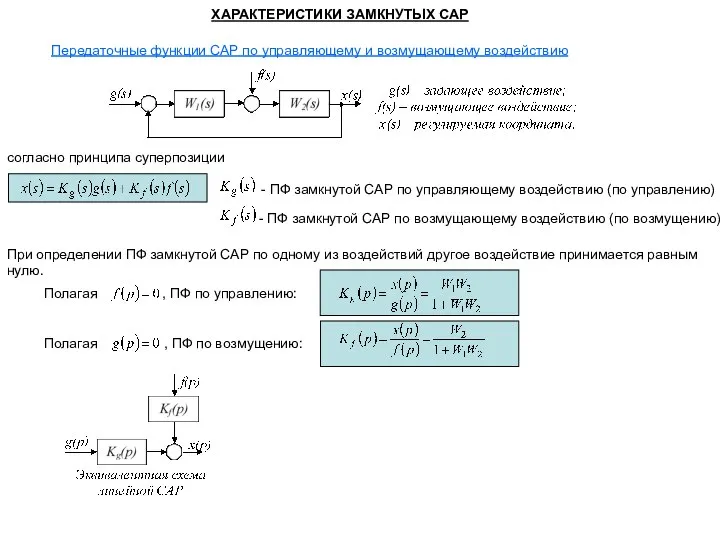 Характеристики замкнутых САР
Характеристики замкнутых САР Признаки параллельности прямых
Признаки параллельности прямых Площадь прямоугольника
Площадь прямоугольника Решение систем уравнений второй степени с двумя переменными методом сложения
Решение систем уравнений второй степени с двумя переменными методом сложения Презентация по математике "Правила сравнения чисел" - скачать бесплатно
Презентация по математике "Правила сравнения чисел" - скачать бесплатно Оболонки додатної і відʼємної Гаусової кривизни
Оболонки додатної і відʼємної Гаусової кривизни Вписанная и описанная окружность
Вписанная и описанная окружность Измерение отрезков
Измерение отрезков Деление с остатком. 5 класс
Деление с остатком. 5 класс Вычитание смешанных чисел
Вычитание смешанных чисел Процентные расчёты
Процентные расчёты Презентация по математике "Пресс - конференция" - скачать
Презентация по математике "Пресс - конференция" - скачать  Отрезок. Прямая. Луч
Отрезок. Прямая. Луч Вписанная и описанная окружности
Вписанная и описанная окружности Понятие площади фигуры и её измерение. Что такое площадь. Свойства площади. Какие фигуры называют равными. Какие фигуры называют
Понятие площади фигуры и её измерение. Что такое площадь. Свойства площади. Какие фигуры называют равными. Какие фигуры называют  Основы математической обработки информации
Основы математической обработки информации Уравнения 5 класс
Уравнения 5 класс Раскрытие скобок
Раскрытие скобок Презентация по математике "Натуральное число 5" - скачать бесплатно
Презентация по математике "Натуральное число 5" - скачать бесплатно Книга природы, написанная языком математики
Книга природы, написанная языком математики Игра на уроке математики (5 класс)
Игра на уроке математики (5 класс) Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения