Содержание
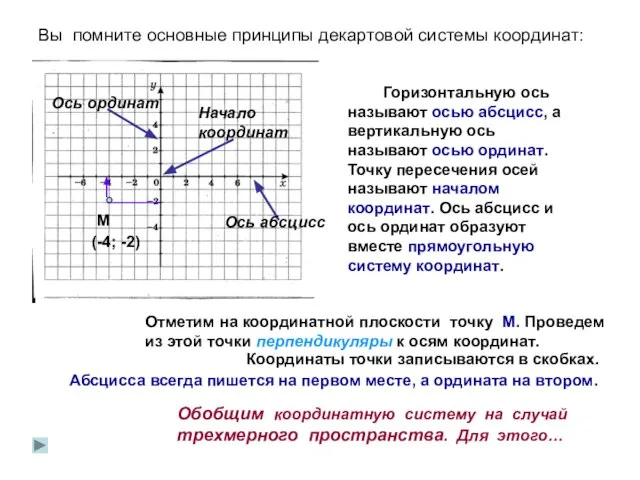
- 2. Вы помните основные принципы декартовой системы координат: Ось абсцисс Ось ординат Начало координат Горизонтальную ось называют
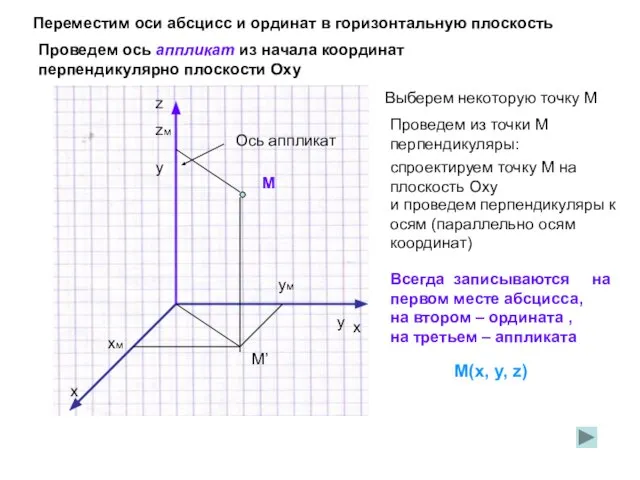
- 3. x x y y z Переместим оси абсцисс и ординат в горизонтальную плоскость Проведем ось аппликат
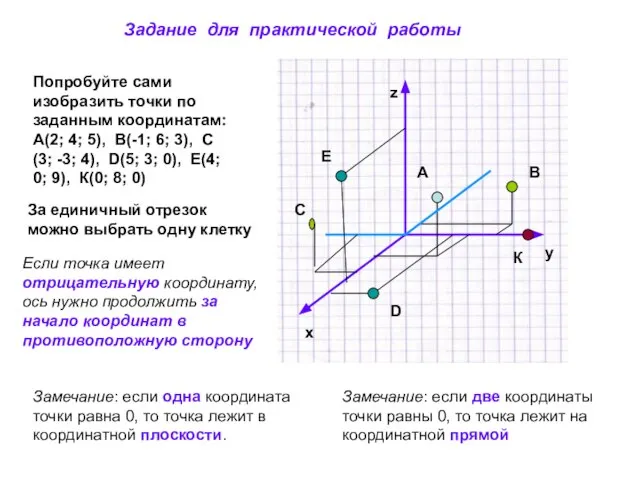
- 4. Замечание: если одна координата точки равна 0, то точка лежит в координатной плоскости. Замечание: если две
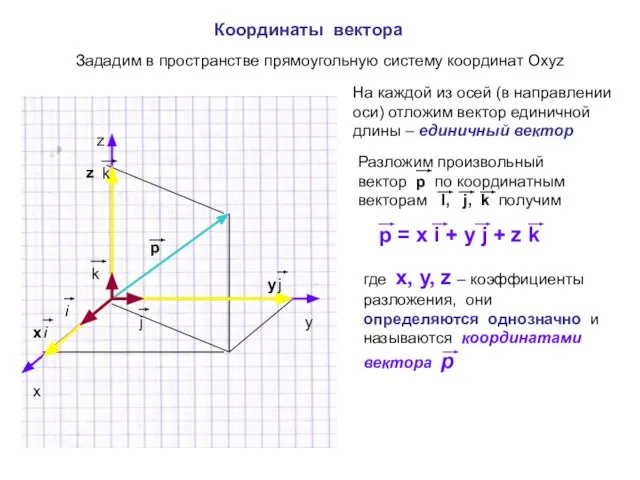
- 5. Координаты вектора Зададим в пространстве прямоугольную систему координат Охуz x y z На каждой из осей
- 6. Действия над векторами, записанными в координатной форме Координаты равных векторов равны Координаты суммы векторов равны суммам
- 7. Действия над векторами, записанными в координатной форме Скалярное произведение векторов Скалярное произведение двух векторов есть число,
- 8. Основные задачи, решаемые в координатах 1. Записать координаты вектора, заданного координатами его концов М О хм
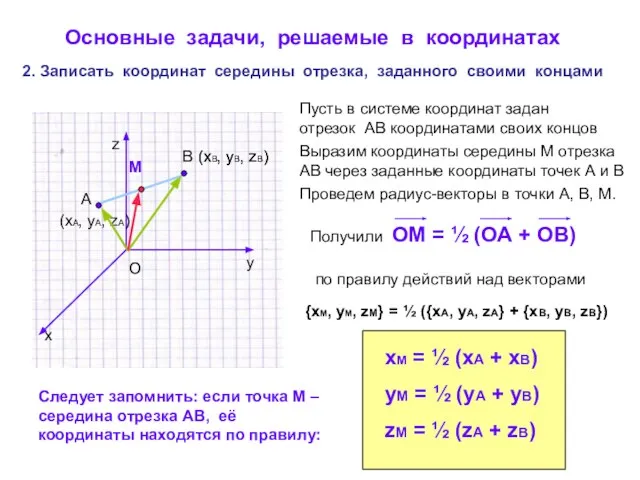
- 9. Основные задачи, решаемые в координатах 2. Записать координат середины отрезка, заданного своими концами A B (xA,
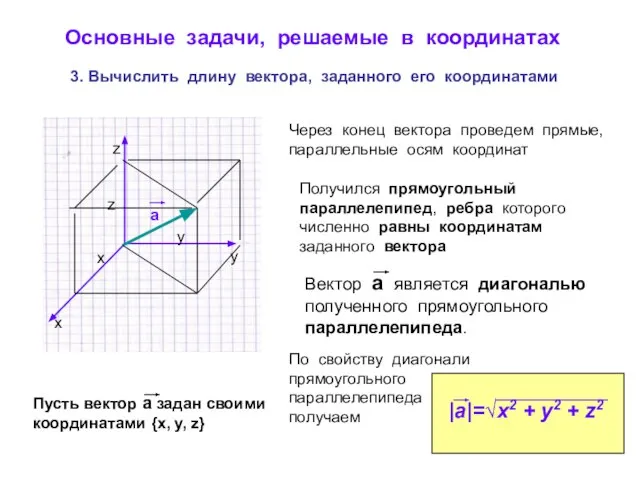
- 10. Основные задачи, решаемые в координатах 3. Вычислить длину вектора, заданного его координатами Через конец вектора проведем
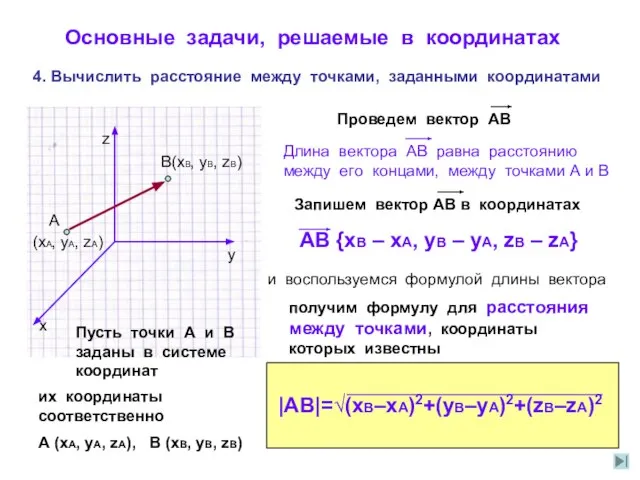
- 11. Основные задачи, решаемые в координатах 4. Вычислить расстояние между точками, заданными координатами А В (xA, yA,
- 12. Основные задачи, решаемые в координатах 5. Найти угол между двумя прямыми, заданными своими направляющими векторами Пусть
- 14. Скачать презентацию




 Описательная статистика. Средние величины
Описательная статистика. Средние величины Презентация____
Презентация____ Сложение и вычитание десятичных дробей. 5 класс
Сложение и вычитание десятичных дробей. 5 класс Аттестационная работа. Методическая разработка по выполнению проекта «Цифры и числа в нашей жизни»
Аттестационная работа. Методическая разработка по выполнению проекта «Цифры и числа в нашей жизни» Построение графика квадратичной функции
Построение графика квадратичной функции Исследование функций в КИМах ЕГЭ (тест по алгебре 10 класс)
Исследование функций в КИМах ЕГЭ (тест по алгебре 10 класс) Угол и луч
Угол и луч Параллель және перпендикулярлы жазықтықтардың ерекшеліктері мен қасиеттері
Параллель және перпендикулярлы жазықтықтардың ерекшеліктері мен қасиеттері Машинная арифметика в рациональных числах
Машинная арифметика в рациональных числах Умножение чисел столбиком
Умножение чисел столбиком Подготовка к контрольной работе по алгебре . 9 класс
Подготовка к контрольной работе по алгебре . 9 класс Тема урока: «Закрепление пройденного материала»
Тема урока: «Закрепление пройденного материала» Множества. Операции над множествами
Множества. Операции над множествами Свойства сложения
Свойства сложения Готовимся к ВПР по математике
Готовимся к ВПР по математике Свойство углов треугольника
Свойство углов треугольника Арифметические действия с десятичными дробями. Математический тренажёр
Арифметические действия с десятичными дробями. Математический тренажёр Презентация по математике "Переместительный закон умножения" - скачать бесплатно
Презентация по математике "Переместительный закон умножения" - скачать бесплатно Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Нужна ли математика в парикмахерской
Нужна ли математика в парикмахерской Автоматизация конструкторско-технологического проектирования
Автоматизация конструкторско-технологического проектирования Функция y = sin x, ее свойства и график
Функция y = sin x, ее свойства и график Презентация Доли. Обыкновенные дроби
Презентация Доли. Обыкновенные дроби Графики функций
Графики функций Своя игра (3)
Своя игра (3) « Н.И.Лобачевский и « Н.И.Лобачевский и проблемы образования» Работа ученика 9 класса МБОУ «оош №12»о.Мурома Ж
« Н.И.Лобачевский и « Н.И.Лобачевский и проблемы образования» Работа ученика 9 класса МБОУ «оош №12»о.Мурома Ж Круглые числа. Счёт десятками. Решение задач. Десять. Уравнения. Величины
Круглые числа. Счёт десятками. Решение задач. Десять. Уравнения. Величины Презентация на тему Число и цифра 7
Презентация на тему Число и цифра 7