Методы численного интегрирования (нахождение определенных интегралов)

1. Аналитический метод

Где F(x) – первообразная функции f(x)

Аналитический метод интегрирования не всегда может быть применен на практике.
Пример «неберущегося»

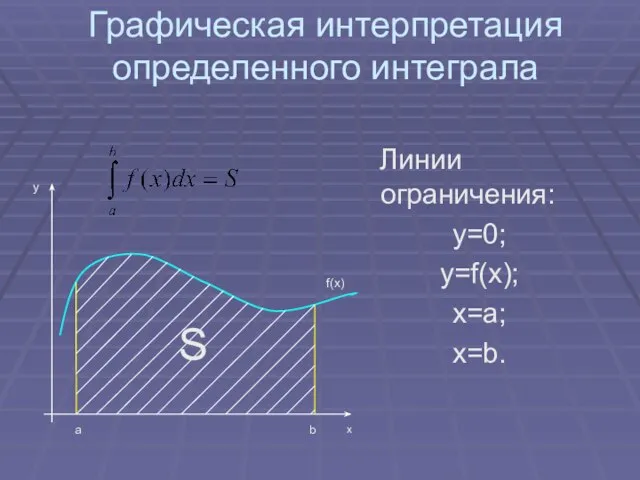
Графическая интерпретация определенного интеграла

Линии ограничения:
y=0;
y=f(x);
x=a;
x=b.

2. Численные методы

1. [a, b] разбивается на n равных отрезков

1. Метод прямоугольников
Отдельно взятая полоса представляется в виде прямоугольника шириной h.
ВОПРОС:

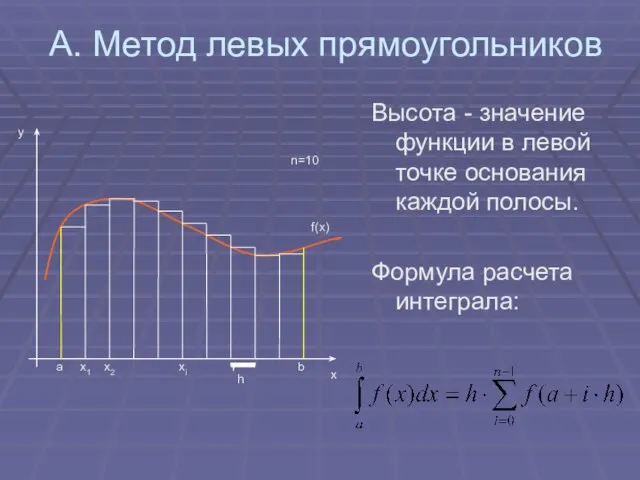
А. Метод левых прямоугольников

Высота - значение функции в левой точке основания

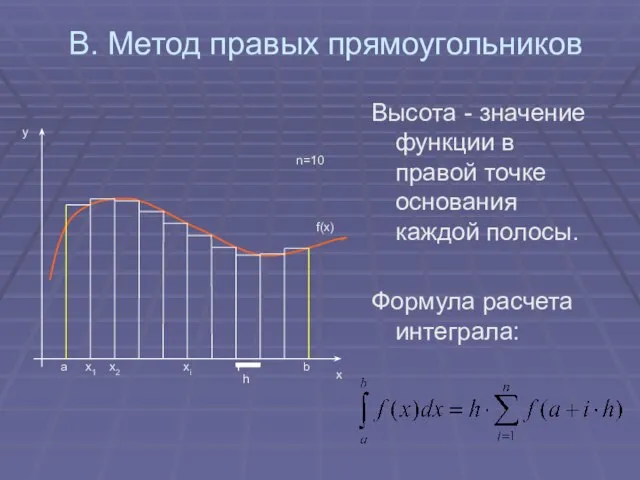
B. Метод правых прямоугольников

Высота - значение функции в правой точке основания

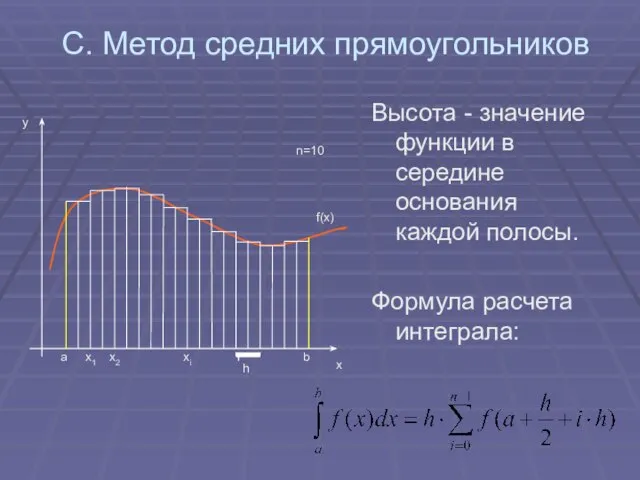
С. Метод средних прямоугольников

Высота - значение функции в середине основания каждой

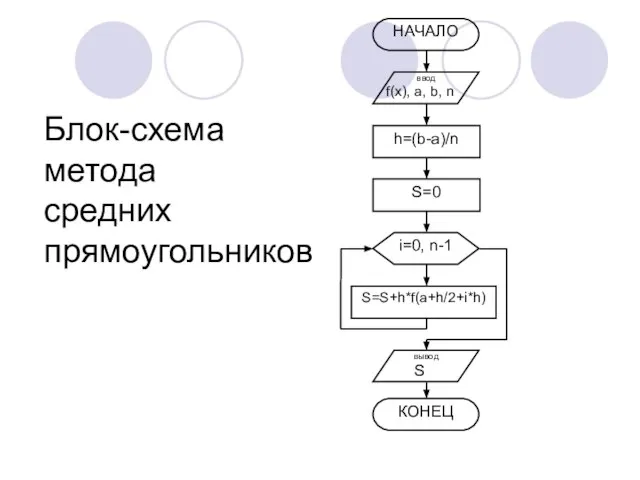
Блок-схема метода средних прямоугольников

2. Метод трапеций

Отдельно взятая полоса представляется в виде перевернутой трапеции высотой

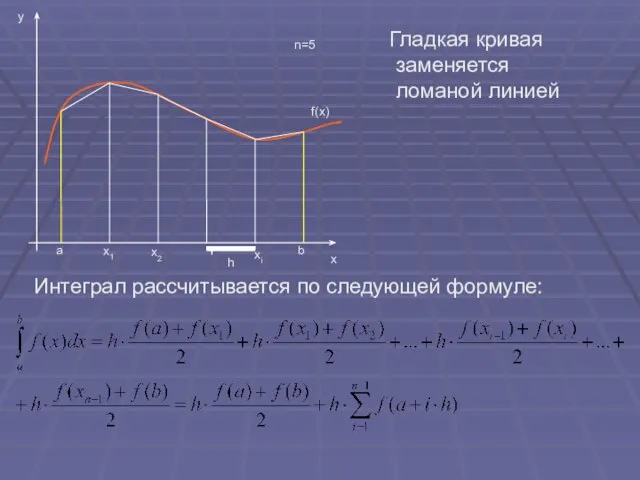
Гладкая кривая заменяется ломаной линией

Интеграл рассчитывается по следующей формуле:

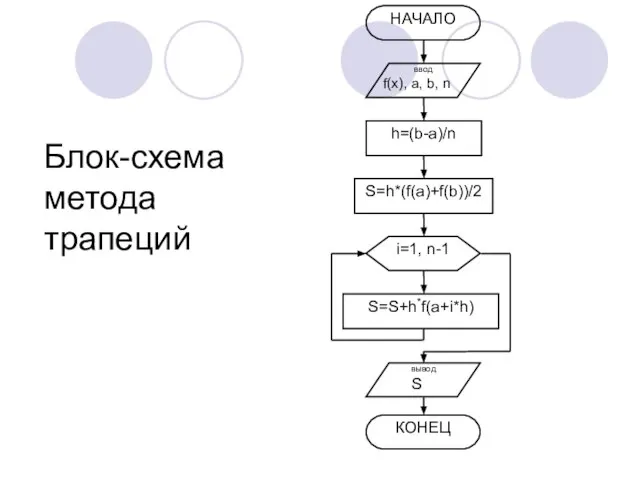
Блок-схема метода трапеций

3. Метод Симпсона

Гладкая функция заменяется участками парабол.
Через любые 3 точки

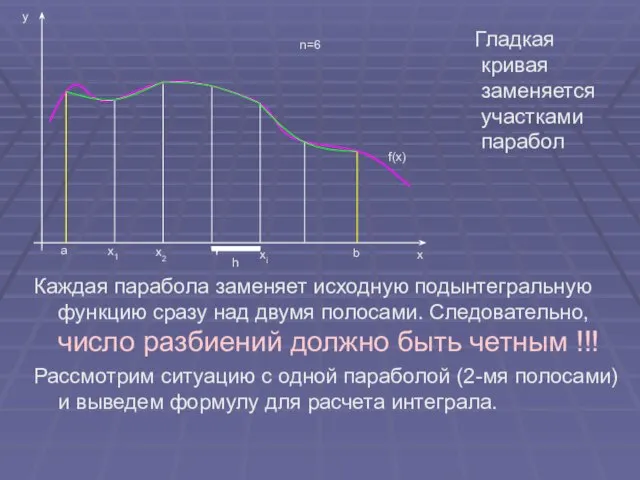
Гладкая кривая заменяется участками парабол

Каждая парабола заменяет исходную подынтегральную функцию

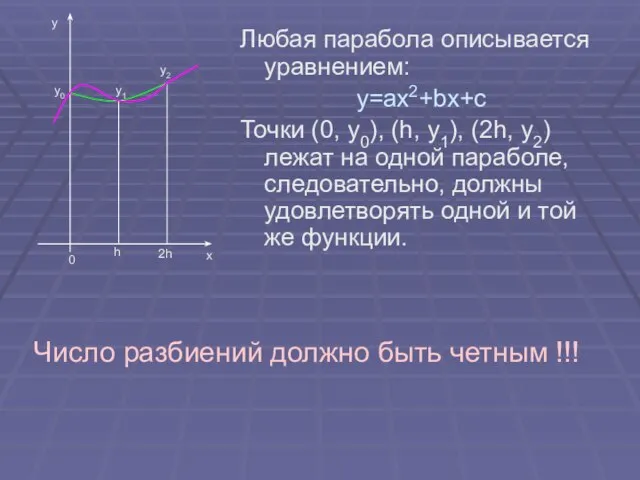
Любая парабола описывается уравнением:
y=ax2+bx+c
Точки (0, y0), (h, y1), (2h, y2) лежат

Подставляем координаты 3-х точек в уравнение для параболы, получаем систему линейных

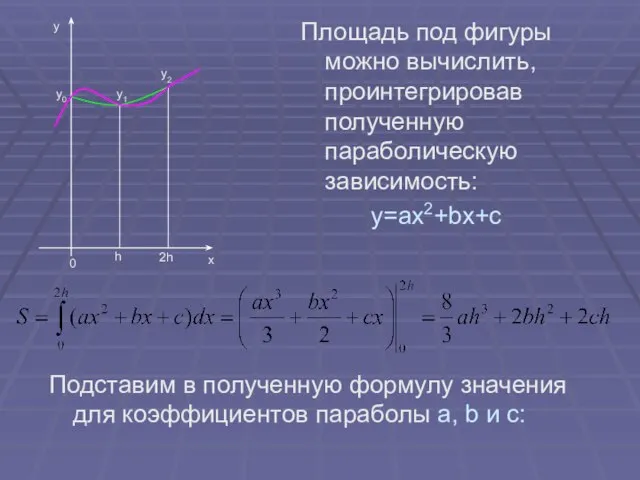
Площадь под фигуры можно вычислить, проинтегрировав полученную параболическую зависимость:
y=ax2+bx+c

Подставим в полученную

Получим:
Если число разбиений будет не 2, а 4, то формула для

В общем виде:
Формула Симпсона

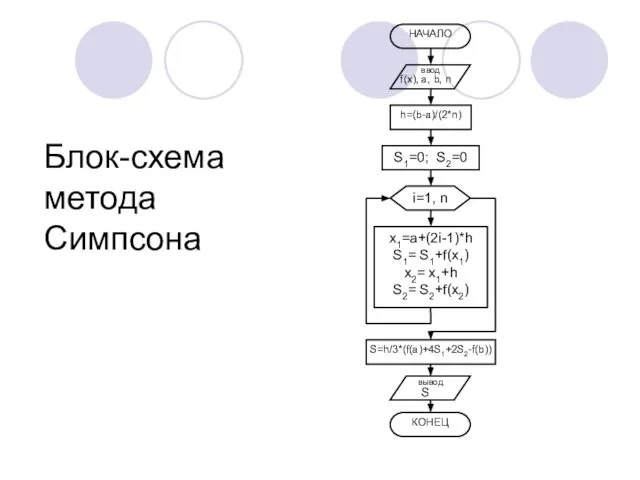
Блок-схема метода Симпсона

Замечания о погрешности численного интегрирования

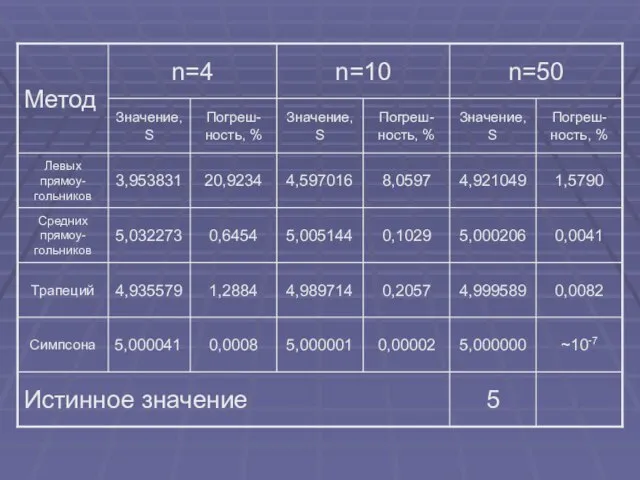
Для оценки погрешности численного интегрирования сравним значения интеграла, рассчитанные различными численными

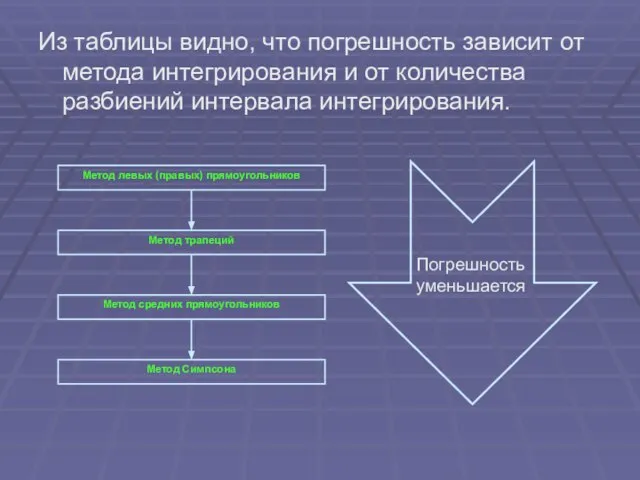
Из таблицы видно, что погрешность зависит от метода интегрирования и от