Содержание
- 2. Метод замены переменной Сущность интегрирования методом замены переменной (способом подстановки) заключается в преобразовании интеграла в интеграл
- 3. Метод замены переменной Найдите следующие интегралы: Решение: Введём подстановку . Дифференцируя, имеем , откуда Подставив в
- 4. Метод замены переменной Найдите следующие интегралы: Решение: Введём подстановку . Дифференцируя, имеем , откуда . Таким
- 5. Метод замены переменной Найдите следующие интегралы: Решение: Введём подстановку . Дифференцируя, имеем , откуда . Таким
- 6. Интегрирование по частям Интегрируя обе части равенства , получим откуда (1) С помощью этой формулы вычисление
- 7. Интегрирование по частям Найдите следующие интегралы: Решение: Пусть тогда т.е. Используя формулу (1), получим: Решение: Пусть
- 8. Интегрирование по частям Задачи для самостоятельной работы:
- 9. Приложения определенного интеграла Определенный интеграл
- 10. Определенный интеграл В декартовой прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми x=a, x=b (a
- 11. Определенный интеграл Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей. Проведем через полученные
- 12. Связь между определенным интегралом и первообразной (Формула Ньютона - Лейбница) Для непрерывной функции где F(x) –
- 13. Основные свойства определенного интеграла
- 14. Основные свойства определенного интеграла
- 15. Геометрический смысл определенного интеграла Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x),
- 16. Геометрический смысл определенного интеграла Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x),
- 17. Геометрический смысл определенного интеграла Замечание: Если функция изменяет знак на промежутке [a;b] , то
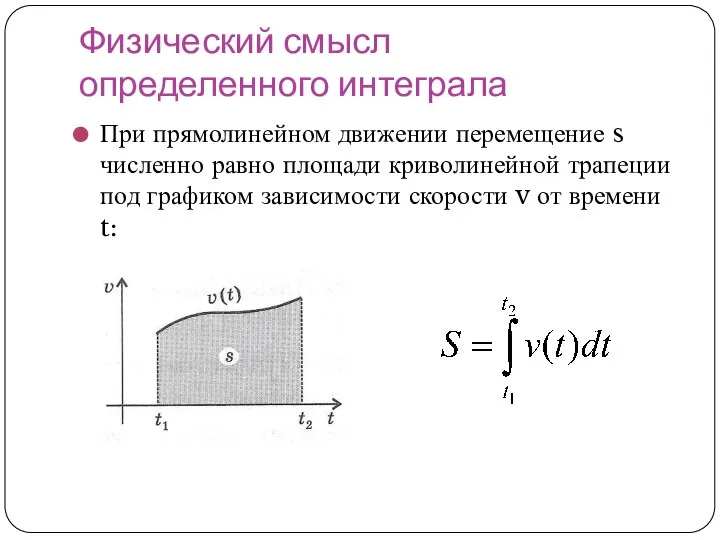
- 18. Физический смысл определенного интеграла При прямолинейном движении перемещение s численно равно площади криволинейной трапеции под графиком
- 19. Пример Вычислить определённый интеграл: = Решение: -2 1
- 20. с помощью определенного интеграла Вычисление площадей и объемов
- 21. Площадь фигуры, Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого x из [a;b],
- 23. Скачать презентацию









![Определенный интеграл Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1445498/slide-10.jpg)





![Геометрический смысл определенного интеграла Замечание: Если функция изменяет знак на промежутке [a;b] , то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1445498/slide-16.jpg)



 Трапеция. Свойства
Трапеция. Свойства Проекция жазықтарын алмастыру әдісі
Проекция жазықтарын алмастыру әдісі Презентация на тему Сложение натуральных чисел и его свойства
Презентация на тему Сложение натуральных чисел и его свойства  Деление десятичных дробей на натуральное число
Деление десятичных дробей на натуральное число Понятие логарифма. Логарифм и его свойства
Понятие логарифма. Логарифм и его свойства Четность, нечетность, периодичность тригонометрических функций
Четность, нечетность, периодичность тригонометрических функций Реляционная алгебра
Реляционная алгебра Методы проверки ответа решенной задачи
Методы проверки ответа решенной задачи Таблица сложения
Таблица сложения Параллелепипед. Призма. Пирамида
Параллелепипед. Призма. Пирамида Числа от 11 до 20
Числа от 11 до 20 Пропорции. Проценты. Диаграммы
Пропорции. Проценты. Диаграммы Властивості прямокутного трикутника
Властивості прямокутного трикутника Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Параллелепипед
Параллелепипед Прямая пропорциональная зависимость
Прямая пропорциональная зависимость Дифференцирование функций комплексной переменной. Понятие аналитической функции
Дифференцирование функций комплексной переменной. Понятие аналитической функции Теорема Ербрана. (Лекция 4)
Теорема Ербрана. (Лекция 4) Презентация на тему Задачи на взвешивание
Презентация на тему Задачи на взвешивание Неделя математики. Открытая неделя - 2020
Неделя математики. Открытая неделя - 2020 Построение линии пересечения цилиндра и конуса
Построение линии пересечения цилиндра и конуса Оформление заданий по математике согласно федеральным образовательным стандартам Программа «школа 2100»
Оформление заданий по математике согласно федеральным образовательным стандартам Программа «школа 2100» Цікавий світ професій
Цікавий світ професій Формулы сокращенного умножения. (Найди ошибку) 7 класс
Формулы сокращенного умножения. (Найди ошибку) 7 класс Контрольно-измерительные инструменты для контроля плоскости
Контрольно-измерительные инструменты для контроля плоскости НОД чисел и НОК чисел
НОД чисел и НОК чисел Золотое сечение
Золотое сечение Розкриття дужок. Зведення подібних доданків
Розкриття дужок. Зведення подібних доданків