Содержание
- 2. Решение нелинейных уравнений Математической моделью многих процессов является функциональная зависимость y = f(x). Одной из задач
- 3. Методы решения делятся на прямые и числен-ные (итерационные). Прямой метод – существует формула для определения значения
- 4. Решение уравнения f(x) = 0 осуществляется в два этапа: 1) приближенное определение местоположе-ния и вид интересующего
- 5. Первая задача может быть решена: 1) на заданном отрезке [a, b] вычисляется таблица значений функции с
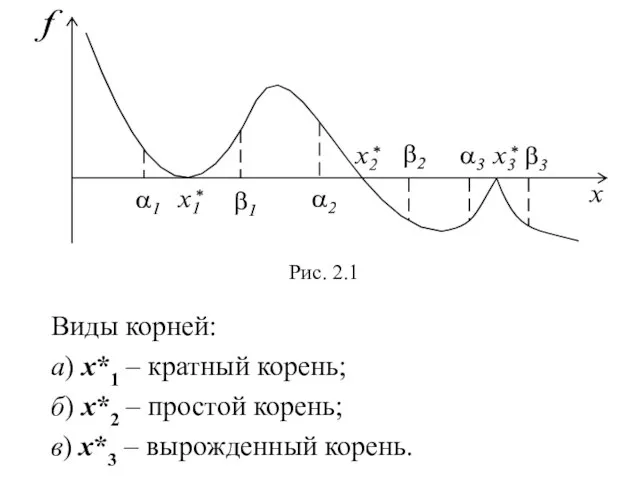
- 6. Виды корней: а) х*1 – кратный корень; б) х*2 – простой корень; в) х*3 – вырожденный
- 7. Для кратного корня (а) : Для простого корня (б) : Для вырожденного корня (в) : не
- 8. Как видно из рисунка 2.1, в случаях a) и в) значение корня совпадает с точкой экстремума
- 9. Метод простой итерации Уравнение f(x) = 0 (1) записывают в разрешен-ном относительно x виде: x =
- 10. Исходя из (2) члены рекуррентной последо-вательности вычисляются по формуле xk = ϕ (xk − 1) ,
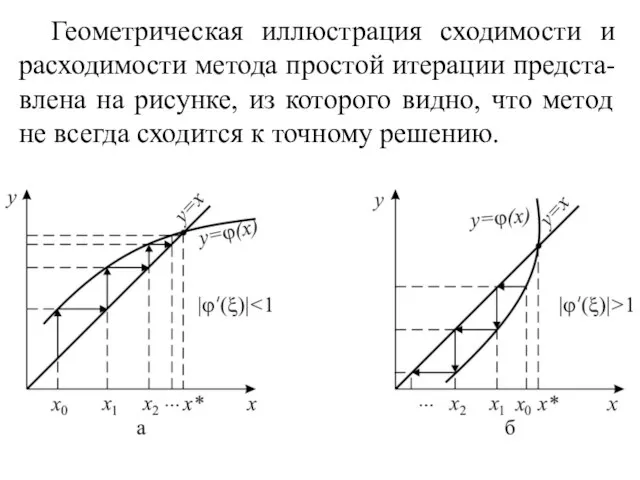
- 11. Геометрическая иллюстрация сходимости и расходимости метода простой итерации предста-влена на рисунке, из которого видно, что метод
- 12. Условия сходимости метода простой итера-ции: 1) ϕ (x) − дифференцируема; 2) выполняется неравенство | ϕ'(ξ) |
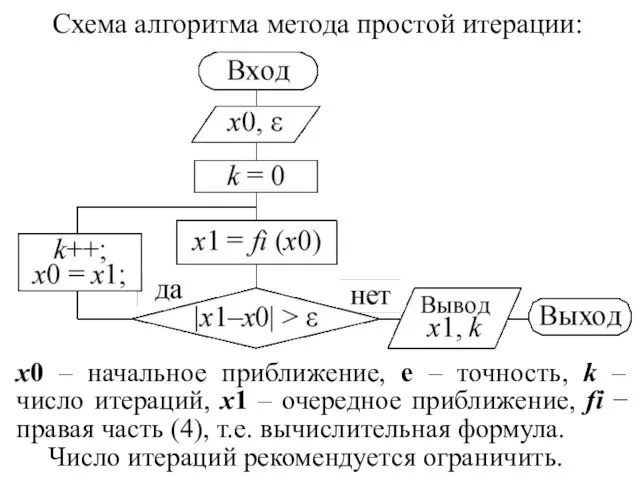
- 13. x0 – начальное приближение, е – точность, k – число итераций, x1 – очередное приближение, fi
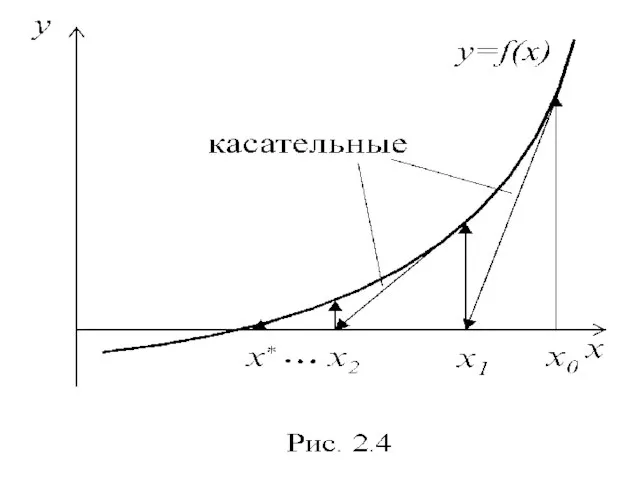
- 14. Метод Ньютона Этот метод − модификация метода простой итерации. Если f(x) имеет непрерывную произво-дную и f(x)
- 15. Метод одношаговый (m = 1), т.к. для начала вычислений требуется задать одно начальное приближение x0 из
- 17. Метод секущих Это модификация метода Ньютона, позволяю-щая избавиться от вычисления производной пу-тем ее замены приближенной формулой,
- 18. Метод одношаговый (m = 1) и его условие сходимости при правильном выборе h такое же, как
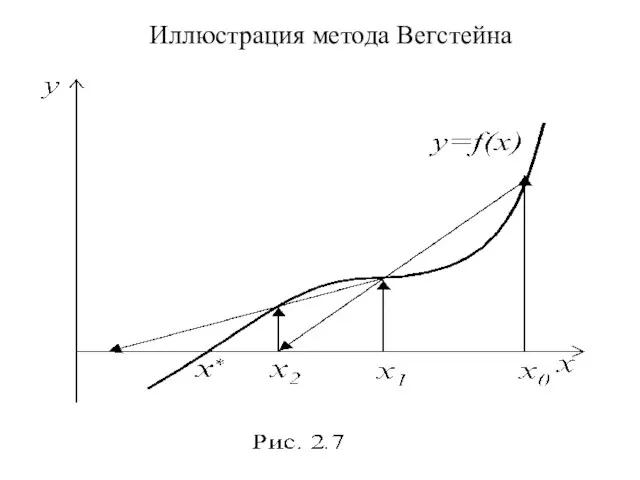
- 19. Метод Вегстейна Этот метод – модификация метода секущих. В нем при расчете приближенного значения произ-водной используется
- 20. Метод двухшаговый (m = 2), т. к. для начала вычислений требуется задать 2 начальных при-ближения. Обычно
- 21. Иллюстрация метода Вегстейна
- 22. Метод деления отрезка пополам Его алгоритм основан на построении рекур-рентной последовательности по следующему правилу: 1) в
- 23. Алгоритм поиска всех простых корней 1. Начало цикла для x, изменяющегося от a до b с
- 24. Алгоритм поиска особых корней 1. Начало цикла для x, изменяющегося от a до b с шагом
- 25. Рассмотрим часть кода для поиска всех про-стых корней на отрезке [a, b]: . . . for
- 26. В предложенном коде объявляются: 1) тип указателя на функцию type_f, исполь-зующийся в функции Metod в качестве
- 27. Метод деления отрезка пополам Прототип функции имеет следующий вид: double Metod (type_f, double, double, double); первый
- 29. Скачать презентацию



![Первая задача может быть решена: 1) на заданном отрезке [a, b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/619395/slide-4.jpg)

















 Биостатистика. Сравнение выборок
Биостатистика. Сравнение выборок Презентация на тему: Длина
Презентация на тему: Длина Параллельный перенос
Параллельный перенос Нахождение дроби и процентов от числа
Нахождение дроби и процентов от числа Геометрические характеристики плоских сечений
Геометрические характеристики плоских сечений Презентация по математике Отношения и пропорции
Презентация по математике Отношения и пропорции  Статистический анализ данных
Статистический анализ данных Аттестационная работа. Создание творческого проекта «Задачи на движение»
Аттестационная работа. Создание творческого проекта «Задачи на движение» Окружность вписанная и описанная
Окружность вписанная и описанная Презентация по математике "Прямая и обратная пропорциональные зависимости" - скачать бесплатно
Презентация по математике "Прямая и обратная пропорциональные зависимости" - скачать бесплатно Многоугольники. Пентамино
Многоугольники. Пентамино Подготовка к ОГЭ. Методы, способствующие решению геометрических задач
Подготовка к ОГЭ. Методы, способствующие решению геометрических задач Уравнение окружности и прямой
Уравнение окружности и прямой Графики линейной функции, содержащей модуль
Графики линейной функции, содержащей модуль Треугольник и его виды
Треугольник и его виды Подготовка к ВПР (№1). Математика 6 класс
Подготовка к ВПР (№1). Математика 6 класс Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Презентация на тему Математический диктант 1 класс
Презентация на тему Математический диктант 1 класс  «Золотое сечение» (виртуальный факультатив)
«Золотое сечение» (виртуальный факультатив) Стереометрия 2 часть. Подготовка к ЕГЭ по математике 2019
Стереометрия 2 часть. Подготовка к ЕГЭ по математике 2019 Буквенная запись свойств сложения и вычитания
Буквенная запись свойств сложения и вычитания Вычислительные навыки на уроках математики
Вычислительные навыки на уроках математики Из истории возникновения теории вероятностей
Из истории возникновения теории вероятностей Лабиринты Выполнили: Трунцова Кристина и Морозова Мария Руководитель проекта: Кондрашова Елена Анатольевна
Лабиринты Выполнили: Трунцова Кристина и Морозова Мария Руководитель проекта: Кондрашова Елена Анатольевна  Наибольший общий делитель. Нахождение НОД. учитель математики Фролова Мария Викторовна МКОУ СОШ № 26 с. Мельничное Красноарм
Наибольший общий делитель. Нахождение НОД. учитель математики Фролова Мария Викторовна МКОУ СОШ № 26 с. Мельничное Красноарм Применение интегралов в решении задач
Применение интегралов в решении задач Расстояние между точками
Расстояние между точками Определение арифметической прогрессии
Определение арифметической прогрессии